哈夫曼树
1.概念
路径:点到点过程中,经过的所有点;
路径长度:点到点过程中,经过的边数量;
结点的带权路径长度:结点的权重值 × 根到该结点的路径长度;
树的带权路径长度:所有结点的带权路径长度之和。
2.定义
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
3.如何构建哈夫曼树
给出结点[2,3,7,9,18,25],构建哈夫曼树
- 将要构建的结点存储在优先队列中,小的元素先出队;
- 取队头的两个元素作为左右叶子结点构建一颗二叉树,左结点<右结点,父结点=左结点+右结点;
- 取队头的一个元素作为子结点 与 上一步生成的父结点 构建新的二叉树;循环此操作,直到优先队列中没有元素;
- 最后生成一颗哈夫曼树,紫色结点是原来的结点,蓝色是新生成的结点,时间复杂度O(nlog2n),空间复杂度O(n)
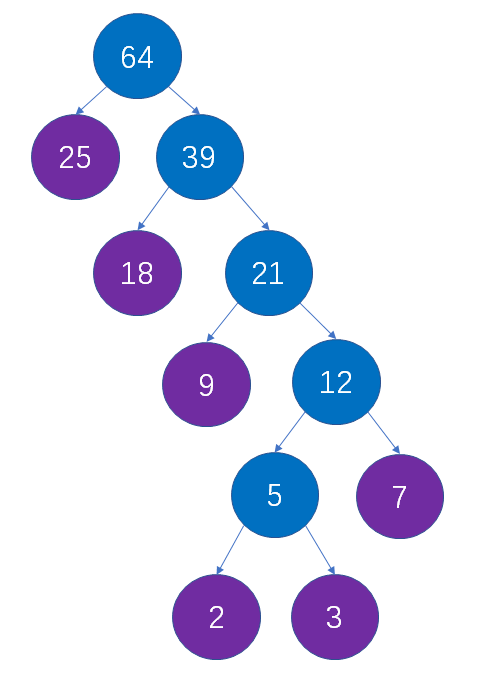
4.哈夫曼编码
这是一种高效的编码方式,在信息存储和传输过程中,用于对信息进行压缩,不是等长编码,但保证平均编码长度最小。
对比ASCII编码方式,就是把每一个字符表示成特定的8位二进制,等长编码。
哈夫曼编码是根据字符出现的次数或者频率来编码的,例如字母[A,B,C,D,E,F]分别出现了[2,3,7,9,18,25],则可以得到这样的哈夫曼树:
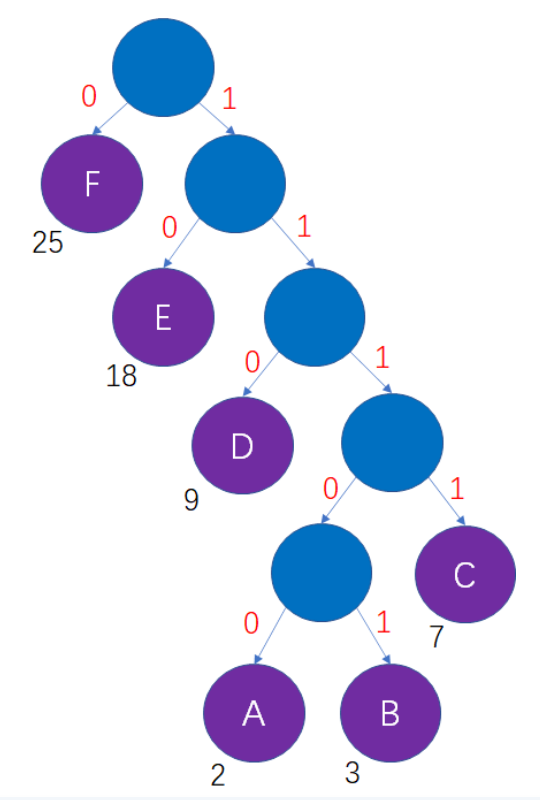
从根结点往左走编码为0,往右编码为1,保证字符在叶子结点,不会有前缀冲突,可以得到这样的编码
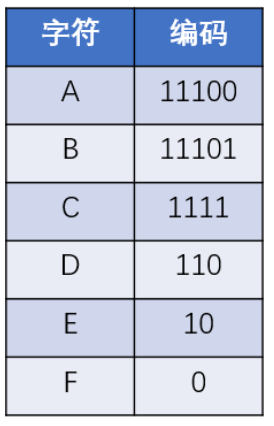
哈夫曼编码长度 = 5×2 + 5×3 + 4×7 + 3×9 + 2×18 + 1×25 = 141
6个字符用等长编码至少需要三位二进制。
定长编码长度 = 3×(2+3+7+9+18+25) = 192
结点权重 = 字符频次,路径长度 = 编码长度,树的带权路径长度 = 总编码长度 最小。
参考&引用
https://baijiahao.baidu.com/s?id=1663514710675419737&wfr=spider&for=pc



