NC51180—Accumulation Degree—(换根dp)
https://ac.nowcoder.com/acm/problem/51180
题意:有一棵n个节点的树,边上有流量限制,根节点发出流量流向叶子节点。求哪个点作为根节点时,流向叶子节点的总量最多。n<=200000
思路:
边上会限流,像网络流的最大流,但只是树,比较好解一点。暴力解法枚举根节点时间复杂度O(n2)直接gg。变换根节点,用所谓的换根dp。
解法基本都是从dfs考虑,从上往下还是从下往上。
很容易想到,如果从上往下的话,分流时还没有考虑到下面的边权值,不好分流,万一分了很多流量给某个节点,结果它连着叶子节点那条边权值为1,那就亏大了。
那就是从下往上计算,可以知道,叶子节点的父亲能 发送到叶子节点的流量和 是 连着叶子节点的边 的权值和。 叶子节点的父亲再往上返回给爷爷的话,需要受到 边流量的影响。有dp[i]表示以i节点为根的子树能 流到 叶子节点的流量总和。子树根节点为u,对于儿子v有两种情况。
v是叶子节点,dp[u]+=flow[u][v]。v不是叶子节点,dp[u]+=min(dp[v],flow[u][v]),边起到限流作用,需要取小。
一开始以1为根跑一边树形dp确定dp数组,这是固定一个根节点求出的子树最大流量。
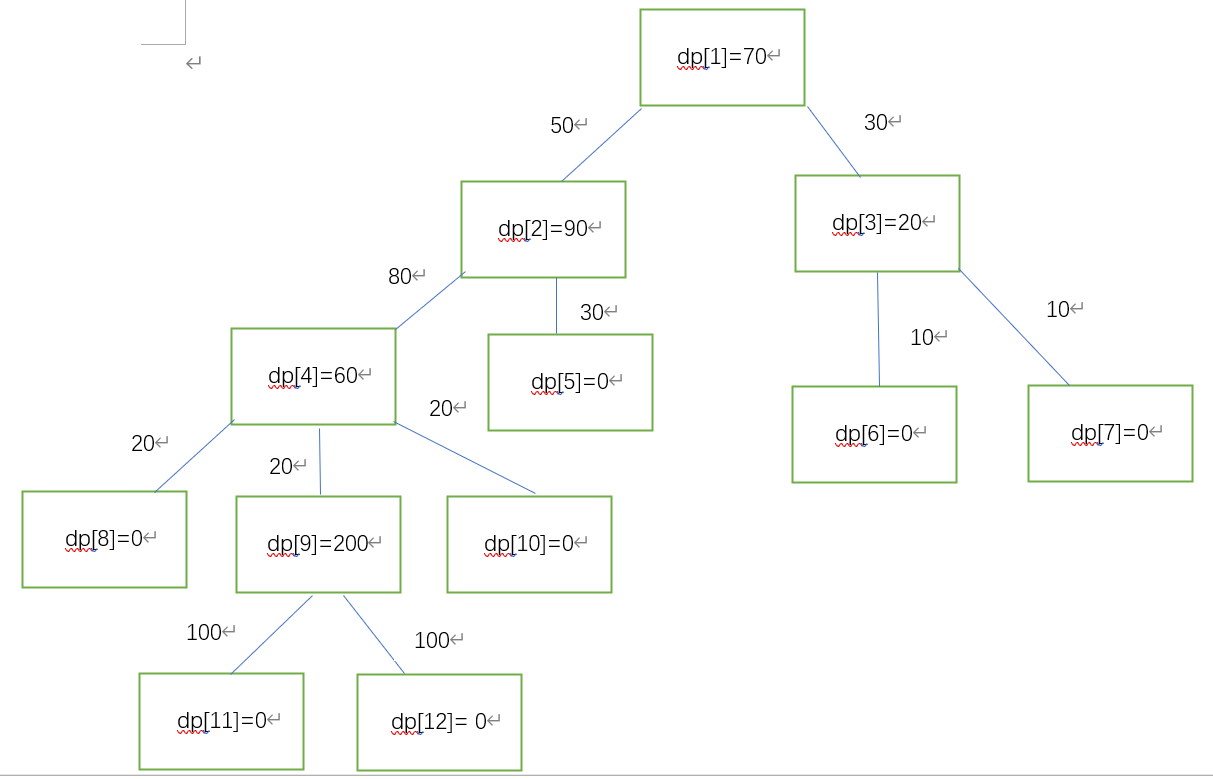
从图可以很清晰地看到,如果以2作为根,它的答案就是dp[2]+能流向1的最大流量。如果以4作为根节点,答案就是dp[4]+能流向2的最大流量。对于父节点u和子节点v,进行换根操作。有ans[v] = dp[v] + min( ans[u]-min( dp[v],flow[u][v] ),flow[u][v] );又一个dfs,对于第ans[u]而不是dp[u],因为要确定 以u为根节点的流量是正确答案,这样才能和dp[v]相操作得到 v的答案。而dfs能求出ans[root=1]和所有dp[v],作为满足第2次dfs的前提。特判根节点1变成叶子,否则如果是下面这种情况,ans[2]=dp[2]+min(ans[1]-min(dp[2],flow[1][2]),flow[1][2])=13+min(11-11,11)=13。但显然正确的ans[2]=11+23=24。所以这种根节点1被反当成叶子的特判答案是ans[v]=dp[v]+flow[u][v]。
第2次dfs也从1出发,为了确保dfs过程中转台转移方程中的ans[u]能确定,所以是先写dp方程再dfs。

#include<stdio.h> #include<iostream> #include<algorithm> #include<cstring> #include<math.h> #include<string> #include<map> #include<queue> #include<stack> #include<vector> #include<set> #define ll long long #define inf 0x3f3f3f3f using namespace std; struct Edge { int to; int next; int val; }; Edge edge[400005]; int head[200005]; int deg[200005];///入度为1的点就是叶子节点,除了根节点1之外 int dp[200005];///以自己为根节点 能流给 int ans[200005]; int t,n,cnt; void add(int u,int v,int val) { edge[cnt].to=v; edge[cnt].val=val; edge[cnt].next=head[u]; head[u]=cnt++; } ///初始默认1为根,跑一次dfs,dp[i]表示以i为根节点的树 到达i的叶子节点 的总流量最大值,自然dp[叶子]=0 ///节点u对于非叶子节点的儿子v,dp[u]+=min(flow[v],edge[i].val);二者之间的边权值限制 ///对于叶子节点的儿子v,dp[u]+=dp[v] void dfs1(int u,int f) { for(int i=head[u];i!=-1;i=edge[i].next) { int v=edge[i].to; int val=edge[i].val; if(v==f) continue; dfs1(v,u); if(deg[v]==1) dp[u]+=val; else dp[u]+=min(val,dp[v]); } } void dfs2(int u,int f) { for(int i=head[u];i!=-1;i=edge[i].next) { int v=edge[i].to; int val=edge[i].val; if(v==f) continue; if(deg[u]==1)///特判1是叶子的时候 { ans[v]=dp[v]+edge[i].val; } else ///换根,把根换为u的儿子v ans[v]=dp[v]+min( ans[u]-min(dp[v],val),val ); dfs2(v,u); } } int main() { scanf("%d",&t); while(t--) { cnt=0; memset(edge,0,sizeof(edge)); memset(head,-1,sizeof(head)); memset(dp,0,sizeof(dp)); memset(deg,0,sizeof(deg)); memset(ans,0,sizeof(ans)); scanf("%d",&n); for(int i=1;i<n;i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); add(x,y,z); add(y,x,z); deg[x]++; deg[y]++; } dfs1(1,-1); ans[1]=dp[1]; dfs2(1,-1); int maxx=0; for(int i=1;i<=n;i++) maxx=max(ans[i],maxx); printf("%d\n",maxx); } return 0; } /** 1 12 1 2 50 1 3 30 2 4 80 2 5 30 3 6 10 3 7 10 4 8 20 4 9 20 4 10 20 9 11 100 9 12 100 */



