CF1003E-Tree Constructing-(构造+dfs)

https://vjudge.net/problem/CodeForces-1003E

题意：给n个点，构造一棵树，树的直径是d，每个点连接的点数(度数)不超过k。输出构造这棵树的n-1条边。

思路：先构造出一条直径d，再从直径上的点用dfs去延申。

举例n=12，d=5，k=4。

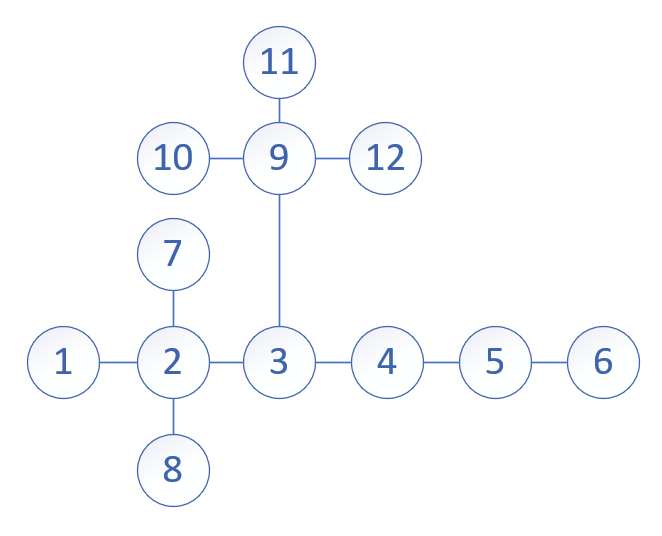
先造出直径1-2-3-4-5-6。对于1和6是直径的两端，显然不能再添加点，否则会使直径变长，所以对2至5这4个点用dfs进行连边操作。dfs的参数为：当前遍历到的点u，当前点还能连的点的个数(度数)deg，还能连接的链的长度dep。dfs中的条件使：后面的点还没用完 并且 该点还可以连接点(度数没达到k) 并且 该点的直径没达到d。每连上一个点继续往深处搜索并且连点同时注意修改deg和dep。如图，从2开始深搜，由于直径长度，连上7后不能继续深搜，而到了3连上9，三个条件允许的情况下又连了10，11，12。

特判：点数<=直径长度 或 度数为1(直径都造不出来)

import java.lang.reflect.Method;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

public class Main{
    
    static Edge[] edge=new Edge[400005];
    static int cnt=0;//边数
    static int [] head=new int[400005];
    static int n,d,k;//点数，直径，最大度数
    static int num=0;//后期搜索过程需要的连上的节点名
    public static void main( String[] args ){
        Scanner scan=new Scanner(System.in);
        while(scan.hasNext()) {
            Arrays.fill(head, 0);
            n=scan.nextInt();
            d=scan.nextInt();
            k=scan.nextInt();
            cnt=1;
            
            if(n<=d || (k==1 && n>2)) {//点数小于等于直径 或 深度不允许
                System.out.println("NO");
                continue;
            }
            
            //先连一条直径为d的边,1-2-3-4-5-...-d-(d+1)
            for(int i=1;i<=d;i++) 
                add_edge(i, i+1);
            
            num = d+1;//dfs中每次+1
            
            for(int i=2;i<=d;i++) 
                dfs(i,k-2,Math.min(i-1, d+1-i));//2到d这些点是一条直线，需要连到d+2,d+3那些点
            
            
            if(num!=n) {
                System.out.println("NO");
                continue;
            }
            System.out.println("YES");
            for(int i=1;i<=n;i++) {
                for(int j=head[i];j!=0;j=edge[j].next)
                    System.out.println(i+" "+edge[j].to);
            }
        }
    }
    public static void add_edge(int u,int v) {//链式前向星添加边
        Edge e=new Edge();
        e.next=head[u];
        e.to=v;
        edge[cnt]=e;
        head[u]=cnt;
        cnt++;
    }
    public static void dfs(int u,int deg,int dep) {//u是当前节点，还能连接deg个新节点，还能连接长度为dep的链
        if(num==n || deg==0 || dep==0)
            return;
        for(int i=0;i<deg && num<n;i++) {
            num++;
            add_edge(u, num);
            dfs(num,k-1,dep-1);
        }
    }
}

class Edge{
    int to;
    int next;
    
}

 天上不会掉馅饼，努力奋斗才能梦想成真。