斐波那契和矩阵快速幂

快速幂

用于对底数的高次幂求模，例如a32常规运算是a连乘32次，快速幂则计算a²，随后计算a⁴，a⁸，a¹⁶，a³²，只运算了5次，贼快。

ll power(ll a,ll b,ll q)
{
    ll res=1;
    while(b)
    {
        if(b%2)
            res=res*a%q;
        b=b/2;
        a=a*a%q;
    }
    return res%q;
}

 

---

矩阵快速幂

1.矩阵相乘

前者行*后者列。结果矩阵的行列分别是前者行数，后者列数。（既然是幂次方，必然是一个n×n的矩阵）

例如：矩阵A是n×p的矩阵，矩阵B为p×m的矩阵，这样A和B才能相乘，结果是矩阵C，C的维度是n×m。

C的计算公式：

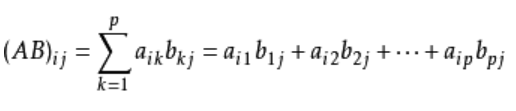
举例说明：

2.矩阵快速幂和数字快速幂一样，只是每一次矩阵相乘都需要三重循环，看起来挺吓人的，耐心看个5min其实也是能懂的。

P3390:n阶矩阵快速幂全裸，java只能过90分？（不知道有没有改进的余地，请大佬赐教）

import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;

public class Main{        //P3390【模板】矩阵快速幂
    
    static long [] [] a=new long [105][105];
    static long [] [] e=new long [105][105];//单位矩阵
    static long p=1000000007;
    static int n;
    static long k;
    public static void main(String []args) {
        //Scanner scan=new Scanner(new BufferedInputStream(System.in));
        Scanner scan=new Scanner( System.in);
        n=scan.nextInt();
        k=scan.nextLong();
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                a[i][j]=scan.nextLong();
        for(int i=1;i<=n;i++)
            e[i][i]=1;
        long [][] ans=pow(a, k);
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=n;j++)
                System.out.print(ans[i][j]+" ");
            System.out.println();
        }
        
    }
    
    public static long[][] mul(long[][] x,long [][] y){//n阶矩阵相乘
        long [] [] c=new long [105][105];
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                c[i][j]=0;
        //对于c矩阵的结果，是x的列与y的行相乘的结果，使用X的列数作为k，必然对应Y的行
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                for(int k=1;k<=n;k++)
                    c[i][j]=(c[i][j]+x[i][k]*y[k][j])%p;
        return c;
    }
    
    public static long[][] pow(long[][] x,long k ){
        long [] [] res=e;//单位矩阵
        while(k!=0) {
            if(k%2==1)
                res=mul(res,x);
            x=mul(x, x);
            k=k/2;
        }
        return res;
    }
}

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<math.h>
#include<string>
#include<map>
#include<queue>
#include<stack>
#include<set>
#include<ctime>
#define ll long long
#define inf 0x3f3f3f3f
const double pi=3.1415926;
using namespace std;

struct matrix{
    ll x[105][105];
};
matrix a,e;
int n;
ll p=1000000007;
ll b;


matrix mul(matrix a,matrix b){
    matrix res;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
        res.x[i][j]=0;//初始化清0操作
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
        for(int k=1;k<=n;k++)
          res.x[i][j]=(res.x[i][j]+a.x[i][k]*b.x[k][j]  )%p;
    return res;
}

matrix pow( matrix a,ll b)
{
    matrix res=e;
    while(b){
        if(b%2==1)
            res=mul(res,a);
        b=b/2;
        a=mul(a,a);
    }
    return res;

}


int main()//P3390
{
    scanf("%d %lld",&n,&b);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        scanf("%lld",&a.x[i][j]);
    for(int i=1;i<=n;i++)
        e.x[i][i]=1;

    matrix ans=pow(a,b);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
            printf("%lld ",ans.x[i][j]);
        printf("\n");
    }

    return 0;
}

 

---

 斐波那契矩阵快速幂 

1.斐波那契数列递推式 f(n)=f(n-1)+f(n-2)

默认第一项为0,f(0)=0;f(1)=1;f(2)=1;f(3)=2;f(4)=3;f(5)=5;f(6)=8;...

2.融合进矩阵运算公式

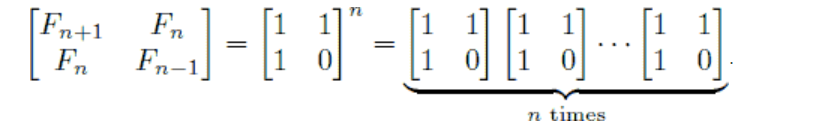
底数矩阵为[  f(2),f(1);f(1),f(0)  ];n次幂后取矩阵A_n右上角的数为f(n)

手动验证一下[ 1,1; 1,0 ]*A_n = [ 1,1; 1,0 ]*[ f(n+1),f(n); f(n),f(n-1) ] = [ f(n+1)+f(n),f(n)+f(n-1); f(n+1),f(n) ] = [ f(n+2),f(n+1); f(n+1),f(n) ];

---

 

斐波那契求前n项平方和

公式和图证如下：

 

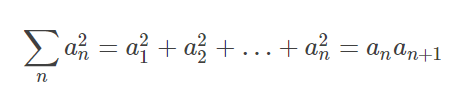
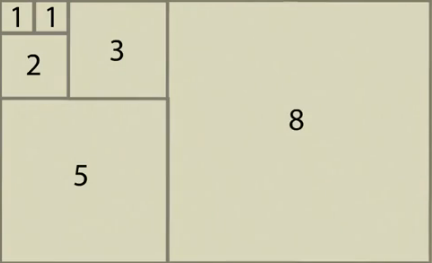
题目：https://ac.nowcoder.com/acm/contest/3282/A，套用斐波那契矩阵快速幂的模板。

import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;

public class Main{    
    
    static long[][] a=new long[3][3];//底数矩阵
    static long[][] e=new long[3][3];//单位矩阵
    static long p=1000000007;
    public static void main(String []args) {
        //Scanner scan=new Scanner(new BufferedInputStream(System.in));
        Scanner scan=new Scanner( System.in);
        a[1][1]=1;a[1][2]=1;a[2][1]=1;a[2][2]=0;
        e[1][1]=e[2][2]=1;
        long k=scan.nextLong();
        long[][] res=pow(a, k);
        long ans=res[1][1]*res[1][2]%p;
        System.out.println(ans);
        
    }
    
    public static long[][] mul(long[][] x,long [][] y){//n阶矩阵相乘
        long [] [] c=new long [3][3];
        for(int i=1;i<=2;i++)
            for(int j=1;j<=2;j++)
                for(int k=1;k<=2;k++)
                    c[i][j]=(c[i][j]+x[i][k]*y[k][j])%p;
        return c;
    }
    public static long[][] pow(long[][] x,long k ){
        long [] [] res=e;//单位矩阵
        while(k!=0) {
            if(k%2==1)
                res=mul(res,x);
            x=mul(x, x);
            k=k/2;
        }
        return res;
    }

}

 

 

---

 

斐波那契循环节

求斐波那契数列模N意义下的循环节

1.唯一分解定理

定义：任何一个数N可以表示成 素数的次方 的乘积

分解公式： 

求N的因子个数公式：num=(a₁+1)×(a₂+1)×......×(a_n+1);

2.分别计算Fib数列每个p^m的循环节长度，假设长度为L(p^m),用L(p)表示斐波那契数列模p意义下的循环节

有一个定理：L(p^m)=L(p) × p^m-1 

 

未完待补，二次剩余实在是看不下去了。。。