计算机的各种码

在计算机中，数据一律是用二进制补码来存储。

符号位：二进制左边第1位，1表示负，0表示正

有3种码，原码、反码和补码。

正数：原码=反码=补码

负数：反码=原码除符号位其他全部取反，补码=反码+1

正数就不举例了，举例负数-1

原码：1000 0001

反码：1111 1110，除符号位(左边第一位)外其他取反

补码：1111 1111，反码+1。

二进制补码转为十进制，我的计算方法是：-2⁸+2⁷+2⁶+2⁵+2⁴+2³+2²+2¹+2⁰=-128+64+32+16+8+4+2+1=-1

原码反码补码计算器：http://www.atoolbox.net/Tool.php?Id=952

---

 暂且认为以上是对的，但是对于转型就有些争议了。

看到很多博客对转型说法各不相同，虽然字节少的转为字节多的高位补0没有异议，但是是强转为字节少的，损失精度，截取 原数的原码（还是补码） 的低位部分 是作为 新数的原码（还是补码） 各有说法。通过4个例子验证一下。验证结果是：将原数的补码 的低位部分 作为 新数的补码。

---

 

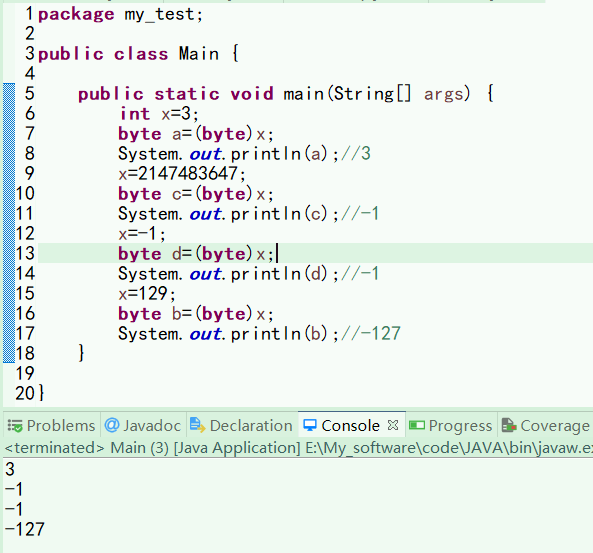
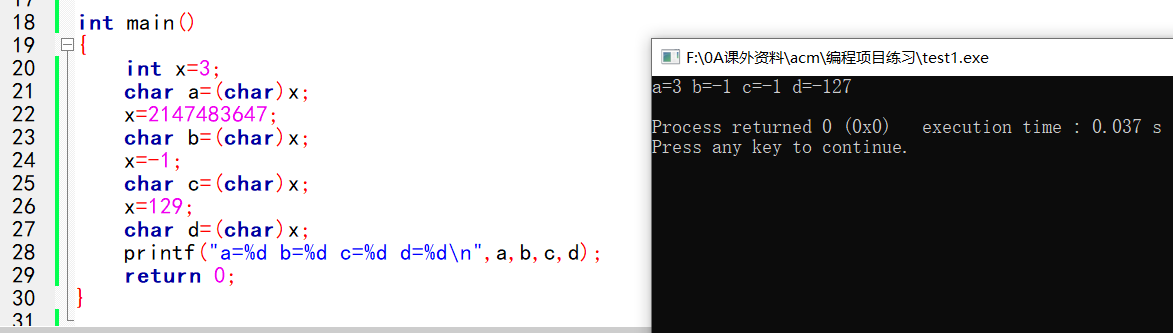
        int x=3;
        byte a=(byte)x;
        System.out.println(a);//3

3的二进制各种码都一样，为00000000 00000000 00000000 00000101；截取低位8位，00000101，无论怎么表示都是正数，说法x的原码截取后8位给a当原码，或者x的补码截取后8位给a当补码都说得通。甚至说x的补码截取后8位给a当原码都是对的。

        x=2147483647;
        byte c=(byte)x;
        System.out.println(c);//-1

2147483647的二进制各种码都一样，为11111111 11111111 11111111 11111111；截取低位8位，11111111，当作-1的补码；

        x=-1;
        byte d=(byte)x;
        System.out.println(d);//-1

-1的二进制原码是10000000 00000000 00000000 00000001，反码是11111111 11111111 11111111 11111110，补码是11111111 11111111 11111111 11111111；-1的byte型补码也是11111111，显然是x的补码截取后8位给d当补码。如果是原码截取作为原码则输出应该是1，显然不可能是原码的截取。真相已经呼之欲出了，再测一个129。

        x=129;
        byte b=(byte)x;
        System.out.println(b);//-127

129的二进制各种码都一样，为00000000 00000000 00000000 10000001；-127的byte型补码是10000001，据此推测强转损失精度的取值方法是截取原数的二进制补码低位部分作为新数的二进制补码。对应了开篇第一句话：在计算机中，数据一律是用二进制补码来存储。

 

 

补充

1.两数相加，若最高位(符号位)有进位，则进位被舍弃。

 

 

2.减法运算也可以当作加法运算