matlab-线性回归

1.调用函数regress(Y,X,alpha)，plpha是置信度，如果直接用regress(Y,X)则默认置信度为0.05，Y是一个 的列向量，X是一个 的矩阵，其中第一列是全1向量。

 

2.函数返回值及意义

b 回归系数，是一个一维向量，第一个是回归方程的常数b₀

bint 回归系数的置信区间，是一个2列的矩阵

r 残差

rint 残差置信区间，是一个2列的矩阵

stats 用于检验回归模型的统计量，有4个统计量，按输出顺序分别是相关系数R²，F值，与F对应的概率p，误差方差。

相关系数R²越接近1，说明回归方程越显著；F > F1-α（k，n-k-1）时拒绝H₀，F越大，说明回归方程越显著；与F对应的概率p 时拒绝H₀，回归模型成立。p值在0.01-0.05之间，越小越好。

 

3.出残差及其置信区间rcoplot(r,rint);结果是一个图

 

4.一元线性回归，y=b₀ + b_{1 *} x；

定义两个长度相同的一维数组后调用函数。

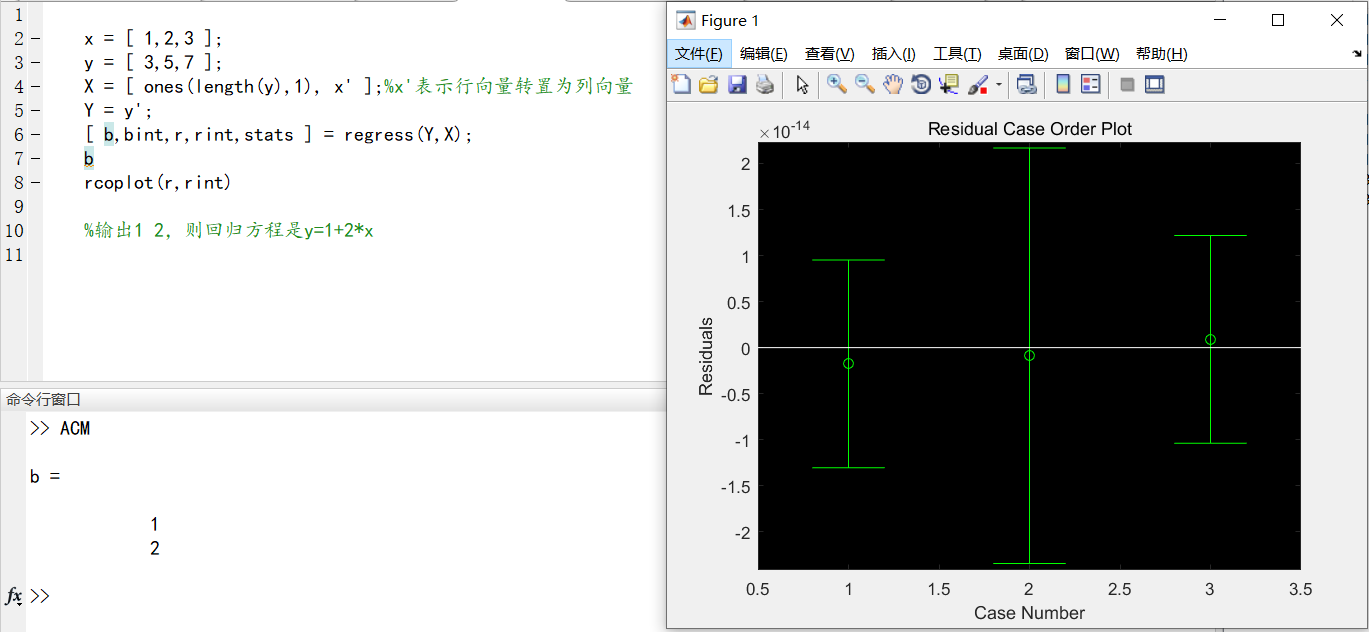
x = [ 1,2,3 ];
y = [ 3,5,7 ];
X = [ ones(length(y),1), x' ];%x'表示行向量转置为列向量
Y = y';
[ b,bint,r,rint,stats ] = regress(Y,X);
b
rcoplot(r,rint)
%输出1 2，则回归方程是y=1+2*x

 

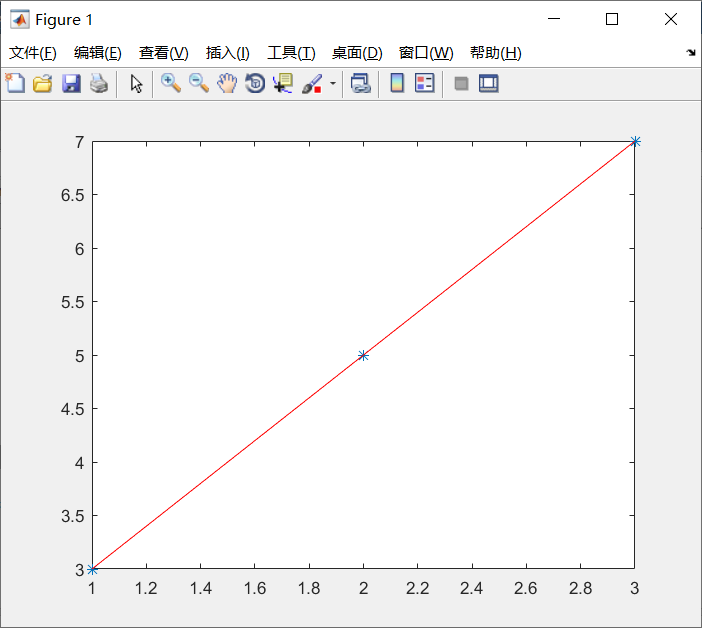
绘制图表：plot(x,Y,'*',x,z,'r');%'*'表示原来的各个点，'r'表示回归方程连起来的线

 

 

 

5.多元线性回归，照着上面模板套用即可

y=[1 2 3 4 5 6 7 8];
%f是一个10*8的矩阵
x1=f(1,:);
x2=f(2,:);
x3=f(3,:);
x4=f(4,:);
x5=f(5,:);
x6=f(6,:);
x7=f(7,:);
x8=f(8,:);
x9=f(9,:);
x10=f(10,:);%把f的每一行赋值给各个xi
X=[ ones( length(y),1 ), x1',x2',x3',x4',x5',x6',x7',x8',x9',x10'];%把行向量转为列向量
Y=y';
[ b,bint,r,rint,stats ] = regress(Y,X);

　　

 

 

 

参考：https://blog.csdn.net/u011089523/article/details/79203375