hdu5698瞬间移动-（杨辉三角+组合数+乘法逆元）

瞬间移动

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2404    Accepted Submission(s): 1066

Problem Description

有一个无限大的矩形，初始时你在左上角（即第一行第一列），每次你都可以选择一个右下方格子，并瞬移过去（如从下图中的红色格子能直接瞬移到蓝色格子），求到第n 行第m 列的格子有几种方案，答案对1000000007 取模。

 

 

Input

多组测试数据。

两个整数n,m(2≤n,m≤100000)

 

 

Output

一个整数表示答案

 

 

Sample Input

4 5

 

 

Sample Output

10

 

 

解题过程：

先看一下杨辉三角的图：

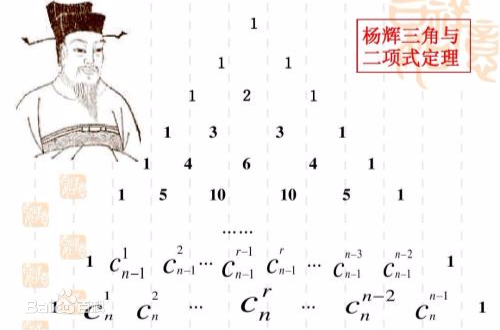
矩阵从a【1】【1】开始，先枚举题目的少数答案：

0  0  0  0  0  0  0
0  1  1  1  1  1  1
0  1  2  3  4  5  6
0  1  3  6  10 15 21
0  1  4  10 20 35 56
0  1  5  15 35 70 126
0  1  6  21 56 126 252 显然斜着看是一个杨辉三角。

 

从左上到右下看作一行一行，从左下到右上数该行第几个。
C（x,y） 斜着看，第x行y个
杨辉三角有效部分可用组合数表示为
(0,0) (1,1) (2,2) (3,3) (4,4) (5,5)
(1,0) (2,1) (3,2) (4,3) (5,4)
(2,0) (3,1) (4,2) (5,3)
(3,0) (4,1) (5,2)
(4,0) (5,1)
(5,0)

 

输入n，m表示n行m列。对应到组合数里。选择杨辉三角部分。
a[n][m]
(2,2) (2,3) (2,4) (2,5) (2,6)
(3,2) (3,3) (3,4) (3,5) (3,6)
(4,2) (4,3) (4,4) (4,5) (4,6)
(5,2) (5,3) (5,4) (5,5) (5,6)
(6,2) (6,3) (6,4) (6,5) (6,6)

 对于从左下到右上这一斜线，n+m相等。

 

将矩形数组a[n][m]和组合数C(x,y)联系起来，我们是利用组合数C(x,y)来算答案,故用x和y表示输入的n和m

对于纵坐标，永远都是y=m-2

对于横坐标，捉摸不定，找出第一列的规律，x=n-2

利用矩阵中n+m相等的条件，推出C(x,y)=C(n+m-4,m-2)。

 

由于n和m巨大，并且题目中的模数p为素数。

求组合数，C(n,m)%p = n! / ( m!*(n-m)! ) %p

用乘法逆元配合快速幂可以解决，本题还不需要用到卢卡斯定理。

 

 AC代码：

 

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
const ll p=1e9+7;

ll fact[1000005];

void init()
{
    memset(fact,0,sizeof(fact));
    fact[0]=fact[1]=1;
    for(ll i=2;i<1000005;i++)
        fact[i]=fact[i-1]*i%p;

}

ll power(ll a,ll b,ll p)
{
    ll res=1;
    while(b)
    {
        if(b%2)
            res=res*a%p;
        b=b/2;
        a=a*a%p;
    }
    return res%p;
}

ll C(ll n, ll m ,ll p)
{   ///C(n,m) = n! / ( m!*(n-m)! )
    ///数据太大肯定爆，p又是素数。换成求m!*(n-m)!的逆元，又不能一起求，会爆数据，分开求，看做n!/m! * 1/(n-m)!
    ///由于是对p求模，n，m范围在阶乘表范围里
    if(m>n)
        return 0;
    return fact[n] * power(fact[m], p-2, p)%p * power(fact[n-m], p-2, p) % p;
    ///fact * power * power 可能爆long long，第二次就要取模
}

int main()
{
    init();
    ll n,m;
    while(scanf("%lld%lld",&n,&m)!=EOF)
    {
        ll ans=C(n+m-4,m-2,p);
        printf("%lld\n",ans);
    }
    return 0;
}