Image Restoration[Deep Image Prior]
0.背景
这篇论文是2017年11月29号第一次提交到arxiv并紧接着30号就提交了V2版本的。
近些年DCNN模型在图像生成和修复上面表现很好,大部分人认为好的原因主要是由于网络基于大量的图片训练,从数据中获取了足够的信息,从而使得模型性能这么好。然而Dmitry Ulyanov等人的这篇论文让我们看到了不一样的解释,他们通过实验发现:
- 人为设计的网络结构(主要还是cnn,毕竟这里讨论的是图像)本身就能够抓取大量低层级的图像统计先验信息,也就是说网络结构本身就差不多等于传统的如hog等这样人为设计的特征提取方式。
当然作者也从《Understanding deep learning requires rethinking generalization》中得到灵感,在该论文中C. Zhang等人用在一个训练集上表现很好的网络结构去基于另一个label都是随机给定的数据集上进行训练,发现居然出现了过拟合的现象。所以不能简单的将模型的性能归功于大量图像数据本身的信息。Dmitry Ulyanov等人认为,还有网络结构本身的作用没有分析清楚。
Dmitry Ulyanov等人使用未被训练的cnn网络(其中的权重都是随机初始化的),然后数据上只需要输入一张被损坏的图片。在这个过程中,网络的权重扮演着图像恢复时候所需要的参数:即给定一个随机初始化的网络,然后基于给定的受损图片和任务依赖的观测模型,通过迭代使得模型参数逼近最大似然。
该方法在标准的图像处理问题比如消噪、修补、超分辨率上表现都很不错。当然作者也通过一个应用来分析dnn中激活值所包含的信息。而且就如TV范式一样,不通过学习,而是通过类似手动设计的方式表示的正则化,使得生成的结果避免了如学到的正则化导致的潜在bias问题(bias,variance是2个用来评价模型好坏的策略)。
1.Deep Image Prior
DNN用来做图像生成的原理就如自动编码器的解码部分一样,即学习一个生成器(也可以如AE中叫做解码器)。该方法可以从随机分布中采样真实的图片,甚至这个分布还能限制成如受损的观测样本\(x_0\)表示的分布。这样的想法自然可以应用于解决逆向的问题,如消噪和超分辨率。作者主要研究了在基于未训练的基础上,不同的生成器网络结构隐式抓取的先验。所以网络本身就可以解释为如下参数化的形式:
其中\(x\in R^{3\times H \times W}\),\(z\in R^{C' \times H' \times W'}\),\(z\)就是一个编码的张量(或者向量),\(\theta\)就是网络的参数。该网络结构是交替的使用如卷积、上采样、非线性激活函数等操作。具体的,作者大部分的实验都是使用如AE一样的“沙漏”结构,并且使用多达2百万的参数量。
ps:说白了,就是
- 1 - 设计一个如下面图1.2.1的类AE的CNN网络结构,其中权重是随机初始化的;
- 2 - 输入是一个和输出一样大小的图片(像素值是随机产生的);
- 3 - 目标函数就是如AE一样,力求输出的和目标相似,\(\min||x-x_0||\),在这其中\(x\)是网络输出的,\(x_0\)是给定的需要恢复的图片,如需要去噪的图片;
- 4 - 如往常的模型一样采用如Adam方法训练,待稳定,或者自己随便设定迭代次数;
- 5 - 此时照样输入第二步那张随机产生的图片,经过网络,得到输出。该输出就是去噪了的图片。
1.1 原理描述
消噪、超分辨率、修复等任务都可以表示成一个能量最小化的问题:
其中\(E(x;x_0)\)是一个任务依赖的数据项,\(x_0\)是一个噪音的(低分辨率、被遮挡)图片,\(R(x)\)是一个正则化项。
因为\(E(x;x_0)\)是基于具体的任务而选择的,所以这里先介绍下第二项,也就是一个抓取自然图片上通用先验的正则化项,它相比第一项更困难,而且是许多研究论文的重点。
举个简单的例子,\(R(x)\)可以是一个图像的Total Variation(TV),从而希望训练好的模型能够包含统一区域。
而在这里,作者很机制的将\(R(x)\)用一个神经网络(用它来抓取隐式先验)来代替,其中网络的参数选取如下:
其中,最小的参数\(\theta^*\)是通过基于一个随机初始化网络基础上,采用Adam等方式训练得到的。给定一个(局部)最优的参数\(\theta^*\),图像恢复的过程如\(x^*=f_{\theta^*}(z)\)。这里的编码\(z\)也是可以优化的,不过作者这里只进行了随机初始化,并且保持固定不变
通过公式1.1.2定义的公式1.1.1中的先验\(R(x)\)是一个指示函数:
- \(R(x)=0\):当图像可以基于一个具体的CNN结构从\(z\)中推测得出;
- $R(x)=+\infty $:其他信号
因为该网络结构没有经过预训练和其它方式,所以这样一个deep image prior是完全人为设计的,就如TV norm一样。作者通过实验发现,这样的手动设计的先验对于各种不同的图像恢复任务来说效果还是很好的。
1.2 模型结构
作者发现设计的网络结构中如果short paths(ResNet中的快捷连接)不是很多的话,还是能够表示一个很好的deep proirs;而如果short paths太多的话,就会阻止网络学习其中规律的图像模式,导致生成的是像素级别的记忆和不够充分的image prior。Dmitry Ulyanov等人主要用全卷积结构来构造网络结构,其中\(z\in R^{C'\times W\times H}\)和网络的输出空间分辨率是一致的,即\(f_\theta(z)\in R^{3\times W\times H}\).大致网络结构如图1.2.1
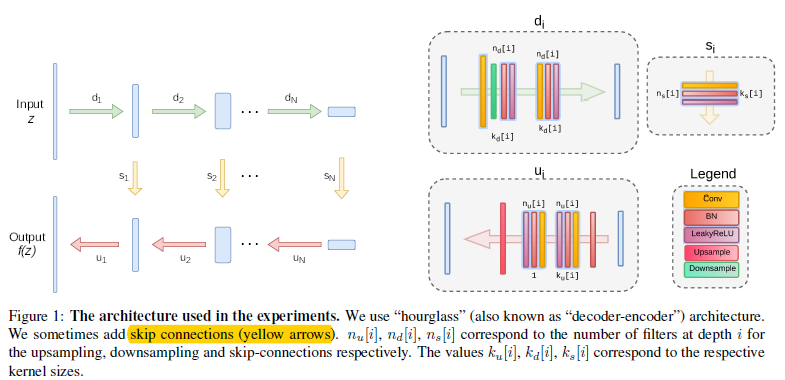
图1.2.1 网络结构示意图
虽然可以通过对每个任务都谨慎的调整结构,甚至对每个图片都调整结构来达到最好的结果。不过作者发现在一个大致的范围内,超参数和结构都得到差不多的结果,作者使用了LeakyReLU来作为激活函数,下采样是基于卷积调整stride来实现的。并且发现基于Lanczos核进行平均和最大池化的下采样没什么差别。对于上采样来说,作者选择双线性上采样和最近邻上采样。另一种上采样的方法是使用转置卷积,不过结果很差;除了特征反转实验外,作者在卷积层中使用反射填充而不是零填充。
对于输入,作者用了两种不同的方式:
- 1 - 随机,即\(z\)用【0,0.1】的均匀分布来填充;
- 2 - 用np.meshgrid来初始化\(z\in R^{2\times W\times H}\)
图1.2.2 第二种初始化\(z\)的方法
这样的初始化方式扮演了一个额外的平滑先验,而且这样的输入对大洞修复任务(遮挡区域是个大洞)还是很有益的。在网络拟合的时候,我们有时候使用的是基于噪音的正则化,即在每次迭代中通过一个额外的标准噪音来扰乱输入\(z\)。虽然作者发现这种正则化阻碍了优化过程,但还观察到,无论加性噪声的方差如何,网络都能够优化其目标为零(即,网络总是能够在迭代足够多的优化步之后去适应任任何合理的方差)。
1.3 高噪音阻抗的参数化
也许有人会疑惑,为什么一个high-capacity的网络\(f_\theta\)可以作为一个先验。事实上,我们只期望能够找到参数\(\theta\)可以去恢复任何包含了随机噪音的图像\(x\),所以该网络在其生成的图片上不应该带入任何的限制才对。不过作者的工作显示,虽然大部分图像的确都可以被拟合,不过网络结构的选择对于解空间的搜索还是一个主要的影响。比如网络比较抵制“坏”的解,并且对于看似自然的图片收敛的更快。
如果将这个影响进行量化,那么引入一个最基本的重构问题:给定一个目标图像\(x_0\),我们希望找到参数集合\(\theta^*\)可以重构这个图像。该问题可以被认为是基于1.1.2基础上,使用如下式子作为数据项:
将上述式子插入到1.1.2中,得到如下优化问题:
首先基于下面这四种情况:

图1.3.1 4种不同的图片输入
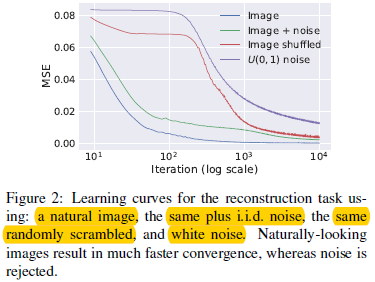
图1.3.2 基于4种不同情况下的能量函数值迭代收敛
可以看出在1和2下,mse下降的最快;而在情况3和4上,参数化还是有着明显的"惯性"。因此,虽然在受限情况下参数化可以拟合无结构的噪音,不过他还是很耐抗的,换句话说,参数化提供了对噪音的高阻抗和信息的低阻抗。
因此上述结论就是,可以限制1.1.2的优化过程中的迭代次数,得到的先验(迭代后的模型)可以将\(z\)通过参数为\(\theta\)的CNN映射到一个图像空间的子集上,并且\(\theta\)和随机初始化的\(\theta_0\)没太大差别。
参考文献:
[] - C. Zhang, S. Bengio, M. Hardt, B. Recht, and O. Vinyals. Understanding deep learning requires rethinking generalization. In Proc. ICLR, 2017
[TV norm] - A. Mahendran and A. Vedaldi. Understanding deep image representations by inverting them. In Proc. CVPR, 2015





