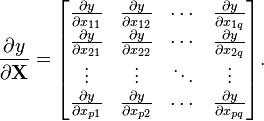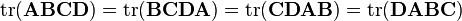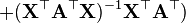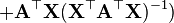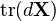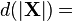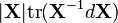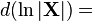数学-矩阵计算(4)两种布局
本博文来自维基上的矩阵计算:https://en.wikipedia.org/wiki/Matrix_calculus#Denominator-layout_notation
之前会发现在有的求导上最后结果需要转置,而有的不需要,很困惑,然后才发现了这个维基上面的解释(这才是写该博文的主要价值,注意到不同的布局问题,其他部分只是为了完整性而写的),而且下面也有很多很不错的参考链接,其中就有之前的矩阵计算(2)和矩阵计算(3)的链接。维基最后更新时间:17 April 2015, at 21:34.
matrix calculus
在数学上, 矩阵微积分是用来表示多变量的微积分,当然主要还是在矩阵空间上的。它覆盖了单一函数(单元)关于多变量的偏导,多变量函数(多元函数)关于单一变量、向量和矩阵的偏导(向量、矩阵可以被视为单一实体对待)。这种符号化的数学表示大大的简化了很多操作,例如查找多变量函数的最大值或者最小值,以及微分方程的求解系统等等。值得注意的是:下面使用的符号是在统计和工程领域中常用的,不过张量的指数表示(tensor index notation)是来自物理学。
不过有个我们之前未注意的是,有两派人它们使用着自己的符号约定,从而将矩阵微积分划分成了两个派别。这两个派别很容易区分,只要看它们写一个标量关于一个向量的导数是写成列向量还是行向量。不过这两个约定都是被大家所接受的,就算是在涉及到一般的矩阵计算的时候,将常规的向量默认视为列向量(而不是行向量)的情况下还是成立的。在矩阵微积分中,如果采取了一个约定,那么就使用该约定贯穿整个领域(例如:计量经济学,统计学,评估理论(etimation theory)和机器学习),不要混用不然会造成混乱。然而,在一个具体的领域中,不同的作者还是会使用不同的约定,因为会有来自不同派别的作者会将他们自己的约定作为标准。所以在没有去仔细的验证不同作者的资料的时候盲目的将他们的结论放在一起会有严重的错误。因而在一个完整的资料上需要确保符号的一致性。在下面的布局约定部分会有两种约定的定义介绍和比较。
一、范围
矩阵微积分指的是使用矩阵和向量来表示因变量每个成分关于自变量每个成分的导数。通常来说,自变量指的是标量、向量或者矩阵,而因变量指的是由自变量得到的结果。每种不同的情况会导致有不同规则集合(或者不同的微积分操作)。我们可以用有组织的矩阵符号来方便的表示不同的导数。
第一个例子,考虑向量微积分中的梯度。对于一个有着三个因变量的标量函数来说, 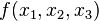 ,可以通过下面的向量方程来表示梯度:
,可以通过下面的向量方程来表示梯度:
这里  表示
表示 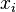 方向上的单元向量,其中
方向上的单元向量,其中  。该导数更广义的表示为:一个标量 f 关于一个向量
。该导数更广义的表示为:一个标量 f 关于一个向量 的导数,其结果的向量形式如下:
的导数,其结果的向量形式如下:
-
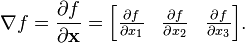 [这不是通常的向量表示形式,通常的向量是表示成列向量]
[这不是通常的向量表示形式,通常的向量是表示成列向量]
更多复杂的例子,例如标量函数关于矩阵的导数,被称之为梯度矩阵,其中每个对应位置上的元素都是关于原始矩阵每个元素的导数。在这种情况下,一个标量(个人:也就是结果矩阵中的一个元素)就是矩阵中每个因变量的一个函数。另一个例子,如果我们有一个元素为因变量、函数、m个自变量的n维向量,我们就需要考虑因变量向量关于该自变量向量的导数。结果为表示所有可能导数组合的一个m×n 矩阵。当然,最多也就9种形式。如果我们在自变量和因变量中有更多层次的嵌套,那么组合数量就远远不止9种了。
下面表中就是以矩阵形式表示的常见的6种不同的导数形式。[1]
| 类型 | 标量 | 向量 | 矩阵 |
|---|---|---|---|
| 标量 | 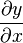 |
 |
 |
| 向量 |  |
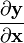 |
|
| 矩阵 | 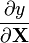 |
因为向量和标量都可以表示成简单的矩阵形式,所以这里我们使用“矩阵”来泛化的表示所有含义。而且,我们使用黑体字母来表示向量,而黑体大写字母表示矩阵。
当然上面的9个格子还少了几个组合,比如向量关于矩阵的导数等。不过,这些导数是以秩(rank)超过2的张量(tensor)表示的,所以它们不适合放在一个矩阵中。接下来的三个部分中,我们会这些导数,而且将他们与其他的数学分支联系起来。在下面的布局约定部分有更详细的表。
1.1 其他导数
矩阵导数这种符号可以很方便的用来表示微积分中的偏导数。Fréchet导数是泛函分析中求关于向量的导数的标准方式。在这种情况中,矩阵的矩阵函数是Fréchet可微分的,这两个派别的导数在符号的解释上是需要保持一致的。正如在一般的偏导数分析中,许多公式是在比现有的近似线性映射的导数下还弱的分析条件下扩展得到的。
1.2 用法
矩阵微积分可以用来计算最优随机估计(optimal stochastic estimators),通常会涉及到 拉格朗日乘子的使用。比如下面的几个例子:
二、符号
该小节的向量和矩阵导数遵循矩阵符号的规则,使用单个变量来表示一个包含着大量变量的实体。在该规则中,我们需要通过字体来区分标量,向量和矩阵。M(n,m)表示n行m列的实数矩阵空间。这样的矩阵以黑体大写字母表示:A, X, Y, etc.M(n,1)也就是一个列向量,表示成黑体小写字母:a, x, y, etc.M(1,1)也就是一个标量,表示成小写斜体字母:a, t, x, etc. XT 表示矩阵的转置, tr(X)表示迹,而det(X)表示的是行列式。所有的函数都假设是可微分类别 C1 的,除非有特别说明。字母表中上半部的普通的字母(a, b, c, …)用来表示常量,下半部字母(t, x, y, …)用来表示变量.
NOTE: 正如最开始说的,在向量和矩阵中关于偏导数的表示是不唯一的,因为没有一个完整的标准。下面两个介绍性的部分使用分子布局约定来简单的说下符号带来的便利,主要是为了避免过多的复杂讨论。在后面的布局约定中有更详细的介绍。我们应该注意到:
- 先不说"分子布局" 和"分母布局",其实还有其他的符号化解释。选择这两种的原因(或者在某些情况下,叫做分子布局,混合布局),是因为这样可以独立的解释标量关于向量, 向量关于标量,向量关于向量,和标量关于矩阵的导数,当然,有很多作者会以各种不同的方式来混用这些布局。
- 下面的介绍性部分使用分子布局,不代表这是“正确的”或者“优先”的选择。不同的布局类型都有优点和缺点。粗心的将不同的局部混合使用会导致很严重的错误,而且从一个布局转移到另一个布局也是需要谨慎对待的。所以,当在当前使用的公式中,最好的选择就是先验证使用的是什么布局,然后考虑遵循这个布局,不要试图在所有的情况下使用同一个布局(个人:就是如果你在推导一个公式,先了解该作者用的是什么布局,而不要以为所有的资料都是同一个布局。当然最好对每个公式都先验证下,这是为了防止有些作者在同一份资料中混乱的使用不同的布局)。
2.1 其他选择
使用爱因斯坦求和约定的张量指数表示(tensor index notation)非常像矩阵微积分,只是它是一次只有一个成分。它可以很轻松的对任意高秩的张量进行操作,因为秩超过2的张量不能够很好的通过矩阵符号来处理。这里所有的工作都可以以这种不使用单一变量的矩阵符号来完成。不过,在评估论和应用数学领域上,是需要对超多指数(indices)进行操作的,在这些领域中,矩阵微积分是很常见的。同样的,爱因斯坦符号可以作为通常的元素符号的替代方法,来表示这里的identities,不过当需要显式的求和的时候,这就变得很麻烦了。其实一个矩阵可以认为是有着秩为2的张量。(个人:该段的意思就是除了前两种表示法还有个张量指数表示法,具体的这里不介绍,可以看下面的参考文献。)
三、有关向量的导数
因为向量就是有着一列的矩阵。最简单的矩阵导数就是向量导数。
这里的符号可以用来表示一般的向量微积分操作,用欧式空间Rn中n维向量表示M(n,1),而实数空间R 实数表示M(1,1)。
NOTE:这里使用分子布局只是为了教学。有些作者还是会使用不同的约定的。下面的布局约定部分会有更详细的解释.
3.1 向量关于标量
在向量微积中,向量y 关于标量x 的导数被称为向量y
的目标向量,  。 注意:y:R
。 注意:y:R  Rm.
Rm.
Example;例如在欧式空间中,速率向量就是位置向量的目标向量(即关系到时间的函数)。同样,加速度也是速率的目标向量。
3.2 标量关于向量
标量y 关于向量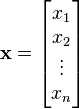 的导数的结果如下:(以分子布局约定)
的导数的结果如下:(以分子布局约定)
空间向量 x 的标量函数f(x)在单位向量 u上的方向导数定义成的梯度形式如下:
之前,标量关于向量的导数的符号可以重写成方向导数的形式: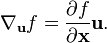 这种符号表示形式在乘积规则和链式规则的时候可以看起来和标量导数一样可读.
这种符号表示形式在乘积规则和链式规则的时候可以看起来和标量导数一样可读.
3.3 向量关于向量
之前的两种情况可以被认为是向量关于向量的导数的应用,只是其中某个向量的大小为1罢了。同样的,我们可以以同样的方式从向量推广到矩阵上。
向量函数(一个向量,其中的元素都是函数)  关于一个输入向量
关于一个输入向量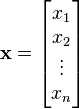 的导数可以写成如下形式:(分子布局约定)
的导数可以写成如下形式:(分子布局约定)
在向量微积分中,一个向量函数y 关于一个向量x(其成分被称之为一个空间)的导数被称之为pushforward或者differential, 或者是Jacobian矩阵.
在 Rm 中,pushforward即为向量函数f 关于向量v 的导数为:
四、关于矩阵的导数
有两种关于矩阵的导数类型,它们可以表示成大小相同的矩阵形式。即矩阵关于变量的导数和变量关于矩阵的导数。这在应用数学的许多领域中为了找到最小值问题是很有帮助的,它们可以被称之为:目标矩阵和梯度矩阵。
NOTE: 该部分使用分子布局约定也是出于教学目的。
4.1 矩阵关于标量
矩阵函数 Y 关于标量x 的导数被称之为 目标矩阵: (以分子布局约定)
4.2 标量关于矩阵
自变量为矩阵X 的标量函数 y 关于矩阵X的导数为:(分子布局约定)
注意到这里关于X的梯度的索引就是矩阵X索引的转置。(矩阵的标量函数会涉及到矩阵的迹和行列式)。
该导数也可以写成如下形式:
同样,矩阵 X 的标量函数f(X)在矩阵 Y的方向上的方向导数为:
这就是梯度矩阵,常用来解决评估论中的最小化问题,特别是在卡尔曼滤波的导数中占据着重要的地位。
4.3 其他矩阵导数(这部分的内容是有争议的,09年7月)
之前没写的三个导数就是向量关于矩阵的,矩阵关于向量的,矩阵关于矩阵的。这几个因为不同派别观点不同,而且没有个统一的符号表示。对于向量来说,前面的两个可以看成是矩阵关于矩阵的导数,只是对应的矩阵是一行或者只有一列。所以,这一小节我们就只介绍矩阵关于矩阵的导数。
假设有将 n×m 的矩阵映射到p×q 的矩阵上的函数, F : M(n,m)  M(p,q)。微分或者说矩阵函数 F(X)
关于矩阵的导数是M(p,q) ? M(m,n)的元素, 而且是一个4秩张量(m 和 n 的转换,表示是M(n,m)的对偶空间).简单来说,就是一个m×n 矩阵,其中的每个元素都是一个p×q 矩阵.
M(p,q)。微分或者说矩阵函数 F(X)
关于矩阵的导数是M(p,q) ? M(m,n)的元素, 而且是一个4秩张量(m 和 n 的转换,表示是M(n,m)的对偶空间).简单来说,就是一个m×n 矩阵,其中的每个元素都是一个p×q 矩阵.
其中每个  是一个p×q 矩阵。注意:这个矩阵的索引是转置了的:m 行n 列。在M(n,m)空间中,自变量为n×m 矩阵Y的
函数F 的pushforward为:
是一个p×q 矩阵。注意:这个矩阵的索引是转置了的:m 行n 列。在M(n,m)空间中,自变量为n×m 矩阵Y的
函数F 的pushforward为:
-
 分块矩阵形式
分块矩阵形式
该定义是个通用形式,其他上述的定义都可以作为该定义的特例。
依据 Jan R. Magnus 和Heinz Neudecker的理论,下面的符号都不合适,如果使用这些符号的话,第二个生成的矩阵的行列式将会“无法解释”和“不存在可以使用的链式规则”:[2]
- 给定
 ,
一个自变量为
,
一个自变量为  的矩阵
的矩阵  的可微分函数的导数为:
的可微分函数的导数为:
-
- 给定
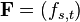 ,一个自变量为
,一个自变量为 的矩阵
的矩阵 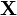 的可微分
的可微分 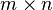 大小的函数的导数:
大小的函数的导数:
-
根据Magnus and Neudecker,[2],Jacobian矩阵为
五、布局约定
该部分讨论在使用矩阵微积分的各种不同领域中使用的符号化约定的相似和不同。当然目前有两大阵营,不过很多作者发现在很多时候将这两种约定混合起来使用会很方便。
最基本的问题就是向量关于向量的导数:即 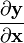 。不过这通常会写成2种不同的形式。如果分子y 是m维的,而分母x 是n维的,那么结果可以是一个m×n 矩阵或者是一个n×m 矩阵,即 y 的元素是列排序,而 x 的元素是行排序,或者说相反。这使得会有以下几种情况:
。不过这通常会写成2种不同的形式。如果分子y 是m维的,而分母x 是n维的,那么结果可以是一个m×n 矩阵或者是一个n×m 矩阵,即 y 的元素是列排序,而 x 的元素是行排序,或者说相反。这使得会有以下几种情况:
- 分子布局,即按照 y 和xT (相比较于x)的布局。这有时候被称为Jacobian 形式.
- 分母布局, 即按照 yT 和 x (相比较于y).这有时候被称之为Hessian 形式.许多作者称这种布局为梯度,区别于 Jacobian (分子布局),是它的转置。 (不过,"梯度"更多的是用来表示导数
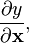 而不是指布局)
而不是指布局) - 第三个可能的形式是将导数写成
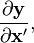 (即导数是关于x的转置的),却遵循分子布局。这使得我们可以认为说矩阵是按照分子和分母制定的。不过在实际中,这生成的结果是和分子布局一样的。
(即导数是关于x的转置的),却遵循分子布局。这使得我们可以认为说矩阵是按照分子和分母制定的。不过在实际中,这生成的结果是和分子布局一样的。
当处理梯度  和想法的情况
和想法的情况  (逗号消不掉)的时候,我们有着相同的问题。为了保证一致性,我们应该采用下面的某一条方案:
(逗号消不掉)的时候,我们有着相同的问题。为了保证一致性,我们应该采用下面的某一条方案:
- 如果我们对
 (逗号消不掉)选择分子布局,我们应该将梯度
(逗号消不掉)选择分子布局,我们应该将梯度  写成行向量,
写成行向量,  为列向量。
为列向量。 - 如果我们对
 (逗号消不掉)选择分母布局,我们应该将梯度
(逗号消不掉)选择分母布局,我们应该将梯度 写成列向量,
写成列向量, 写成行向量。
写成行向量。 - 第三种情况,我们采用
 和
和  然后使用分子布局。
然后使用分子布局。
不是所有的数学教科书和论文都会在整个部分都保持一致性的。也就是有时候在相同的论文的不同部分会使用不同的约定。例如,有些地方选择了分母布局来表示梯度(将它们以列向量表示),而对于向量关于向量的导数 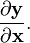 却使用分子布局。
却使用分子布局。
同样的,当面对标量关于矩阵的导数 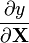 和矩阵关于标量的导数
和矩阵关于标量的导数 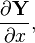 的时候,按照Y和 XT,使用的是分子布局,而按照 YT 和 X使用的是分母布局。然而,在实际中,对
的时候,按照Y和 XT,使用的是分子布局,而按照 YT 和 X使用的是分母布局。然而,在实际中,对 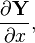 使用一个分母布局,然后按照 YT 来对结果进行布局是很罕见的,因为这样的结果看起来很糟糕,而且不对应标量公式。
所以,我们通常看到的是下面的布局:
使用一个分母布局,然后按照 YT 来对结果进行布局是很罕见的,因为这样的结果看起来很糟糕,而且不对应标量公式。
所以,我们通常看到的是下面的布局:
- 只有分子布局,根据
Y 来写
 ,根据XT来写
,根据XT来写 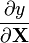 。
。 - 混合布局, 根据Y 来写
 ,根据X来写
,根据X来写 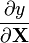 .
. - 使用符号
 结果和分子布局一样。
结果和分子布局一样。
在下面的式子中,我们处理5种可能的组合形式:  和
和  。
我们同样会处理标量关于标量导数的情况,不过这会涉及到一个中间的向量或矩阵。(这是很可能会出现的,例如,一个多维参数化曲线是以一个标量变量定义的,那么在求该曲线的标量函数功能与参数化该曲线的标量的导数的时候,在中间过程中会有向量或矩阵需要计算。)
对于每个不同的组合,我们都给出了分子布局和分母布局,除了那种分母布局很罕见的情况。在那种有意涉及到矩阵的情况下,我们会给出分子布局和混合布局。正如上面说的,向量和矩阵分母写成转置符号的情况等同于分母没有写成转置符号的分子布局。
。
我们同样会处理标量关于标量导数的情况,不过这会涉及到一个中间的向量或矩阵。(这是很可能会出现的,例如,一个多维参数化曲线是以一个标量变量定义的,那么在求该曲线的标量函数功能与参数化该曲线的标量的导数的时候,在中间过程中会有向量或矩阵需要计算。)
对于每个不同的组合,我们都给出了分子布局和分母布局,除了那种分母布局很罕见的情况。在那种有意涉及到矩阵的情况下,我们会给出分子布局和混合布局。正如上面说的,向量和矩阵分母写成转置符号的情况等同于分母没有写成转置符号的分子布局。
还记得之前提醒的,许多作者会混合的使用不同的分子和分母布局表示不同的导数类型,而且没法保证说一个作者会在所有类型上一直使用分子布局或者分母布局。可以通过下面的表来决定对某个具体的导数类型使用什么样的布局,不过注意不要假设其他类型也需要遵循同一种布局。
在计算一个集合(向量或矩阵)分母的导数从而能够找到该集合的最大或最小值的时候,应该记住,使用分子布局生成的结果是关于集合的转置。例如,通过使用矩阵微积分来找到多元正态分布的最大似然估计。如果定义域是一个kx1 列向量,那么使用分子布局的结果是1xk 行向量的形式。所以,使用结果的转置或者使用分母布局(或者混合布局)。
-
集合关于集合的导数结果 Scalar y Vector y (size m) Matrix Y (size m×n) Notation Type Notation Type Notation Type 标量 x 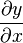
标量 
(分子布局) size-m 列向量
(分母布局) size-m 行向量

(分子布局) m×n 矩阵 向量 x ( n) 
(分子布局) size-n 行向量
(分母布局) size-n 列向量
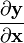
(分子布局) m×n 矩阵
(分母布局) n×m 矩阵

? 矩阵 X (p×q) 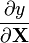
(分子布局) q×p 矩阵
(分母布局) p×q 矩阵

? 
?
分子布局和分母布局的操作结果可以通过转置来切换。
5.1 分子布局符号
使用分子布局:[1]
下面的定义只提供了分子布局的结果:
5.2 分母布局符号
使用分母布局:[3]
六、Identities
正如上面说的,通常来说,操作的结果需要通过转置在分子布局和分母布局之间相互切换。
为了帮助理解下面的所有identities, 记得最重要的规则是:链式规则, 乘积规则和求和规则。 求和规则是普遍适用的,而乘积规则应用在下面的大部分情况中, 其中矩阵乘积的顺序是有要求的,因为矩阵乘积是不可交换的。链式规则应用在下面的某些情况中,不过可惜的是没有应用在矩阵关于标量的导数和标量关于矩阵的导数中(在后者的情况下,大多数情况都是通过在矩阵上迹操作来完成的). 在后者情况中,乘积规则没法直接使用,不过可以通过使用微分identities来等效的完成。
6.1 向量关于向量的 identities
最开始介绍这个是因为所有的向量关于向量的微分可以直接用在向量关于标量或者标量关于向量的微分上,只要将分母或分子的向量变成标量就行。
-
Identities: 向量关于向量 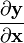
条件 表达式 分子布局,即 y 和 xT 分母布局,即yT 和 x a 不是关于x的函数 
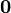
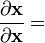

A 不是关于x的函数 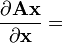
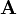

A 不是关于x的函数 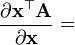

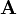
a 不是关于x的函数
u = u(x)

a = a(x), u = u(x) 
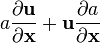

A 不是关于x 的函数
u = u(x)
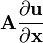

u = u(x), v = v(x) 

u = u(x) 


u = u(x) 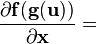

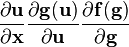
6.2 标量关于向量的 identities[edit]
主要的identities 下面都有条细黑线。
-
Identities: 标量关于向量 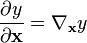
条件 表达式 分子布局,即 xT; 结果是行向量 分母布局,即 x;结果是列向量 a 不是关于x的函数 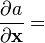
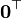 [4]
[4]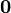 [4]
[4]a 不是关于x的函数,
u = u(x)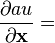

u = u(x), v = v(x) 

u = u(x), v = v(x) 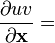
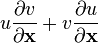
u = u(x) 

u = u(x) 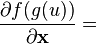

u = u(x), v = v(x) 
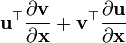
- 假设分子布局 of

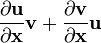
- 假设分母布局 of

u = u(x), v = v(x),
A 不是关于x的函数

- 假设分子布局 of


- 假设分母布局 of

a 不是关于x的函数 
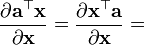
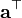
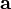
A 不是关于x的函数
b 不是关于x的函数

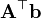
A 不是关于x的函数 


A 不是关于x的函数
A 是对称的


A 不是关于x的函数 

A 不是关于x的函数
A 是对称的
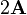



a 不是关于x的函数,
u = u(x)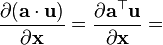
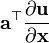
- 假设分子布局of


- 假设分母布局 of

a, b 不是关于x的函数 

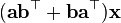
A, b, C, D, e 不是关于x的函数 

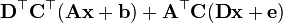
a 不是关于x的函数 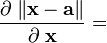

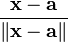
- 假设分子布局 of
6.3 向量关于标量的 identities[edit]
-
Identities: 向量关于标量 
条件 表达式 分子布局,即 y,结果是列向量 分母布局,即 yT,结果是行向量 a不是关于 x的函数 
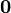 [4]
[4]a不是关于 x的函数,
u = u(x)
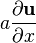
A 不是关于 x的函数
u = u(x)
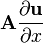

u = u(x) 

u = u(x), v = v(x) 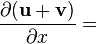
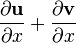
u = u(x), v = v(x) 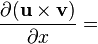
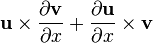
u = u(x) 
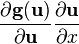

假设矩阵布局是一致的; see below. u = u(x) 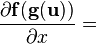
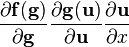
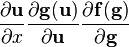
假设矩阵布局是一致的; see below.
NOTE: 设计到向量关于向量的导数的公式 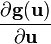 和
和 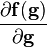 (输出为矩阵)假设矩阵是使用相同的向量布局的,即当使用分子布局向量的时候,就是分子布局矩阵,反之亦然;不过需要转置向量关于向量的导数。
(输出为矩阵)假设矩阵是使用相同的向量布局的,即当使用分子布局向量的时候,就是分子布局矩阵,反之亦然;不过需要转置向量关于向量的导数。
6.4 标量关于矩阵的 identities
注意,当使用矩阵(自变量)的矩阵值(因变量)函数的时候,标量乘积规则和链式规则不存在完全相等的。不过,这类乘积规则也适用于微分形式(见下面),这是得到许多涉及迹函数identites的方法,而且事实上迹允许转置和循环置换,即:
例如,为了计算 
所以,
(最后一步,见 `从微分的导数形式的转换' 部分.)
-
Identities: 标量关于矩阵 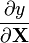
条件 表达式 分子布局,即 XT 分母布局,即 X a 不是 X的函数 
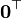 [5]
[5]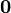 [5]
[5]a 不是 X的函数, u = u(X) 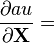
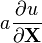
u = u(X), v = v(X) 

u = u(X), v = v(X) 

u = u(X) 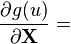

u = u(X) 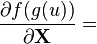

U = U(X) [6] 

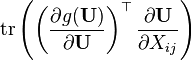
两种形式都假设分子布局for 
如果X 使用分母布局,那么使用混合布局
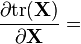

U = U(X), V = V(X) 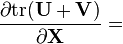
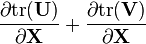
a 不是 X的函数,
U = U(X)
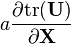
g(X) 是标量系数多项式,或者是无限多项式定义的矩阵函数 (如 eX, sin(X), cos(X), ln(X), 用泰勒展开式); g(x) 是标量函数, g′(x) 是其导数, g′(X) 是对应的矩阵函数 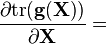

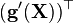
A 不是X的函数 [7] 
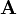

A不是X的函数 [6] 

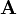
A 不是X的函数 [6] 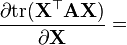
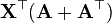
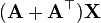
A 不是X的函数 [6] 
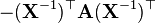

A, B 不是X的函数 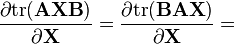


A, B, C 不是X的函数 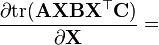

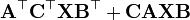
n 是正整数 [6] 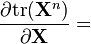
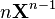

A 不是X的函数,
n 是正整数[6] 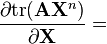
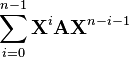
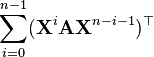
[6] 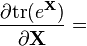
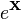

[6] 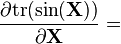


[8] 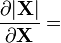
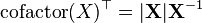

a 不是X的函数 [6] 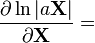 [9]
[9]
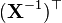
A, B 不是X的函数 [6] 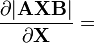
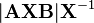

n 是正整数 [6] 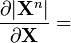

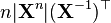
(见 伪逆) [6] 

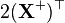
(见 伪逆) [6] 


A 不是X的函数,
X 是方阵而且可逆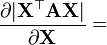
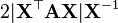
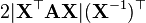
A 不是X的函数,
X 不是方阵,
A 是对称的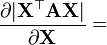

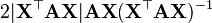
A 不是X的函数
X 不是方阵
A 不是对称的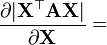


-
6.5 矩阵关于标量的 identities[edit]
-
Identities: 矩阵关于标量 
条件 表达式 分子布局,即 Y U = U(x) 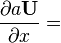

A, B 不是关于x 的函数
U = U(x)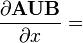
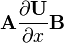
U = U(x), V = V(x) 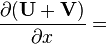
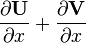
U = U(x), V = V(x) 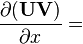

U = U(x), V = V(x) 
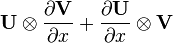
U = U(x), V = V(x) 

U = U(x) 

U = U(x,y) 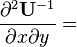

A 不是关于x 的函数, g(X) 是关于标量系数的多项式,或者是关于无限多项式定义的矩阵函数 (如. eX, sin(X), cos(X), ln(X) ); g(x) 是等效的标量函数, g′(x) 是其导数,g′(X) 是对应矩阵函数 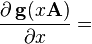
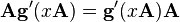
A 不是关于x 的函数 

更多细节可见指数映射的导数。
6.6 标量关于标量的 identities
6.6.1 涉及到向量
-
Identities: 标量关于标量, 涉及到向量 条件 表达式 任意布局 (假定点积忽略行或列布局) u = u(x) 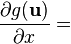

u = u(x), v = v(x) 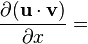
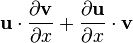
6.6.2 涉及到矩阵
-
Identities: 标量关于标量, 涉及到矩阵[6] 条件 表达式 一致的分子布局,即 Y 和 XT 混合布局,即 Y 和 X U = U(x) 
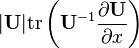
U = U(x) 

U = U(x) 
![|\mathbf{U}|\left[{\rm tr}\left(\mathbf{U}^{-1}\frac{\partial^2 \mathbf{U}}{\partial x^2}\right) + \left({\rm tr}\left(\mathbf{U}^{-1}\frac{\partial \mathbf{U}}{\partial x}\right)\right)^2-{\rm tr}\left(\left(\mathbf{U}^{-1}\frac{\partial \mathbf{U}}{\partial x}\right)\left(\mathbf{U}^{-1}\frac{\partial \mathbf{U}}{\partial x}\right)\right)\right]](https://upload.wikimedia.org/math/8/f/b/8fb5efb6de1f63e377271b882adf1196.png)
U = U(x) 

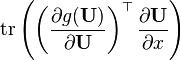
A 不是x 的函数, g(X) 是标量系数的多项式, 或者是由无线多项式定义的矩阵函数(如eX, sin(X), cos(X), ln(X),); g(x) 是等效标量函数, g′(x) 是它导数,g′(X) 是对应矩阵函数 

A 不是x 的函数 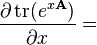
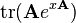
6.7 不同形式中的Identities
通常很容易在微分形式下处理,然后转换成规范导数形式。这只在分子布局下才能很好地work。
-
微分identities: 矩阵[1][6] 条件 表达式 结果(分子布局) A 不是关于 X的函数 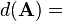

a 不是关于 X的函数 
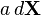



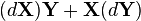
(Kronecker乘积) 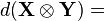

(Hadamard 乘积) 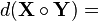
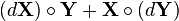


(共轭转置) 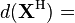
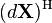
为了转换到标准的导数形式,首先需要转换成以下规范的形式,然后在使用这些identities:
-
从微分的导数形式的转换 [1] 规范的微分形式 等效的导数形式 


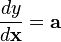
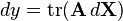
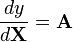
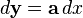

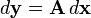


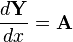
七、See also
八、符号介绍
- Minka, Thomas P. "Old and New Matrix Algebra Useful for Statistics." December 28, 2000. [1]
- ^ Jump up to:a b Magnus, Jan R.; Neudecker, Heinz (1999). Matrix Differential Calculus with Applications in Statistics and Econometrics. Wiley Series in Probability and Statistics (2nd ed.). Wiley. pp. 171–173.
- Jump up^ [2]
- ^ Jump
up to:a b c Here,
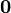 表示一个充满0的n维列向量,这里n是x的长度
表示一个充满0的n维列向量,这里n是x的长度 - ^ Jump
up to:a b Here,
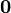 表示一个充满0的矩阵,和X.有着一样的shape。
表示一个充满0的矩阵,和X.有着一样的shape。 - ^ Jump
up to:a b c d e f g h i j k l m n o p Petersen,
Kaare Brandt and Michael Syskind Pedersen. The Matrix Cookbook. November 14, 2008.http://matrixcookbook.com. [3] 该书使用混合布局,即在
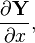 中使用Y,在
中使用Y,在  中使用X。
中使用X。 - Jump up^ Duchi, John C. "Properties of the Trace and Matrix Derivatives" (PDF). University of California at Berkeley. Retrieved 19 July 2011.
- Jump up^ See Determinant#Derivative for the derivation.
- Jump
up^ The constant a disappears in the result. This is intentional. In general,
-
自变量:自变量是指研究者主动操纵,而引起因变量发生变化的因素或条件,因此自变量被看作是因变量的原因。自变量有连续变量和类别变量之分。如果实验者操纵的自变量是连续变量,则实验是函数型实验。如实验者操纵的自变量是类别变量,则实验是因素型的。--来自好搜百科
九、参考资料:
[1] Linear Algebra: Determinants, Inverses, Rank appendix D from Introduction to Finite Element Methods book on University of Colorado at Boulder. Uses theHessian (transpose to Jacobian) definition of vector and matrix derivatives.
[2] Matrix Reference Manual, Mike Brookes, Imperial College London.
[3] The Matrix Cookbook (2006), with a derivatives chapter. Uses the Hessian definition.
[4] The Matrix Cookbook (2012), an updated version of the Matrix Cookbook.
[5] Linear Algebra and its Applications (author information page; see Chapter 9 of book), Peter Lax, Courant Institute.
[6] Matrix Differentiation (and some other stuff), Randal J. Barnes, Department of Civil Engineering, University of Minnesota.
[7] Notes on Matrix Calculus, Paul L. Fackler, North Carolina State University.
[8] Matrix Differential Calculus (slide presentation), Zhang Le, University of Edinburgh.
[9] Introduction to Vector and Matrix Differentiation (notes on matrix differentiation, in the context of Econometrics), Heino Bohn Nielsen.
[10] A note on differentiating matrices (notes on matrix differentiation), Pawel Koval, from Munich Personal RePEc Archive.
[11] Vector/Matrix Calculus More notes on matrix differentiation.
[12] Matrix Identities (notes on matrix differentiation), Sam Roweis.
[13] http://www.psi.toronto.edu/matrix/intro.html#Intro
[14] http://www.psi.toronto.edu/matrix/calculus.html
[15]http://www.stanford.edu/~dattorro/matrixcalc.pdf
[16] http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppD.d/IFEM.AppD.pdf
[17] http://center.uvt.nl/staff/magnus/wip12.pdf
[19] 维基百科https://en.wikipedia.org/wiki/Matrix_calculus#Numerator-layout_notation


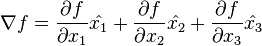
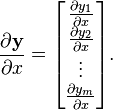
![\frac{\partial y}{\partial \mathbf{x}} =\left[\frac{\partial y}{\partial x_1} \ \ \frac{\partial y}{\partial x_2} \ \ \cdots \ \ \frac{\partial y}{\partial x_n}\right].](https://upload.wikimedia.org/math/7/f/5/7f52f0b5c0cd27fbeaccc76745c1a2a7.png)

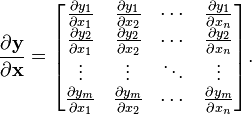
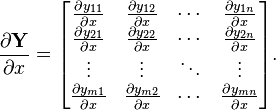
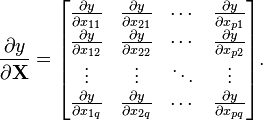


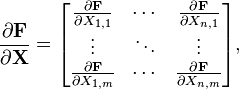
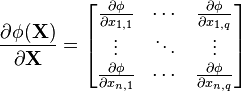
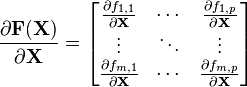
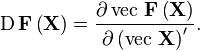
![\frac{\partial y}{\partial \mathbf{x}} =\left[\frac{\partial y}{\partial x_1}\frac{\partial y}{\partial x_2}\cdots\frac{\partial y}{\partial x_n}\right].](https://upload.wikimedia.org/math/0/5/8/058a849a9a78fddbf1e59bcc4fa1f47c.png)
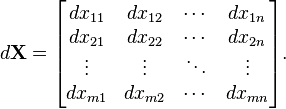
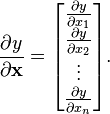
![\frac{\partial \mathbf{y}}{\partial x} = \left[\frac{\partial y_1}{\partial x}\frac{\partial y_2}{\partial x}\cdots\frac{\partial y_m}{\partial x}\right].](https://upload.wikimedia.org/math/b/4/b/b4b563beb83701f5f3854e277f4f4f6e.png)