联邦学习[隐私集合求交PSI]
隐私集合求交,PSI,即private set intersection,
看到一篇讲解psi很细致的文章,想着搭配流程图会更容易理解
0 引言
隐私集合求交,就是在双方不泄露任何额外信息基础上,得到双方的数据交集。也就是双方PSI之后,只知道哪些数据对方也有,除此之外一无所知。对于PSI,我们可以简单想象如下2种实现方式
0.1 纯hash
这种问题大大的有,假设Alice和Bob约定互相基于手机号求交,
1)Alice想发起和Bob的求交,则Alice还得告诉Bob对应的hash函数是啥,
2)然后Alice将自己数据全部hash后,将结果全部传给Bob
3)此处,bob就可以通过穷举方式获得Alice的所有数据了
可以看出谁传hash结果,谁就被动泄露了。
0.2 RSA加密
一图胜过千言,假设Alice发起和Bob的求交,如下图,则Bob可以知道双方的交集是什么,可以直接回传这部分数据,或者反过来,Bob也生成自己的公钥私钥,将公钥发给Alice,并且将自己数据加密发给Alice,由Alice这一方完成求交。
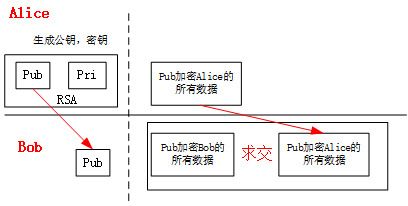
如果反过来,Bob也能生成自己的公钥私钥,然后代替Alice的位置,完成对方的求交
1 不经意传输
不经意传输是一种密码学协议,实现了发送方将潜在的许多信息中的一个传递给接收方,但是对接收方所接收的信息保持未知。
即发送方会发送多个数据,但是不知道接收方到底接收到哪条了。如下面的隐私比较
2 隐私比较
照着文章里面的顺序,先介绍最简单的情况,即隐私比较,
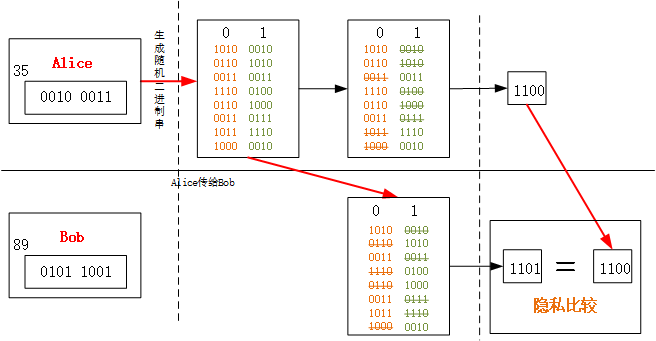
假设Alice和Bob都各只有一个数据分别为\(x\),\(y\),假定\(x\),\(y\)的位数相同,比如\(x:Char\),\(y:Char\),则它们都是8位的表示形式,则\(|x|=|y|=l=8\),如$$35=0010, 0011 $$
1)为Alice的数据\(x\)的每一位都生成2个随机的二进制串(均匀分布),长度为\(n\)(这里举例为4,还能取128,512等等),即\(K_{i,0},K_{i,1}\),且\(i\in\{0,1,2,...,l-1\}\),且\(|K_{i,0}|=|K_{i,1}|=n\)
2)现在Alice为发送方,Bob为接收方,开始执行1/2不经意传输,将Alice生成的\(K\)全部发送给Bob;
3)Bob根据\(y\)的每一位\(y_i\),选择K_{i,0}\(,或者\)K_{i,1}\(,因为\)y\(长度也为\)l\(,则将这\)l$个选择的二进制串进行异或操作,即
4)Alice自己在内部也根据\(x\)的每一位选择一个二进制串,然后将这\(l\)个二进制串进行异或,得到\(K_x\)
5)Alice将\(K_x\)发送给Bob,
6)Bob将收到的\(K_x\)与自己的\(K_y\)进行比较,即可知道自己的数据与Alice的是相等还是不等
3 不经意伪随机函数
从章节2中可得知,Alice持有一组二进制串\(K_{i,0},K_{i,1}\),且\(i\in\{0,1,2,...,l-1\}\),可想而知如果数据量大,假设Alice有\(m_A\)个数据,每个数据生成\(2l\)个二进制串,每个二进制串位数为\(n\),则共传输\(m_A*2l*n\)比特位的数据,其中
- \(l\)是固定的,常量;
- \(n\)需要判断,如果过小,则容易导致冲突(和hash冲突差不多意思),如果过大则太浪费存储和计算量;
重点是,Bob收到后,每一个数据都得去挨个的和Alice的数据做匹配,则需要组合量\(m_A*m_B\)。在传输上,可以不传输随机二进制串,直接传输随机函数种子,让生成随机二进制串的工作放在Alice和Bob两边,因为种子一样,故而生成的后续伪随机二进制串也是一样的。且一个数据只传一个种子,而不是\(2l\)个\(n\)位的二进制串。
因为采用了不经意传输的概念(即Alice传多个,Bob收到自己要的部分信息,而Alice不知道Bob收到了啥)和伪随机函数的组合,所以这种方式就叫做不经意伪随机函数(Oblivious Pseudorandom Function, OPRF)。
4 使用不经意伪随机函数进行PSI
其实就是将章节2中的,假设Alice有一组数据\(X,m_A=100\),Bob有一组数据\(Y,m_B=300\)则
此处有2种形式:
方案一)Alice生成\(m_A\)个种子;
1)Alice生成\(m_A\)个伪随机函数种子\(r_i,i\in \{0,1,2,m_A-1\}\);
2)Alice将这\(m_A\)个伪随机函数种子传给Bob;如章节2,每个数据最终其实是通过异或生成一个新的二进制串,即可认为是一一对应,\(F(r_i,x_i)=K_{x_i}\)
3)则Alice为\(X\)中每一个\(x\)执行对应伪随机函数,最终得到一个集合\(H_A=\{F(r_i,x_i)|i\in \{0,1,...m_A-1\}\}\),大小也为\(m_A\)个元素;
4)Bob需要遍历,每个元素\(y_i\)都得到一个集合\(H_{B_j}=\{F(r_i,y_j)|i\in \{0,1,...m_A-1\} \}\),大小也为\(m_A\)个元素;共需执行\(m_B\)次,则\(H_B=\{F(r_i,y_j)|i\in \{0,1,...m_A-1\} ,j\in\{0,1,...m_B-1\}\}\),最终大小为\(m_B*m_A\)个元素;
5)Alice将\(m_A\)个数据发给Bob,Bob针对自己每个元素生成的集合即\(H_{B_j}\),都需要与整个Alice数据\(H_A\)做比较需要比较,为\(O(m^2)\),然后Bob有\(m_B\)个元素,则复杂度为\(O(m^3)\),最终得到交集。
方案二)
1)Alice生成\(m_B\)个伪随机函数种子\(r_i,i\in \{0,1,2,m_B-1\}\);
2)Alice将这\(m_B\)个伪随机函数种子传给Bob;
3)则Bob为\(Y\)中每一个\(y\)执行对应伪随机函数,最终得到一个集合\(H_B=\{F(r_i,y_i)|i\in \{0,1,...m_B-1\}\}\),大小也为\(m_B\)个元素;
4)Alice需要遍历,每个元素\(x_i\)都得到一个集合\(H_{A_j}=\{F(r_i,x_j)|i\in \{0,1,...m_B-1\} \}\),大小也为\(m_B\)个元素;共需执行\(m_A\)次,则\(H_A=\{F(r_i,x_j)|i\in \{0,1,...m_B-1\} ,j\in\{0,1,...m_A-1\}\}\),最终大小为\(m_A*m_B\)个元素;
5)Alice将\(m_A*m_B\)个数据发给Bob,Bob针对自己集合,即\(H_B\)中每个元素,去与\(H_A\)的\(m_A*m_B\)个元素进行判断,最终得到交集。
方案一相比方案二,在数据传输上少不少流量;但是保密性措施上不如方案二,方案二也更加符合不经意传输的概念(即发送一堆过去,而不是发送一一对应的数据过去),本文采用的是方案二。
不过通过布谷鸟哈希,可以将Alice的\(m_A*m_B\)个数据降一个数量级。
4.1 布谷鸟哈希 Cuckoo hashing
如文章这里介绍的:Cuckoo中文名叫布谷鸟,这种鸟有一种即狡猾又贪婪的习性,它不肯自己筑巢, 而是把蛋下到别的鸟巢里,布谷幼鸟天生有一种残忍的动作,幼鸟会拼命把未出生的其它鸟蛋挤出窝巢。借助生物学上这一典故,cuckoo hashing处理碰撞的方法,就是把原来占用位置的这个元素踢走,不过被踢出去的元素还要比鸟蛋幸运,因为它还有一个备用位置可以安置,如果备用位置上 还有人,再把它踢走,如此往复。直到被踢的次数达到一个上限,才确认哈希表已满。布谷鸟哈希最早于2001 年由Rasmus Pagh 和Flemming Friche Rodler 提出。该哈希方法是为了解决哈希冲突的问题而提出,利用较少计算换取了较大空间。它具有占用空间小、查询迅速等特性,可用于Bloom filter 和内存管理。
假定使用布谷鸟哈希,一共有\(w\)条数据,\(b\)个空桶,还有一个额外的存储桶假设存储上限为\(s\),则一共可存\(b+s\)个数据,即\(w<(b+s)\)
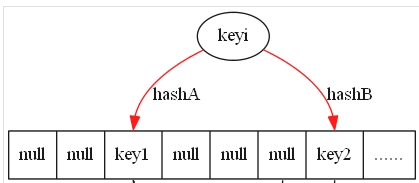
1)首先选择三个哈希,并假定当前元素为x:
\(h_1(x),h_2(x),h_3(x)\),每个hash函数结果都为\({0,...,b-1}\),即映射到这\(b\)个桶中,
2)如果这三个哈希给出的桶\(b_h1,b_h2,b_h3\),如(分别为3,5,7)中有任意个是空的,则存放,当前元素操作结束,退出;否则往下走;
3)如果三个指向的桶都不空,则随机选一个\(b_h1,b_h2,b_h3\)指向的桶,(如\(b_h1=3\),选择第3个),将当前存放在数据\(b_h1\)中的数据\(x^{'}\)赶走,用来存放当前元素x;
4)那针对\(x^{'}\)咋办,循环步骤1),2),3),
5)如果循环到一定次数,还是没解决,那把那个被赶走的数据(此时估计是\(x^{''}\))放到额外的存储桶中。
可以看到,如果\(b\)够大,其实不需要存储桶,不过这需要权衡
图例如下,这里引用百科来解释,且只用到2个hash:
1)如果2个hash都有空位,则随便选一个
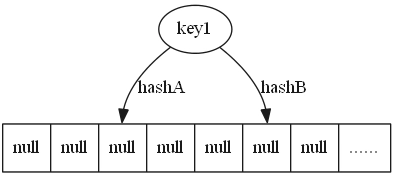
2)插入后

3)再来一个数据,还是有空位
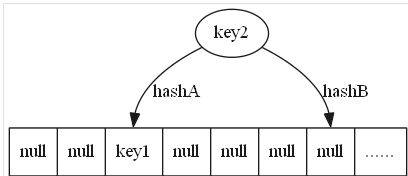
4)插入后

5)再来一个数据,此时冲突了
6)将对应的那个数据赶走,赶走方式是通过对其重新hash出一个新的位置

7)结果

当然了,布谷鸟hash有几种变形
- 通过增加哈希函数进一步提高空间利用率;
- 另一种是增加哈希表,每个哈希函数对应一个哈希表,每次选择多个张表中空余位置进行放置。三个哈希表可以达到80% 的空间利用率。
4.2 基于布谷鸟哈希的PSI
1)Alice和Bob约定3个哈希函数,Alice有\(m_A\)个数据表示为\(X\),Bob有\(m_B\)个数据表示为\(Y\)
2)Bob创建一个\(1.2*m_B+1\)个桶,其中\(1.2*m_B\)是布谷鸟中一一对应的桶,和一个额外的存储桶,该桶大小为\(s\),即一共可容纳\(1.2m_B+s\)个元素;将Bob的\(Y\)经过布谷鸟哈希放入这\(1.2*m_B+1\)个桶中。并将空余部分用假数据填充;
3)Alice生成\(1.2m_B+s\)个伪随机种子,传给Bob;
4)Bob通过一一对应按顺序生成对应的伪随机二进制串,即如果元素在第\(i\)个桶中,则\(F(r_i,y_i)|i\in\{0,1,...,1.2m_B-1\}\);如果元素在存储桶中第\(j\)个位置,则\(F(r_j,y_j)|j\in\{0,1,...,s-1\}\),即Bob一共生成\(1.2m_B+s\)个结果
5)Alice用这\(1.2m_B+s\)个伪随机种子,在自己数据\(X\)上,基于选择的3个hash函数,生成2个集合,
即\(H\)共有\(3m_A\)个元素
和
即\(S\)共有\(s*m_A\)个元素
6)Alice将\(H\)集合打乱顺序,将\(S\)集合打乱顺序,然后分为2个独立的集合发给Bob;所以一共需要发送\((3+s)*m_A\)个元素;
7)Bob可以将其每个元素先在\(S\)集合中查找,如果没有则去\(H\)中查找,如果还没有,则当前元素不在Alice中,
8)Bob得到交集;
从上述步骤6中可发现,基于布谷鸟hash,比之前传输更少。




