Generative Adversarial Nets[Theory&MSE]

---

本文来自《deep multi-scale video prediction beyond mean square error》，时间线为2015年11月，LeCun等人的作品。
从一个视频序列中预测未来的图像帧涉及到构建一个内部表征，该表征能够对准确对图片帧演化（如图像内容和动态）进行建模。这就是为什么像素空间的视频预测主要是通过无监督特征学习来完成。虽然光流在CV领域已经研究的很成熟了，却很少用在未来图像帧预测中。许多视觉应用可以通过视频的下一帧来获取信息，且不需要对每个像素轨迹进行追踪。本文中，作者训练一个卷积网络基于输入的序列去生成未来图像帧。为了解决MSE loss函数带来的图片帧模糊问题，作者提出了三个不同且完毕的特征学习策略：

• 一个多尺度结构；
• 一个对抗训练方法；
• 一个图像梯度差loss函数。

0 引言

视频表征的无监督特征学习是一个很有前景的研究方向，因为数据集基本是无限的，且目前进展仍不尽如人意。相比于经典的图像重构问题，预测未来图像帧甚至需要在缺失其他约束条件下（如稀疏性）构建准确，非平凡的内部表征。因此，该系统预测的越好，那么就需要越强的特征表征。《Unsupervised learning of video representations using LSTM》中通过构建预测图像序列下一个图片帧的系统，学到的表征能够提升在两个动作识别数据集上的分类结果。

本文主要关注直接在像素空间中进行预测，主要处理预测图像中边缘不够清晰明显的问题。通过评估不同的loss函数，发现生成对抗学习可以成功的预测下一帧，最终基于图像梯度生成一个新的loss，旨在保持边缘的清晰度。

1 模型

本部分描述不同的模型结构（单一的，多尺度的，对抗的）和图像梯度差loss（image gradient difference loss）函数。

令\(Y=\{Y_1,...,Y^n\}\)是需要预测的帧序列，输入的视频帧序列为\(X=\{X^1,...,X^m\}\)。构建一个卷积网络，其中卷积和ReLU交替出现。

如图1所示，其是GAN中的G（生成）模块，通过最小化距离函数基于拼接的输入帧\(X\)，预测一个或多个拼接的帧\(Y\)。其中假设基于预测帧和真实帧之间的距离是\(\ell_p\)(p=1或者2)：

\[\mathcal{L}_p(X,Y)=\ell_p(G(X),Y)=||G(X)-Y||_p^p \]

然而，这样的网络至少有两个主要不足：

• 问题1：受限于核的size，卷积操作只有短时依赖。池化的选择也是一种策略，因为输出分辨率必须与输入分辨率一致。有许多保持长时依赖且需要避免池化/子采样导致分辨率减小的方法。最简单也是最老的方法就是去掉池化/子采样；或者通过使用“skip”连接跳过池化层，从而保留高频信息；还有在拉普拉斯金字塔重建过程中线性地组合多个尺度，本文就是采用该方法。
• 问题2：相比于较小程度的\(\ell_1\)，使用\(\ell_2\) loss会生成模糊的预测，当预测更远的帧时效果会越来越坏。假设输出像素的概率分布有2个相似的模型\(v_1\),\(v_2\)，即使\(v_{avg}\)的概率值非常低，值\(v_{avg}=(v_1+v_2)/2\)也会最大限度减小\(\ell_2\) loss。而在\(\ell_1\)范数下，该影响就减小很多了，不过也不是消失，输出值将会同样可能值集合的中位数。

1.1 多尺度网络

关于上述问题1，首先将模型变成多尺度的：让\(s_1,...,s_{N_{scales}}\,\)表示网络输入的size。在本文中，\(s_1=4\times 4,s_2=8\times 8,s_3=16\times 16,s_4=32\times 32\)。\(u_k\)表示朝着size \(s_k\)方向的上缩放因子。令\(X_k^i,Y_k^i\)表示关于size \(s_k\)的\(X^i,Y^i\)的下缩放，且\(G_k^{'}\)是一个网络，给定输入\(X_k\)和粗粒度预测值\(Y_k\)基础上，预测\(Y_k-u_k(Y_{k-1})\)。通过循环定义\(G_k\)，关于\(s_k\)的预测\(\hat Y_k\)为：

\[\hat Y_k=G_k(X)=u_k(\hat Y_{k-1})+G_k^{'}\left( X_k,u_k(\hat Y_{k-1}) \right) \]

因此，网络就预测了一系列结果，从最低的分辨率开始，使用\(s_k\)的预测结果作为起始点，让预测结果的size变成\(s_{k+1}\)。在最低尺度\(s_1\)，网络直需要\(X_1\)作为输入。结构如图2。

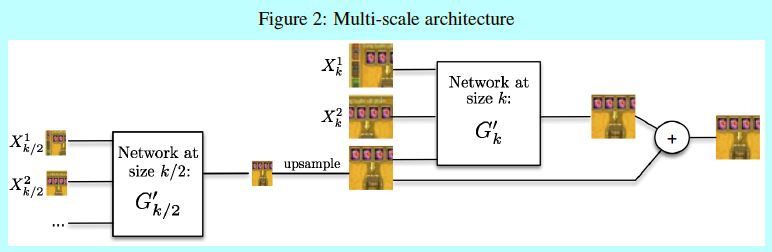
图2 具体细节下面介绍。令可训练的参数为\(W_G\)，通过SGD进行训练。且不论多尺度结构，这里基于\(X\)进行\(Y\)的搜索并没有关于任何可能的假设，当然也会导致模糊预测。因为问题2还没解决。即图像梯度差loss。

1.2 对抗训练

GAN的原理这里就不介绍了。本文作者采用了这种对抗的方式开完成无监督训练的帧预测目的。这里先介绍判别器D，后续再介绍生成器G。判别器D接收图像帧序列，然后预测最后一帧是生成器G生成的概率。注意到这里只判别最后一帧是否是G生成的，而其他帧总是来自数据集的，这让判别器D能够使用时序信息，所以G也要生成关于输入图片帧序列时序相关的图片帧。因为G是一输入帧\(X\)为条件，即使没有噪音的情况下，生成器的输入也会存在变化，所以噪音在这里就不是必须项了。作者在有和没有噪音两个情况下做的实验也证实了基本没差别。所以后续实验就采用没有随机噪音的方式。

为什么使用对抗loss的直观想法是：理论上，为了解决问题2。假设帧序列\(X=(X^1,...X^m)\)，后续帧可以是\(Y=(Y^1,...,Y^n)\)或者\(Y^{'}=(Y^{'1},...,Y^{'n})\)，且两个序列概率相同。如之前所述，基于\(\ell_2\) loss训练的网络可以预测生成平均帧\(Y_{avg}=(Y+Y^{'})/2\)。然而，序列\((X,Y_{avg})\)是基于帧\(X\)并后续跟着\(Y_{avg}\)组成的，其并不是一个可能的序列，所以判别器D可以很容易的进行判别，即模型D并不需要去判别其是属于序列\((X,Y)\)还是序列\((X,Y^{'})\)。

判别器模型D是一个只有单一标量输出的多尺度卷积网络。训练\((G,D)\)包含2个交替的过程。为了简洁，假设使用纯粹的SGD(batchsize=1)进行训练（batchsize=M的情况就是将这M个样本的loss相加）。

训练D
令\((X,Y)\)表示数据集中样本，其中\(X\)是一个包含m帧的图像序列，而\(Y\)是包含n帧的图像序列。需要训练一个判别器D去准确区分\((X,Y)\)是正类，而\((X,G(X))\)是负类。详细点说，对每个尺度\(k\)，先将生成器G固定，对\(D_k\)进行一次SGD迭代。此时有监督样本是类1的\((X_k,Y_k)\)和类0的\((X_k,G_k(X_k))\)。因此，训练D的loss函数为：

\[\mathcal{L}_{adv}^D(X,Y)=\sum_{k=1}^{N_{scales}}\, L_{bce}(D_k(X_k,Y_k),1)+L_{bce}(D_k(X_k,G_k(X_k)),0) \]

其中\(L_{bce}\)是二值交叉熵（binary cross-entropy，bce）loss，定义如下：

\[L_{bce}(Y,\hat Y)=-\sum_i\hat Y_i \log(Y_i)+(1-\hat Y_i)\log (1-Y_i) \]

这里\(Y_i\)取值为\(\{0,1\}\),而\(\hat Y_i\)取值为\([0,1]\)。

训练G
令\((X,Y)\)表示不同的数据样本，此时保持判别器D固定，对生成器G执行一次SGD迭代，以最小化对抗loss：

\[\mathcal{L}_{adv}^G(X,Y)=\sum_{k=1}^{N_{scales}}L_{bce}(D_k(X_k,G_k(X_k)),1) \]

最小化这个loss意味着让生成器G生成的数据能让判别器D变得混乱，即D不能正确的进行判别G生成的结果。然而实际上，只最小化该loss会导致不稳定。G总是生成能够混乱D的样本，可是却并不足够靠近\(Y\)（即，生成的样本是足够让D以假乱真，可是生成的样本对人类没多大意义）。然后，D会学着判别这些样本，导致G生成其他混乱的样本，然后一直循环。为了解决这个问题，需要在生成器上增加一个loss，即成为一个组合loss。此时生成器G的loss为\(\lambda_{adv}\mathcal{L}_{adv}^G+\lambda_{\ell_p}\mathcal{L}_p\)。这自然引入了一个均衡超参数，即介于是边缘锐化还是GAN的对抗原则，该过程在下面算法1详细介绍。

1.3 图像梯度差loss（Image Gradient Difference Loss，GDL）

另一个锐化图像边缘的策略是直接在生成的loss函数中对预测的图像梯度差进行惩罚。这里定义一个新的loss，梯度差loss（gradient difference loss，GDL），且其与对抗loss结合起来。GDL函数是介于ground-truth图像\(Y\)和预测图像\(G(X)=\hat Y\)之间的：

\[\mathcal{L}_{gdl}(X,Y)=L_{gdl}(\hat Y,Y)=\sum_{i,j}\left ||Y_{i,j}-Y_{i-1,j}|-|\hat Y_{i,j}-\hat Y_{i-1,j}|\right|^\alpha+\left ||Y_{i,j-1}-Y_{i,j}|-|\hat Y_{i,j-1}-\hat Y_{i,j}|\right |^\alpha \]

这里\(\alpha\)是一个整数或者等于1，\(|\cdot|\)表示绝对值。
本文相对同类论文优势：

• 相对于其他人总的变化只考虑输入的重构帧，本文基于预测和真实值之间梯度差进行loss惩罚；
• 选择最简单可能的图像梯度，只涉及到近邻的像素强度差异，并不考虑更广的邻居，让训练时间降低。

1.4 结合后的loss

在本文中，结合后的生成器最终loss如下：

\[\mathcal{L}(X,Y)=\lambda_{adv}\mathcal{L}_{adv}^G(X,Y)+\lambda_{\ell_p}\mathcal{L}_p(X,Y)+\lambda_{gdl}\mathcal{L}_{gdl}(X,Y) \]

2 实验

本文基于UCF101和Sports 1m数据集，基于2个参数配置：

• 使用4个输入帧预测一帧未来帧，并将预测帧作为下一个真实数据来循环生成后续未来帧；
• 使用8帧输入帧同时预测8帧未来帧。该方法明显是个更困难的问题。

使用Sports1m作为训练集，因为UCF101只有图片上部分位置才有变化，剩下的就和固定的背景一样。通过随机选择一个范围内时序图像帧，基于32x32的块，并确定有足够的变化（基于帧之间进行L2计算来判断）。数据块首先进行归一化，保证值范围在-1和1之间。

2.1 网络结构

基于好几个模型进行实验，不过只有在最开始的时候是这样，后续都是基于多尺度结构。本文的baseline模型使用L1和L2的loss，GDL-L1（或者GDL-L2）模型是在GDL上\(\alpha=1\)(对应\(\alpha=2\))和\(p=1\)(对应\(p=2\))的loss，相对的超参数\(\lambda_{gdl}=\lambda_{\ell_p}=1\)。对抗模型（Adv）采用的对抗loss，其\(p=2\)，且\(\lambda_{adv}=0.05,\lambda_{\ell_p}=1\)。最后Adv+GDL模型是二者结合，基于同样的参数下\(\alpha=1,\lambda_{gdl}=1\)。

生成模型的训练
生成模型G结构如表1

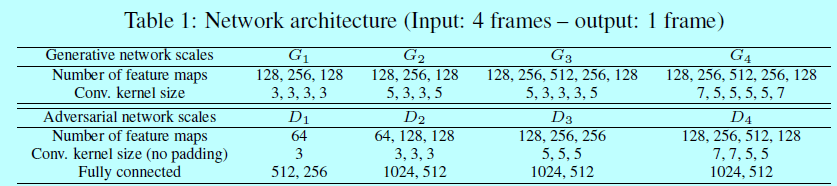
其包含padded卷积和ReLU激活函数。在模型最后增加Tanh保证输出结果在-1和1之间。学习率$\rho_G $开始是0.04，然后随着时间降到0.005。为了发挥GPU硬件显存，在对抗学习中minibatch为4或者8。基于小图像块进行训练，不过因为是全卷积的，所以可以预测的时候无缝应用在更大图片上。

对抗训练
判别器D也在表1中，使用标准的非padded卷积，然后跟着全连接层和ReLU激活函数。对于最大的尺度\(s_4\)，在卷积后面加了一个2x2的池化。网络训练的时候学习率\(\rho_D=0.02\)

2.2 质量评估

。