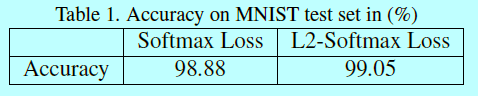face recognition[angular/consine-margin-based][L2-Softmax]
本文来自《L2-constrained Softmax Loss for Discriminative Face Verification》,时间线为2017年6月。
近些年,人脸验证的性能因引入了深度卷积网络而提升很大。一个典型的人脸识别流程就是:
- 训练一个基于softmax loss的深度卷积网络;
- 提取倒数第二层作为每个样本图片的特征表征;
- 基于两个样本的表征向量,计算cos的向量相似度。
softmax本身并不会让两个正样本对的相似度得分优化的更大,两个负样本对的相似度得分优化的更小。而实际需要中,需要构建具有类内紧凑性和类间可分性的特征,这会存在瓶颈,所以需要在loss上增加一些类似正则项的东西。本文中,作者在特征表征层加入\(L_2\)约束,意图让该样本落在一个固定半径的超球面表面。该模型可以很容易的基于现有的深度学习框架实现。通过在训练集整合该简单步骤,明显能够提升人脸验证的性能。特别的,在IJB-A上的True Accept Rate为0.909,False Accept Rate为0.0001。
近些年,人脸识别上也有不少出色的工作,其主要从2个角度解决人脸验证上的问题:
- 将人脸图片对输入到训练算法中,并获得embedding向量,在该向量中,正对(相同ID的人脸)会更靠近,负对(不同ID的人脸)会更远离。如《Learning a similarity metric discriminatively, with application to face verification》《Discriminative deep metric learning for face verification in the wild.》,FaceNet等等;
- 将人脸图片和对应的ID label一起用来训练辨识性的特征。大多数现有方法是先基于softmax loss训练一个DCNN,然后这些特征后续直接计算人脸对的相似性得分或者用来训练得到辨识性度量embedding;另一个策略是联合识别-验证来多任务训练网络。
最近提出的center loss可以学到更具辨识性的人脸特征。不过L2-norm softmax不同的是:
- 本方法只用一个loss函数,而center loss要联合softmax一起训练;
- center loss在训练中会引入额外的CxD参数,这里C是类别个数,D是特征维度;另一方面,L2-norm softmax定义中 只引入一个超参数。同时可以将L2-norm softmax 与center loss一起联合训练。
0 引言
在无约束条件下进行人脸验证依然是一个挑战,因为仍然很难去处理视角,分辨率,遮挡和图像质量等变化极大的问题。训练集中数据质量的非平衡性也是造成上述性能瓶颈的原因之一。现有的人脸识别训练样本数据集包含大量高质量的正脸图片,而无约束和难分辨的人脸数据较少。大多是基于DCNN的模型都是基于softmax训练的,可是该模型倾向于对高质量图片过拟合,所以就没法正确区分困难场景下的人脸。
当然使用softmax 训练人脸验证也有其优缺点:
- 一方面,它可以很容易的用现有的深度学习框架去实现,而且不同于triplet loss等,softmax不需要在输入batchsize上做任何限制,而且收敛也快。学到的特征对于人脸验证而言具有足够的辨识性,且不需要额外的度量学习(metric learning);
- 另一方面,softmax对于样本分布是有偏的。不同于contrastive loss和triplet loss,它们是特定寻找难样本,而softmax loss就是最大化给定mini-batch下所有样本的条件概率,因此,softmax能够很好的拟合高质量人脸,却忽略了整个mini-batch中很少出现的困难脸。
作者受到《Deep convolutional neural network features and the original image》的启发,带有L2-norm的softmax已经带有足够图片质量的信息:
- 高质量的正脸特征的L2-norm很高,同时模糊且姿态特异的人脸的L2-norm很小,如图1b
- 更甚,softmax loss不会特定优化人脸验证的需求(即,相同ID的人脸更靠近,不同ID的人脸更远离)。正是基于这个原因,许多方法在softmax特征部分采用度量学习《Unconstrained face verification using deep cnn features》,《Deep face recognition》,《Triplet probabilistic embedding for face verification and clustering》或者在softmax loss上增加辅助loss《Deeply learned face representations are sparse, selective, and robust》,《Latent factor guided convolutional neural networks for age-invariant face recognition》,《A discriminative feature learning approach for deep face recognition》。
本文提出一个针对softmax loss的策略,作者期望在训练中,在特征上增加一个约束,如L2-norm。换句话说,是期望将特征约束在一个固定半径的超球面表面,提出的L2-softmax有2个优势:
- 同时关注高质量和低质量的人脸,因为此时所有特征都都有相同的L2-norm;
- 它通过在规范化空间(normalized space)中更严格的让相同ID的特征更靠近,不同ID的特征更远离来增强人脸验证信息。
因此,它最大化了负对(不同ID的人脸)和正对(相同ID的人脸)之间的规范化L2距离或余弦相似性得分的边际。因此,它克服了常规softmax loss的主要缺点。不过它同时保留了常规softmax loss的优势:一个网络结构,一个loss体系,不需要联合监督(多任务学习,正则项等等方式),其本身可以很容易的基于现有的深度学习框架去编写,而且收敛也很快。它对网络只是引入一个标量。相比于常规softmax loss,L2-norm softmax在性能加速上有明显提升。且在几个比赛上比那些多网络或者多loss的模型更好。本文贡献:
- 提出一个简单,新颖,高效的L2-softmax,且能将特征表征约束到一个标量\(\alpha\);
- 研究不同性能变化与尺度参数\(\alpha\)之间的关系,并提供合适的边际,以获取稳定的高性能;
- 在所有比赛上获得了一致,明显的加速。
1 背景
先概述下使用DCNN训练一个人脸验证系统的流程。
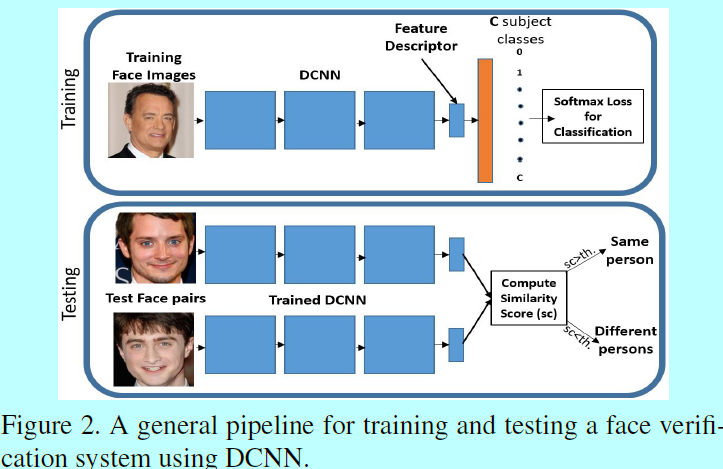
给定一个包含人脸和对应ID的训练数据集,先训练一个DCNN用作分类,该网络此时学到如何将一张给定的人脸图片分到对应的ID。softmax loss式子如:

这里M是batch-size,\(\mathbf{x}_i\)是该batch中第\(i\)个输入样本,\(f(\mathbf{x}_i)\)是DCNN倒数第二层的输出,\(y_i\)是对应的类别,\(W,b\)是网络最后一层(扮演着分类器角色)的权重和偏置。
在预测的时候,用\(f(\mathbf{x}_g)\)和\(f(\mathbf{x}_p)\)表示测试图片\(\mathbf{x}_g\),\(\mathbf{x}_p\)经过DCNN得到的特征描述,并经过归一化到单位模(length=1)。然后,在这两个特征描述上,使用一个距离度量去计算在嵌入空间中它们之间的相似度得分。如果该得分超过一个设定的阈值,那么就判定这2张图片来自同一ID。而常用的计算距离度量的就是L2距离或者是cos距离如式子2。

上述流程中隐含2个主要问题:
- 人脸验证中训练和预测是分开的。用softmax做训练不论是在规范化还是角度空间中,都不会倾向于正对相距更近,负对相距更远(即本身没这种正则惩罚);
- softmax分类器在对困难或者极端样本建模时候是很弱的。如在经典的训练batch中,且当前batch是数据质量不平衡的,softmax可以通过增加容易样本的L2-norm,并忽略难样本,从而达到最小化。网络因此通过特征描述的L2-norm来响应人脸的质量。为了验证这个理论,作者在IJB-A上做了个实验。首先将该数据集中templates(同一个ID的图片/帧组,groups of images/frames of same subject)基于各自特征描述(这些特征都是使用Face-Resnet通过常规softmax训练得到的)的L2-norm分成3个不同的子集:
- L2-norm < 90归类到集合1;
- 90< L2-norm <150归类到集合2;
- L2-norm< 150归类到集合3.
它们总共形成6组评估对。图1a描述了这6对的结果,可以很容易发现当两个templates的L2-norm都很小的时候,效果是很差的。而如果一对中两个的L2-norm都很大,那么效果是最好的。不同组之间的结果差距还是很明显的。图1b展示了集合1,集合2,集合3中的一些样本templates,可以发现L2-norm透露着图片质量信息。
所以作者让每个人脸图片的L2-norm都是固定的。即增加一个L2约束到特征描述上,从而强制每个特征都处在一个固定半径的超球面上。该方法有2个优势:
- 在超球面上,最小化softmax等效于最大化正对之间的cos相似度同时最小化负对之间的cos相似度,从而强调特征的验证信息;
- softmax loss可以更好的对极端或者困难人脸进行建模,因为此时所有的人脸特征都有相同L2-norm。
2 \(L_2\) softmax loss
提出的L2-softmax式子如:

这里\(\mathbf{x}_i\)是大小为M的mini-batch中的一个输入,\(y_i\)是对应的类别标签,\(f(\mathbf{x}_i)\)是从DCNN倒数第二层获取的特征描述,C是类别个数,\(W,b\)是将最后一层扮演成分类器的网络权重和偏置。该等式相比于式子增加了一个约束项。下面用MNIST来展示该约束的效果。
2.1 基于mnist
作者在MNIST上研究了L2-softmax的效果,首先采用的是比LeNet5更深更宽的网络结构,其中最后一层隐藏层神经元设为2,方便可视化,并做了一组对照实验:
- 使用常规softmax进行end-to-end的训练;
- 在最后的2维空间上,增加一个L2-norm层和scale层,即式子3的描述。
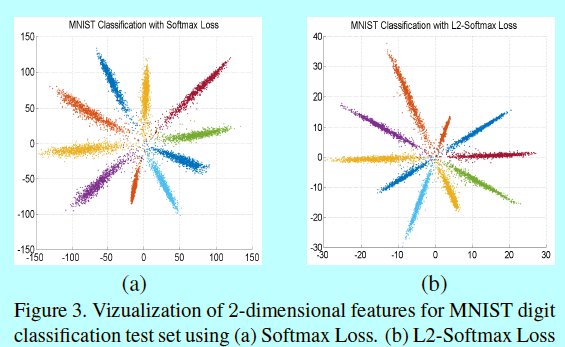
图3描述了MNIST中1w个测试样本,不同类的2D特征,每个点表示一个样本。第二个对照实验使用的向量是来自L2-norm层之前的输出
作者在上面对照实验中发现两个很清晰的不同点:
- 当使用常规softmax,类内角度变化会更大,这可以通过每个叶片(形象描述)的平均宽度来计算。L2-softmax获取的特征类内角度变化是更小的;
- 更大的特征范数,会让一个能够正确分类的类别获得更大的概率。所以softmax的特征幅值要更大(都快到150了)。然而在L2-softmax中,特征范数的影响却很小,因为每个特征都在计算loss之前被归一化到固定半径的园上了。因此网络重点会在规范化或者角度空间中,将来自同一个ID的特征互相靠近,并让来自不同ID的特征相互远离 。
ps:值得注意的是,这里基于经典DCNN并将图片映射到2维空间。
2.2 实现细节
这里提供基于DCNN,式子3的实现细节。该约束是通过增加一个L2-norm层和scale层实现的:

该模块就是简单添加到原始带有softmax的DCNN倒数第二层之后,softmax层之前。

L2-norm层通过式子4归一化输入特征\(\mathbf{x}\)到单元向量上。scale层如式子5,通过一个参数\(\alpha\)将输入向量尺度缩放到固定半径上。也就是总的来说,引入了一个标量参数\(\alpha\),而它可以通过网络其他参数一起训练。
该模块是全可微分的,可以用在end-to-end的网络训练中。在预测阶段,该模块是冗余的,因为在计算cos相似度的时候,本身特征向量就需要归一化到单位模(unit length)。在训练阶段,梯度会反向经过L2-norm和scale层。通过链式法则计算关于\(\alpha\)的梯度如下:

2.3 参数分析
如上所述,\(\alpha\)扮演着关键角色。即有2种方法来增强L2-norm约束:
- 在整个训练过程中保持\(\alpha\)不变;
- 让网络自己学习\(\alpha\)。
第二个方法相对优雅而且也能保证数据驱动,从而总是能够在常规softmax上提升效果。但是网络学到的\(\alpha\)很大,会导致一个相对宽松的L2-约束。softmax分类器意在最小化总的loss下增大特征范数,现在是增大\(\alpha\),会让网络更自由的去拟合容易的样本。所以由网络学习的\(\alpha\)可以看成是该参数的上限。所以一个更好的性能就是将\(\alpha\)固定到一个相对更低的常量。
不过另一方面,\(\alpha\)如果很小,训练就不会收敛,例如\(\alpha=1\)在LFW上效果就很差,只有86.37%的准确度。
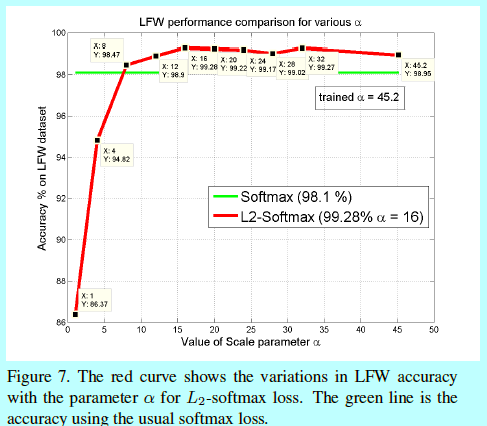
原因猜测是如果基于一个小的半径的超球面,其超球面的面积更受限,来自同一个类的样本和不同类的样本的分布就相对没更大半径超球面要容易区分。
因此,需要计算得到\(\alpha\)的下界。假设类别个数C有2倍小于特征维度D,那么可以在维度D的超球面上进行分布,保证任意2个类的中心相距90度。
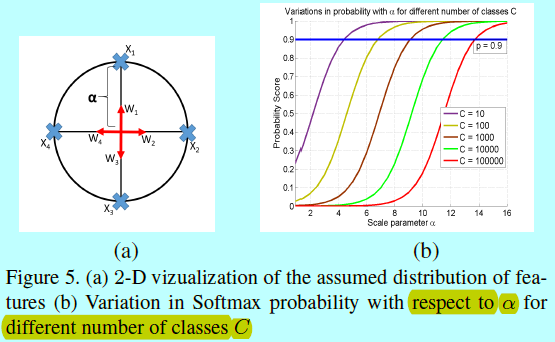
如图5a,表示在一个半径为\(\alpha\)的园上分布C=4个类中心。并假设分类器权重\(W_i\)是指向各自类别中心方向上的单元向量,并忽略偏置。
正确对一个特征进行分类的平均softmax分类概率\(p\)为:
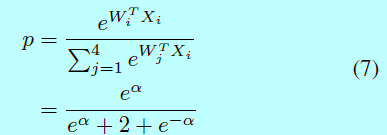
忽略项\(e^{-\alpha}\),然后将类别泛化到C类,平均概率为:

图5b中可以发现,在给定分类概率(p=0.9)下,C更大,那么\(\alpha\)就需要更大。给定类别C,可以通过下面式子获得\(\alpha\)的下界

3 实验及分析
作者前面DCNN用的是Face-ResNet,其结构为:
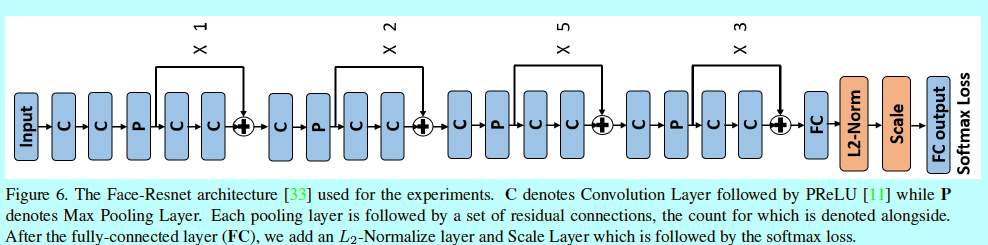
基于caffe实现。
3.1 基于小数据集
3.2 基于大数据集
3.3 基于不同DCNN
3.4 基于辅助的loss

3.5 和现有方法对比