face recognition[Euclidean-distance-based loss][Center Face]

---

本文来自《A Discriminative Feature Learning Approach for Deep Face Recognition》，时间线为2016年。采用的loss是Center loss。

0 引言

通常使用CNN进行特征学习和标签预测的架构，都是将输入数据映射到深度特征（最后一层隐藏层的输出），然后到预测的标签，如图1.

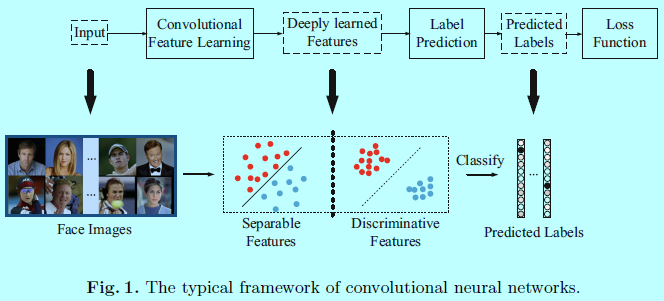
在通用目标，场景和动作识别中，预测的样本归属的类别也处在训练集中，这被称为“闭集识别”。因此，预测的标签能表示模型的性能，且softmax loss可以直接处理分类问题。这时候，标签预测问题就类似一个线性分类模型，且深度学到的特征也具有可分性。

而对于人脸识别任务来说，学到的深度特征不止具有可分性，也具有辨识性。因为不可能在训练集中收集到所有预测的ID类别，CNN输出的特征并不总是可用的。需要让训练出来的特征具有辨识性，且能够足够泛化到那些未见过的人ID的类别。辨识性即需要特征能够保证类内变化的紧凑性和类间不同的可分性。如图1所示，辨识性特征可以很容易的通过KNN去划分。然而，softmax loss只保证了特征的可分性，生成的特征还不足够用于人脸识别。

在CNN中，构建让特征具有高度辩识性的loss函数是很有意义的。在CNN中的SGD通常是基于mini-batch，其不能很好的反映深度特征的全局分布。因为训练集本身很大，也没法每次迭代的时候把整个训练集都放进去迭代。作为一种解决方法，contrastive loss和triplet loss各自构建了基于图片二元组和图片三元组构建loss函数。然而相比于图片样本，需要投入的训练图片二元组和三元组的数量会急剧增长，同时也不可避免的会减慢收敛和增大不稳定性。通过仔细的选择图片二元组和三元组，虽然这些问题可以部分解决。不过也明显增加了计算复杂度，且也让训练过程变得不够方便。

这里作者提出了一个新的loss函数，叫center loss，可以有效的增强深度特征的辨识性。特别的，对每个类别的深度特征，会学到一个中心（和特征有着一样维度的一个向量）。在训练中，会同时更新该中心，且最小化深度特征与对应中心向量的距离。所以该CNN是基于softmax loss和center loss联合训练的，通过一个超参数去权衡这两个loss。直观的，softmax loss强制不同类别的深度特征保持分离。center loss有效的将同一个类别的其他特征往其对应的中心紧推。通过联合训练，不止让类间特征的区别变大，同时让类内特征的变化减小。因此让学到的深度特征辨识性可以增强。

1 Center Face

这里先通过一个例子介绍下深度特征的分布，然后基于该分布提出了center loss来提升深度特征的辨识性。

1.1 简单的例子介绍深度特征的分布

本部分是基于MNIST数据集进行呈现的。通过将LeNet网络修改的更深更宽，不过减少最后一层隐藏层的神经元个数为2（即学到的深度特征维度为2）。所以可以直接在2D坐标系上呈现学到的特征。网络结构的详细部分如表1。

softmax loss函数式子为：

\[L_s=-\sum_{i=1}^m\log \frac{e^{\left ( W_{y_i}^T \, \mathbf{x}_i+b_{y_i}\right )}}{\sum_{j=1}^n e^{\left ( W_j^T\, \mathbf{x}_j+b_j\right )}} \]

其中，\(\mathbf{x}_i\in R^d\)表示第\(i\)个深度特征，属于\(y_i\)类，\(d\)是特征的维度。\(W_j\in R^d\)表示最后一层全连接层中权重\(W\in R^{d\times n}\)矩阵的第\(j\)列，\(\mathbf{b}\inR^n\)是对应偏置项。mini-batch的size和类别的个数分别为\(m\)和\(n\)。这里忽略偏置项以简单说明（实际上，忽略了之后，性能也没什么差别）。

生成的2D深度特征如上图所示。因为最后的全连接层表现的和一个线性分类器一样，所以不同类别的深度特征可以通过决策面简单的划分。图2中可以得出：

• 基于softmax loss的监督之下，学到的深度特征具有可分性；
• 深度特征不具有足够的判别性，因为仍然有明显的类内变化

所以还不能直接将softmax学到的特征直接用在人脸识别上。

1.2 Center Loss

所以，如何提出一个有效的loss函数去提升深度特征的辨识性呢？直观的，是减小类内变化的同时保持不同类特征的可分性。所以，这里提出一个center loss函数：

\[L_C=\frac{1}{2}\sum_{i=1}^m||\mathbf{x}_i-\mathbf{c}_{y_i}||_2^2 \]

其中\(\mathbf{c}_{y_i}\in R^d\)表示深度特征的第\(y_i\)个类中心。该式子可以有效的表达类内变化。理想情况下，\(\mathbf{c}_{y_i}\)可以随着深度特征的改变而更新。换句话说，需要将整个训练集都考虑在内，并在每次迭代中对每个类别的特征进行平均，这在实际实践中不具有可操作性。因此，center loss不能直接使用，这也可能就是在CNN中center loss一直没有应用的一个原因吧。
为了解决该问题，提出两个必须的修改：

• 不直接基于整个训练集合更新center，而是基于mini-batch进行操作。在每次迭代中，通过平均对应的类别特征来计算center（这时候，一些center可能并不会被更新）；
• 为了避免误标记样本带来的较大扰动，使用一个标量\(\alpha\)来控制center的学习率。

\(L_C\)关于\(\mathbf{x}_i\)的梯度和更新\(c_{y_i}\)的式子如下：

\[\frac{\partial L_C}{\partial \mathbf{x}_i}=\mathbf{x}_i-\mathbf{c}_{y_i} \]

\[\Delta \mathbf{c}_j=\frac{\sum_{i=1}^m\delta(y_i=j)\cdot (\mathbf{c}_j-\mathbf{x}_i)}{1+\sum_{i=1}^m\delta (y_i=j)} \]

当\(condition\)满足的时候\(\delta (condition)=1\)，反之\(\delta (condition)=0\)，\(\alpha\)取值在[0,1]之间。通过将softmax loss和center loss 联合训练CNN以保证辨识性特征学习，对应的式子为：

\[\begin{align} L&= L_S+\lambda L_C \\ & = -\sum_{i=1}^m\log\frac{e^{\left ( W_{y_i}^T \, \mathbf{x}_i+b_{y_i}\right )}}{\sum_{j=1}^n e^{\left ( W_j^T\, \mathbf{x}_j+b_j\right )}}+\frac{\lambda}{2}\sum_{i=1}^m||\mathbf{x}_i-\mathbf{c}_{y_i}||_2^2 \end{align} \]

可以看到，由center loss监督的CNN是可训练的，可以通过标准SGD进行迭代，标量\(\lambda\)可以用来权衡这两个loss函数。传统的softmax loss可以看成该联合loss的一个特殊情况，即\(\lambda =0\)。

上述流程简单介绍了网络训练的过程。

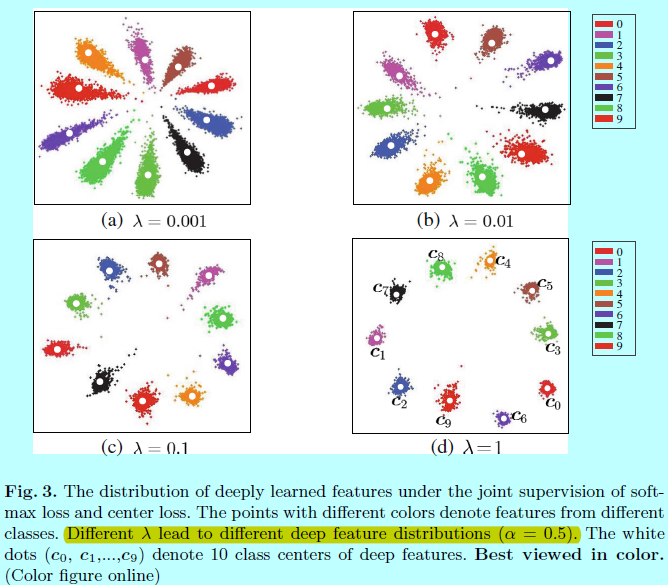
从图3可以发现，不同的\(\lambda\)会导致不同的深度特征分布，在值合适的情况下，深度特征的辨识性可以增强不少。

1.3 讨论

• 如果只是用softmax loss，则会导致较大的类内变化；如果只用center loss，则深度特征和center就会下降为0（此时center loss是很小的）;
• 相比于contrastive loss和triplet loss，它们都需要对数据进行扩展成二元组或者三元组，而center loss不需要对训练样本进行组合操作，因而CNN网络能够更直接的训练。

2 实验及分析

这里介绍下实现的一些细节和个别超参数的影响对比。

2.1 实现细节

• 基于MTCNN先对人脸数据集进行人脸检测和对齐，人脸检测框统一裁剪成112x96大小，然后通过每个像素值减去127.5并处以128进行大致的归一化。
• 使用网络上收集了的数据集如CASIA-WebFace，CACD2000，Celebrity+，在移除了出现在测试集中的ID图片，大概有0.7百万张，17,189个ID。并且做了简单的水平翻转以数据增强。
• 采用caffe库进行实现，网络结构如图
  
  为了公平对比，只在loss函数层做了不同的设定，如softmax loss(model A)；softmax+contrastive（model B）；softmax+center（model C）。这些模型的batchsize都为256，在两块TitianX上完成。对于模型A和模型C，学习率始于0.1，然后在16K和24K迭代次数时分别除以10。大致需要28K次迭代14小时完成整个训练。对于模型B，发现收敛的更慢，其以0.1初始化学习率，然后在24K和36K进行变化。一共42K次迭代，大致22小时。
• 将第一层全连接层的输出作为深度特征，通过提取每个图片的该特征并对图片进行左右翻转并再次提取特征，将这2个特征进行合并以此来表示该图片。先通过PCA进行降维，然后采用cos距离来计算两个特征的距离。最近邻和阈值对比分别用来作为人脸识别和验证。

2.2 基于超参数的实验

超参数\(\lambda\)控制着类内变化，\(\alpha\)控制着模型C中center c的学习率。他们对网络的训练都很重要。

上图中的一个实验是固定\(\alpha=0.5\)并变化\(\lambda\)，可以发现只用softmax(\(\lambda=0\))效果并不好；同样的对于第二个实验，固定\(\lambda=0.003\)，改变\(\alpha\)发现还是挺稳定的。



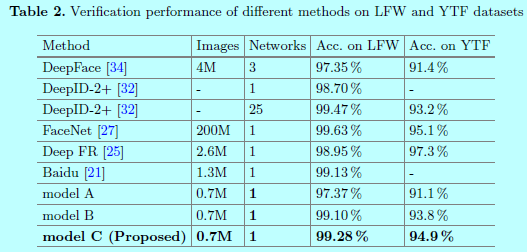
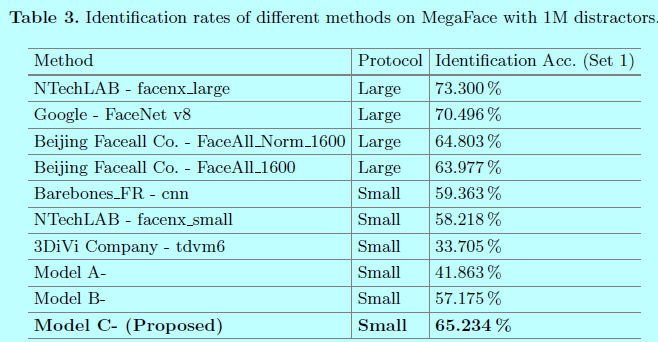
从上图可以发现，在小数据量上，center Face效果还是挺不错的，当然还是干不过谷歌那种包含超大数据量的FaceNet