face alignment[Ordinary Procrustes Analysis]
人脸识别,大致可以分为以下四个步骤:
- 人脸检测:从图片中准确定位到人脸,并以矩形框将其裁剪出来;
- 人脸矫正(对齐): 检测到的人脸,可能角度不是很正,需要使其对齐,比如旋转,缩放;
- 特征提取:对矫正后的人脸进行特征提取,现在做法通常都是基于一个CNN模型;
- 人脸比对:对两张人脸图像提取的特征向量进行对比,计算相似度。
上述第一步,目前主流的做法都来自如Faster RCNN或者SSD等通用目标检测的一些改进网络,大致可以直接将人脸检测就看成特定目标的检测;这里主要介绍人脸校正部分,且介绍其中一种方法,也是MTCNN使用的方法,该方法简单快速,不需要去先建立3D模型然后进行映射。当然该方法效果么,从其原理上,主要解决的依然是正脸的对齐,无法很好解决侧脸的对齐(这时候可以用GAN或者3D建模去恢复)。
0 引言
MTCNN中采用的人脸矫正方法,是假设拿到的人脸几乎都是正脸,不过此时正脸有尺度不等,角度偏移等。而且需要预先设定一个平均脸,即目标脸的位置,标记出平均脸的所有关键点应该处于的位置,然后将所有人脸矫正到该平均脸上。
1 Procrustes Analysis普氏分析法
下述概念部分参考自《Master Opencv...读书笔记》非刚性人脸跟踪 II。
人脸由眼睛、鼻子、嘴巴、下巴等部位构成,正是因为这些部位形状、大小和相对位置的各种变化,才使得人脸表情千差万别,因此可以对这些部位的形状和结构关系进行几何描述,作为人脸表情识别的重要特征。这里,几何关系就是指预定义点集的空间组态模式,而这些点与脸部器官在几何空间存在对应关系(比如眼角、鼻尖、眉毛)。
Facial geometry,通过两种元素的参数化配置组成:
- 全局变形(刚性):指人脸在图像中的分布,允许人脸出现在图像中任意位置,包括人脸的坐标(x,y)、角度、大小;
- 局部变形(非刚性):指不同人和不同表情之间脸部形状的不同,与全局形变不同,人脸的高度结构化特征对局部形变产生了极大的约束。
全局变形可以由二维空间的函数表达,并且可以应用于任何类型的对象;然而局部形变只针对特定目标,需要从训练集中去学习得到。
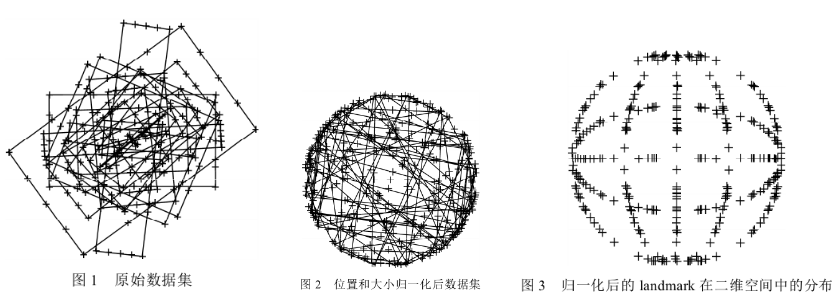
简单的仿射变换包括:平移,旋转,缩放。普氏分析法是一种用来分析形状分布的方法。数学上来讲,就是不断迭代,寻找标准形状(canonical shape),并利用最小二乘法寻找每个样本形状到这个标准形状的仿射变化方式。(可参照维基百科的GPA算法)

图1.1 平移,旋转,缩放的三种仿射变换方式示意
如上图所示,我们假设一张2D图片上每个点都为坐标\((x,y)\),我们对坐标上表示的值不感兴趣,我们只是对其坐标位置感兴趣。这里表现的就是原始目标上每个像素点的仿射映射。
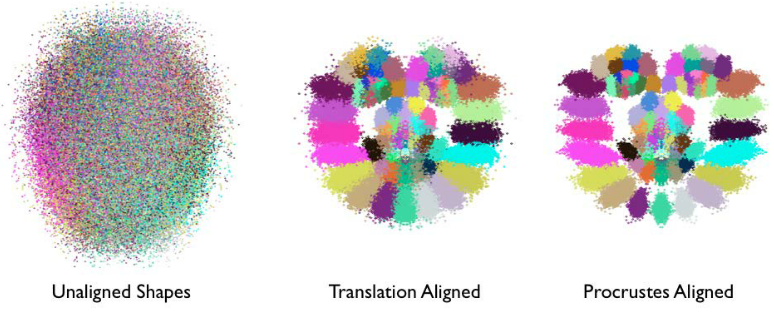
- Procrustes analysis的作用可以看作是一种对原始数据的预处理,目的是为了获取更好的局部变化模型作为后续模型学习的基础。如下图所示:
- 每一个人脸特征点可以用一种单独的颜色表示;
- 经过归一化变化,人脸的结构越来越明显,即脸部特征簇的位置越来越接近他们的平均位置;
- 经过一系列迭代,尺度和旋转的归一化操作,这些特征簇变得更加紧凑,它们的分布越来越能表达人脸表情的变化。【剔除刚性部分、保留柔性部分】
- 下图为不同大小、不同长宽比的矩形,经过归一化过程后,各个样本点分布服从一定概率分布趋势
在图1.1中,将这三种方法合并到一个式子中:
上述式子中\(s\)就是缩放因子,\(\theta\)就是旋转角度,\(t\)表示平移的量,\(R\)是一个正交矩阵\(R^TR=I\)
所以现在问题变成了:如何旋转,平移和缩放第一个向量,使其尽可能对齐第二个向量的点,即通过使用仿射变换将第一个图像进行变换,然后覆盖第二个图像。并判断变换后的第一个图像与第二个图像的距离,并使其距离最小。
假设两个形状矩阵分别为\(p\),\(q\),矩阵每一行表示一个特征点(人脸中即为像素点)的(x,y)坐标,假设有N个特征点坐标,则\(p\in R^{N \times 2}\),\(q\in R^{N \times 2}\)。对应的数学形式为:
求其最小,也就是
其中\(||\cdot||_F\)是Frobenius范数,这里就是L2范数。
在人脸对齐:Procrustes analysis中所述,对两边的点集进行消除平移,消除缩放之后,旋转的角度部分可以变成求解下面式子:
此时根据Ordinary_Procrustes_analysis中的Orthogonal_Procrustes_problem所述,式子解为:
那么仿射变换矩阵为:
2 代码
如switching-eds-with-python第一部分所述:
- 将矩阵数值类型转换成float;
- 每个特征点减去当前形状的中心点,消除平移的影响(一旦找到了处理后的特征点集和的最优缩放因子和角度,这里的中心点c1和c2可以用来找回完整解);
- 每个特征点除以当前形状的尺度因子,消除尺度的缩放影响;
- 使用SVD计算旋转角度;
- 返回一个仿射变换矩阵的完整矩阵。
'''a.py
https://matthewearl.github.io/2015/07/28/switching-eds-with-python/ 中代码是有问题的;
因为numpy的矩阵相乘需要numpy.dot,直接的相乘是逐元素相乘 '''
def transformation_from_points(points1, points2):
'''0 - 先确定是float数据类型 '''
points1 = points1.astype(numpy.float64)
points2 = points2.astype(numpy.float64)
'''1 - 消除平移的影响 '''
c1 = numpy.mean(points1, axis=0)
c2 = numpy.mean(points2, axis=0)
points1 -= c1
points2 -= c2
'''2 - 消除缩放的影响 '''
s1 = numpy.std(points1)
s2 = numpy.std(points2)
points1 /= s1
points2 /= s2
'''3 - 计算矩阵M=BA^T;对矩阵M进行SVD分解;计算得到R '''
# ||RA-B||; M=BA^T
A = points1.T # 2xN
B = points2.T # 2xN
M = np.dot(B, A.T)
U, S, Vt = numpy.linalg.svd(M)
R = np.dot(U, Vt)
'''4 - 构建仿射变换矩阵 '''
s = s2/s1
sR = s*R
c1 = c1.reshape(2,1)
c2 = c2.reshape(2,1)
T = c2 - np.dot(sR,c1) # 模板人脸的中心位置减去 需要对齐的中心位置(经过旋转和缩放之后)
trans_mat = numpy.hstack([sR,T]) # 2x3
return trans_mat
在找到对应的仿射映射矩阵后,可以通过opencv的warpAffine进行映射。
'''上述函数实现的时候,注意模板脸和需要对其的人脸的顺序
landmarks1: 检测出来需要对齐的人脸关键点;
landmarks2:对齐的模板人脸,即平均脸关键点'''
trans_mat = transformation_from_points(landmarks1, landmarks2)
def warp_im(in_image, trans_mat, dst_size):
output_image = cv2.warpAffine(in_image,
trans_mat,
dst_size, # (cols, rows)
borderMode=cv2.BORDER_TRANSPARENT)
return output_image
3 例子
假设当前图片包含4个人脸,如下图,

通过mxnet_mtcnn_face_detection进行检测得到对应的4个人脸边界框和对应的5个关键点

'''边界框[x1, y1, x2, y2, score] '''
[222.22601686, 43.14613463, 280.12375677, 123.65308259, 1. ],
[ 53.22718975, 30.1167623 , 105.30491075, 98.62653339, 0.99999237],
[374.89622349, 44.23550975, 432.30359537, 125.07026242, 0.99998629],
[497.07639685, 32.2071521 , 548.87478065, 105.17269786, 0.99970442]
'''points 关键点[x1, x2 ... x5, y1, y2 ..y5] '''
[255.76176 , 278.4415 , 274.27048 , 255.08255 , 273.5981 , 73.90924 , 75.331924, 92.13313 , 103.375435, 105.174866],
[ 82.20165 , 102.67773 , 99.4637 , 82.03625 , 100.24012 , 55.405067, 55.737637, 69.84144 , 82.090454, 81.33897 ],
[389.51086 , 416.09406 , 397.90732 , 388.24335 , 408.37756 , 68.65562 , 72.8951 , 87.913956, 102.8963 , 105.9071 ],
[513.3108 , 537.25714 , 525.7555 , 514.9328 , 535.16156 , 61.96994 , 61.56072 , 77.64981 , 89.027435, 88.96181 ]
这里修改MTCNN中的对齐代码
def extract_image_chips1( img, points, desired_size=256, padding=0):
"""
crop and align face
Parameters:
----------
img: numpy array, input image
points: numpy array, n x 10 (x1, x2 ... x5, y1, y2 ..y5)
desired_size: default 256
padding: default 0
Retures:
-------
crop_imgs: list, n
cropped and aligned faces
"""
crop_imgs = []
for ind,p in enumerate(points):
# 当前图片中一共有len(points)个人脸
shape =[]
for k in range(len(p)//2):
shape.append(p[k])
shape.append(p[k+5])
if padding > 0:
padding = padding
else:
padding = 0
# 平均脸(模板脸)的5个关键点坐标
mean_face_shape_x = [0.224152, 0.75610125, 0.490127, 0.254149, 0.726104]
mean_face_shape_y = [0.2119465, 0.2119465, 0.628106, 0.780233, 0.780233]
from_points = []
to_points = []
for i in range(len(shape)//2):
x = (padding + mean_face_shape_x[i]) / (2 * padding + 1) * desired_size
y = (padding + mean_face_shape_y[i]) / (2 * padding + 1) * desired_size
to_points.append([x, y])
from_points.append([shape[2*i], shape[2*i+1]])
# 构建人脸关键点矩阵
from_mat = np.asarray(from_points)
to_mat = np.asarray(to_points)
# 计算from_mat映射到to_mat的仿射变换矩阵,是一个2x3的矩阵
trans_mat = transformation_from_points(from_mat,to_mat)
# 进行仿射变换,并取当前中心向外(desired_size,desired_size)大小的区域
dst_size = (desired_size,desired_size)
chips = warp_im(img, trans_mat, dst_size)
crop_imgs.append(chips)
return crop_imgs
chips = extract_image_chips1(img, points, 144, 0.37)
对应的四个旋转矩阵为
array([[ 1.64844171e+00, 8.79546584e-02, -3.74864686e+02],
[-8.79546584e-02, 1.64844171e+00, -4.19148490e+01]])
array([[ 1.84494424e+00, -1.19245336e-02, -9.78834105e+01],
[ 1.19245336e-02, 1.84494424e+00, -4.60283424e+01]])
array([[ 1.48460564e+00, 2.23927075e-01, -5.41851323e+02],
[-2.23927075e-01, 1.48460564e+00, 4.27248780e+01]])
array([[ 1.79634282e+00, -3.48299747e-03, -8.71374899e+02],
[ 3.48299747e-03, 1.79634282e+00, -5.51812653e+01]])
结果如下图所示。




conference: