什么是动态规划（Dynamic Programming）？动态规划的意义是什么？

 

链接：https://www.zhihu.com/question/23995189/answer/613096905
来源：知乎

0. intro

　　很有意思的问题。以往见过许多教材，对动态规划（DP）的引入属于“奉天承运，皇帝诏曰”式：不给出一点引入，见面即拿出一大堆公式吓人；学生则死啃书本，然后突然顿悟。针对入门者的教材不应该是这样的。恰好我给入门者讲过四次DP入门，迭代出了一套比较靠谱的教学方法，所以今天跑过来献丑。

　　现在，我们试着自己来一步步“重新发明”DP。

1. 从一个生活问题谈起

　　先来看看生活中经常遇到的事吧——假设您是个土豪，身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w，需要用到尽量少的钞票。

　　依据生活经验，我们显然可以采取这样的策略：能用100的就尽量用100的，否则尽量用50的……依次类推。在这种策略下，666=6×100+1×50+1×10+1×5+1×1，共使用了10张钞票。

　　这种策略称为“贪心”：假设我们面对的局面是“需要凑出w”，贪心策略会尽快让w变得更小。能让w少100就尽量让它少100，这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明，贪心策略是正确的。

　　但是，如果我们换一组钞票的面值，贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11，那么我们在凑出15的时候，贪心策略会出错：
　　15=1×11+4×1 （贪心策略使用了5张钞票）
　　15=3×5 （正确的策略，只用3张钞票）
　　为什么会这样呢？贪心策略错在了哪里？

　　鼠目寸光。
　　刚刚已经说过，贪心策略的纲领是：“尽量使接下来面对的w更小”。这样，贪心策略在w=15的局面时，会优先使用11来把w降到4；但是在这个问题中，凑出4的代价是很高的，必须使用4×1。如果使用了5，w会降为10，虽然没有4那么小，但是凑出10只需要两张5元。
　　在这里我们发现，贪心是一种只考虑眼前情况的策略。

　　那么，现在我们怎样才能避免鼠目寸光呢？

　　如果直接暴力枚举凑出w的方案，明显复杂度过高。太多种方法可以凑出w了，枚举它们的时间是不可承受的。我们现在来尝试找一下性质。

 

　　重新分析刚刚的例子。w=15时，我们如果取11，接下来就面对w=4的情况；如果取5，则接下来面对w=10的情况。我们发现这些问题都有相同的形式：“给定w，凑出w所用的最少钞票是多少张？”接下来，我们用f(n)来表示“凑出n所需的最少钞票数量”。

　　那么，如果我们取了11，最后的代价（用掉的钞票总数）是多少呢？
　　明显cost=f(4)+1=4+1=5\text{cost} = f(4) + 1 = 4 + 1 = 5 ，它的意义是：利用11来凑出15，付出的代价等于f(4)加上自己这一张钞票。现在我们暂时不管f(4)怎么求出来。
　　依次类推，马上可以知道：如果我们用5来凑出15，cost就是f(10)+1=2+1=3f(10) + 1 = 2 + 1 = 3 。

　　那么，现在w=15的时候，我们该取那种钞票呢？当然是各种方案中，cost值最低的那一个！

　　- 取11：cost=f(4)+1=4+1=5\text{cost}=f(4)+1=4+1=5
　　- 取5： cost=f(10)+1=2+1=3\text{cost}=f(10)+1=2+1=3
　　- 取1： cost=f(14)+1=4+1=5\text{cost}=f(14)+1=4+1=5

　　显而易见，cost值最低的是取5的方案。我们通过上面三个式子，做出了正确的决策！

　　这给了我们一个至关重要的启示—— f(n)f(n) 只与 f(n−1),f(n−5),f(n−11)f(n-1),f(n-5),f(n-11) 相关；更确切地说：

f(n)=\min\{f(n-1),f(n-5),f(n-11)\}+1

　　这个式子是非常激动人心的。我们要求出f(n)，只需要求出几个更小的f值；既然如此，我们从小到大把所有的f(i)求出来不就好了？注意一下边界情况即可。代码如下：

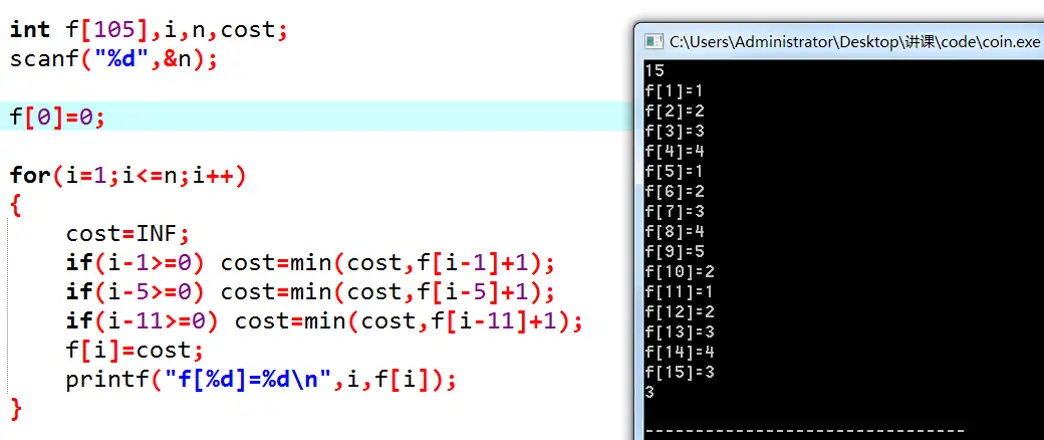
　　我们以 O(n)O(n) 的复杂度解决了这个问题。现在回过头来，我们看看它的原理：

　　- f(n)f(n) 只与f(n−1),f(n−5),f(n−11)f(n-1),f(n-5),f(n-11)的值相关。
　　- 我们只关心 f(w)f(w) 的值，不关心是怎么凑出w的。

　　这两个事实，保证了我们做法的正确性。它比起贪心策略，会分别算出取1、5、11的代价，从而做出一个正确决策，这样就避免掉了“鼠目寸光”！

　　它与暴力的区别在哪里？我们的暴力枚举了“使用的硬币”，然而这属于冗余信息。我们要的是答案，根本不关心这个答案是怎么凑出来的。譬如，要求出f(15)，只需要知道f(14),f(10),f(4)的值。其他信息并不需要。我们舍弃了冗余信息。我们只记录了对解决问题有帮助的信息——f(n).

　　我们能这样干，取决于问题的性质：求出f(n)，只需要知道几个更小的f(c)。我们将求解f(c)称作求解f(n)的“子问题”。

 

　　这就是DP（动态规划，dynamic programming）.

　　将一个问题拆成几个子问题，分别求解这些子问题，即可推断出大问题的解。

思考题：请稍微修改代码，输出我们凑出w的方案。

2. 几个简单的概念

【无后效性】

　　一旦f(n)确定，“我们如何凑出f(n)”就再也用不着了。

　　要求出f(15)，只需要知道f(14),f(10),f(4)的值，而f(14),f(10),f(4)是如何算出来的，对之后的问题没有影响。

　　“未来与过去无关”，这就是无后效性。

　　（严格定义：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。）

 

【最优子结构】

　　回顾我们对f(n)的定义：我们记“凑出n所需的最少钞票数量”为f(n).

　　f(n)的定义就已经蕴含了“最优”。利用w=14,10,4的最优解，我们即可算出w=15的最优解。

　　大问题的最优解可以由小问题的最优解推出，这个性质叫做“最优子结构性质”。

 

　　引入这两个概念之后，我们如何判断一个问题能否使用DP解决呢？

 

　　能将大问题拆成几个小问题，且满足无后效性、最优子结构性质。

 

3. DP的典型应用：DAG最短路

　　问题很简单：给定一个城市的地图，所有的道路都是单行道，而且不会构成环。每条道路都有过路费，问您从S点到T点花费的最少费用。

一张地图。边上的数字表示过路费。

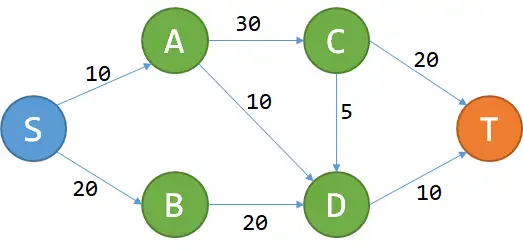
　　这个问题能用DP解决吗？我们先试着记从S到P的最少费用为f(P).
　　想要到T，要么经过C，要么经过D。从而f(T)=min⁡{f(C)+20,f(D)+10}f(T)=\min⁡\{f(C)+20,f(D)+10\}.

　　好像看起来可以DP。现在我们检验刚刚那两个性质：
　　- 无后效性：对于点P，一旦f(P)确定，以后就只关心f(P)的值，不关心怎么去的。
　　- 最优子结构：对于P，我们当然只关心到P的最小费用，即f(P)。如果我们从S走到T是 S→P→Q→TS \to P\to Q\to T ，那肯定S走到Q的最优路径是 S→P→QS\to P\to Q 。对一条最优的路径而言，从S走到沿途上所有的点（子问题）的最优路径，都是这条大路的一部分。这个问题的最优子结构性质是显然的。

　　既然这两个性质都满足，那么本题可以DP。式子明显为：

f(P)=\min⁡\{f(R)+w_{R→P}\}

　　其中R为有路通到P的所有的点， wR→Pw_{R→P} 为R到P的过路费。

　　代码实现也很简单，拓扑排序即可。

4. 对DP原理的一点讨论

【DP的核心思想】

• 　　DP为什么会快？

　　无论是DP还是暴力，我们的算法都是在可能解空间内，寻找最优解。

　　来看钞票问题。暴力做法是枚举所有的可能解，这是最大的可能解空间。
　　DP是枚举有希望成为答案的解。这个空间比暴力的小得多。

　　也就是说：DP自带剪枝。

　　DP舍弃了一大堆不可能成为最优解的答案。譬如：
　　15 = 5+5+5 被考虑了。
　　15 = 5+5+1+1+1+1+1 从来没有考虑过，因为这不可能成为最优解。

　　从而我们可以得到DP的核心思想：尽量缩小可能解空间。

　　在暴力算法中，可能解空间往往是指数级的大小；如果我们采用DP，那么有可能把解空间的大小降到多项式级。

　　一般来说，解空间越小，寻找解就越快。这样就完成了优化。

 

【DP的操作过程】

　　一言以蔽之：大事化小，小事化了。

　　将一个大问题转化成几个小问题；
　　求解小问题；
　　推出大问题的解。

【如何设计DP算法】

　　下面介绍比较通用的设计DP算法的步骤。

• 　　首先，把我们面对的局面表示为x。这一步称为设计状态。
• 　　对于状态x，记我们要求出的答案(e.g. 最小费用)为f(x).我们的目标是求出f(T).
• 找出f(x)与哪些局面有关（记为p），写出一个式子（称为状态转移方程），通过f(p)来推出f(x).

【DP三连】

　　设计DP算法，往往可以遵循DP三连：

• 　　我是谁？ ——设计状态，表示局面
• 　　我从哪里来？
• 　　我要到哪里去？ ——设计转移

　　设计状态是DP的基础。接下来的设计转移，有两种方式：

• 一种是考虑我从哪里来（本文之前提到的两个例子，都是在考虑“我从哪里来”）；
• 另一种是考虑我到哪里去，这常见于求出f(x)之后，更新能从x走到的一些解。这种DP也是不少的，我们以后会遇到。

　　总而言之，“我从哪里来”和“我要到哪里去”只需要考虑清楚其中一个，就能设计出状态转移方程，从而写代码求解问题。前者又称pull型的转移，后者又称push型的转移。（这两个词是

@阮止雨

妹妹告诉我的，不知道源出处在哪）

 

思考题：如何把钞票问题的代码改写成“我到哪里去”的形式？
提示：求出f(x)之后，更新f(x+1),f(x+5),f(x+11).

5. 例题：最长上升子序列

　　扯了这么多形而上的内容，还是做一道例题吧。

　　最长上升子序列（LIS）问题：给定长度为n的序列a，从a中抽取出一个子序列，这个子序列需要单调递增。问最长的上升子序列（LIS）的长度。
　　e.g. 1,5,3,4,6,9,7,8的LIS为1,3,4,6,7,8，长度为6。

 

　　如何设计状态（我是谁）？

　　我们记 f(x)f(x) 为以 axa_x 结尾的LIS长度，那么答案就是 max{f(x)}\max\{f(x)\} .

 

　　状态x从哪里推过来（我从哪里来）？

　　考虑比x小的每一个p：如果 ax>apa_x>a_p ，那么f(x)可以取f(p)+1.
　　解释：我们把 axa_x 接在 apa_p 的后面，肯定能构造一个以 axa_x 结尾的上升子序列，长度比以 apa_p 结尾的LIS大1.那么，我们可以写出状态转移方程了：

f(x)=\max_{p<x , a_p<a_x }⁡\{f(p)\}+1

　　至此解决问题。两层for循环，复杂度 O(n2)O(n^2) .

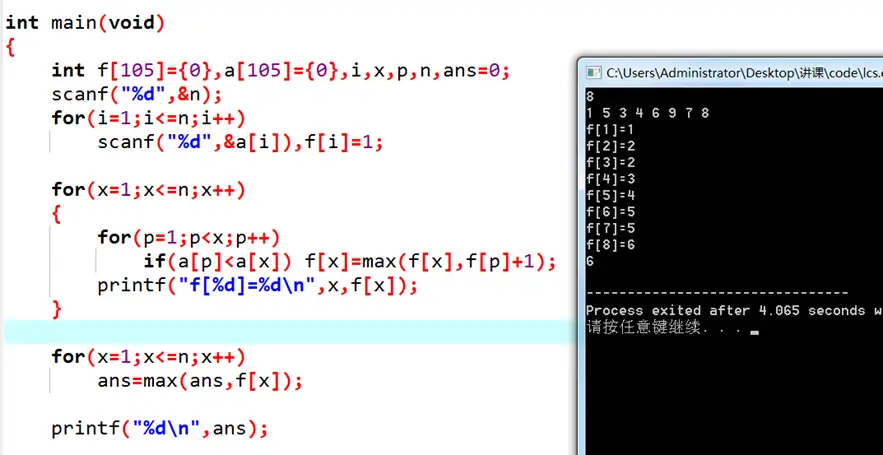
　　从这三个例题中可以看出，DP是一种思想，一种“大事化小，小事化了”的思想。带着这种思想，DP将会成为我们解决问题的利器。

　　最后，我们一起念一遍DP三连吧——我是谁？我从哪里来？我要到哪里去？

6. 习题

如果读者有兴趣，可以试着完成下面几个习题：

一、请采取一些优化手段，以 O(nlog⁡n)O(n\log n) 的复杂度解决LIS问题。

提示：可以参考这篇博客 Junior Dynamic Programming--动态规划初步·各种子序列问题

二、“按顺序递推”和“记忆化搜索”是实现DP的两种方式。请查阅资料，简单描述“记忆化搜索”是什么。并采用记忆化搜索写出钞票问题的代码，然后完成P1541 乌龟棋 - 洛谷 。

三、01背包问题是一种常见的DP模型。请完成P1048 采药 - 洛谷。

 

谢谢您看完本文 ⁄(⁄ ⁄ ⁄ω⁄ ⁄ ⁄)⁄