论文阅读 | DynaBERT: Dynamic BERT with Adaptive Width and Depth
DynaBERT: Dynamic BERT with Adaptive Width and Depth
论文中作者提出了新的训练算法，同时对不同尺寸的子网络进行训练，通过该方法训练后可以在推理阶段直接对模型裁剪。依靠新的训练算法，本文在效果上超越了众多压缩模型，比如DistillBERT、TinyBERT以及LayerDrop后的模型。
论文对于BERT的压缩流程是这样的：
- 训练时，对宽度和深度进行裁剪，训练不同的子网络
- 推理时，根据速度需要直接裁剪，用裁剪后的子网络进行预测
整体的训练分为两个阶段，先进行宽度自适应训练，再进行宽度+深度自适应训练。
宽度自适应 Adaptive Width
宽度自适应的训练流程是：
- 得到适合裁剪的teacher模型，并用它初始化student模型
- 裁剪得到不同尺寸的子网络作为student模型，对teacher进行蒸馏
在MHA中，我们认为不同的head抽取到了不同的特征，因此每个head的作用和权重肯定也是不同的，intermediate中的神经元连接也是。如果直接按照粗暴裁剪的话，大概率会丢失重要的信息，因此作者想到了一种方法，对head和神经元进行排序，每次剪枝掉不重要的部分，并称这种方法为Netword Rewiring。重要程度的计算核心思想是计算去掉head之前和之后的loss变化，变化越大则越重要。[Analyzing multi-head self-attention]
利用Rewiring机制，便可以对注意力头和神经元进行排序，得到第一步的teacher模型，如图：
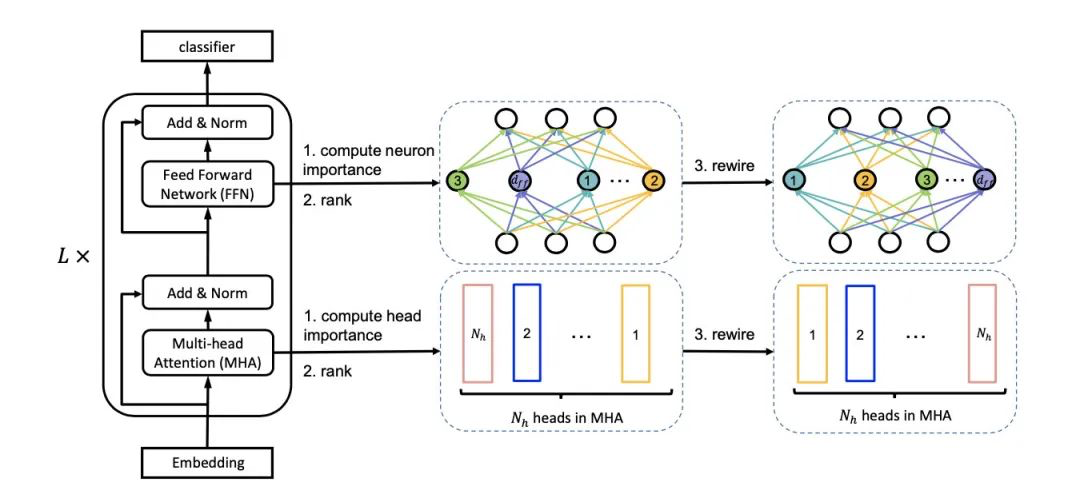
要注意的是，虽然随着参数更新，注意力头和神经元的权重会变化，但teacher模型只初始化一次（在后文有验证增加频率并没带来太大提升）。之后，每个batch会训练mw=[1.0, 0.75, 0.5, 0.25]四种student模型，如图：
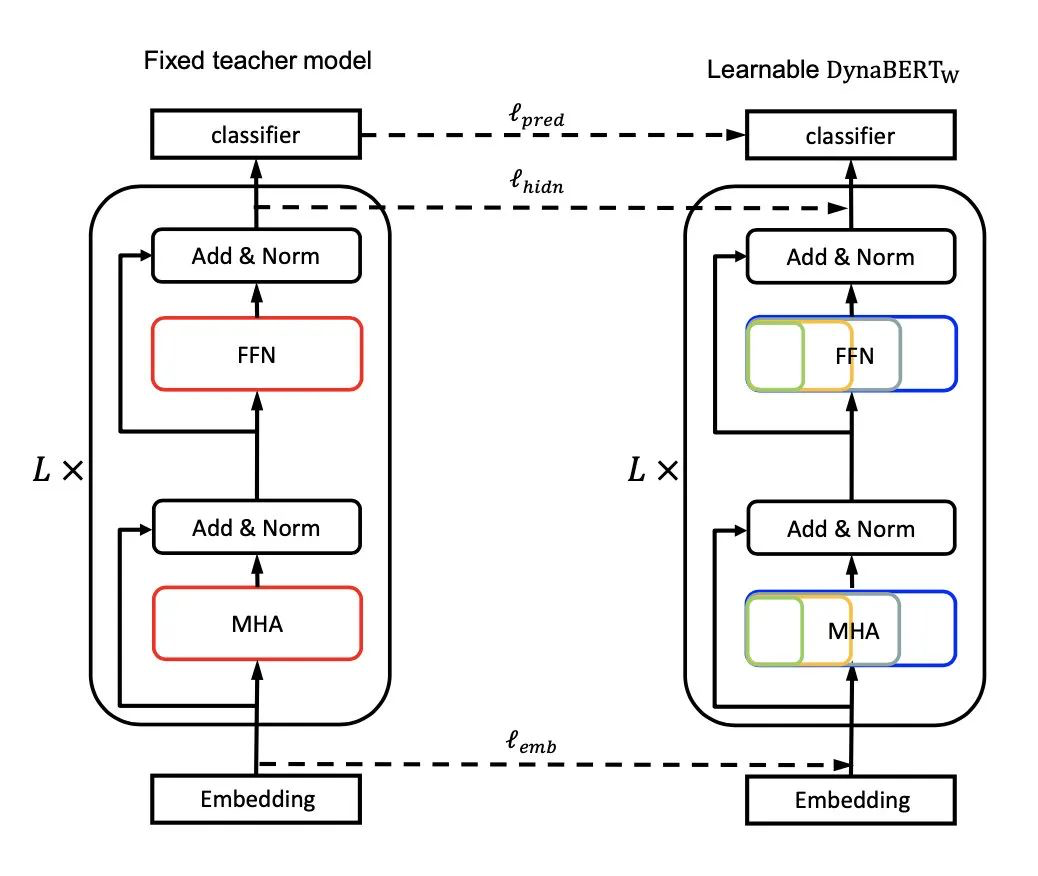
蒸馏的最终loss来源于三方面：logits、embedding和每层的hidden state。
(soft cross-entropy loss)
（computed over all L Transformer layers）
最终的loss公式：
论文中取(lambda1, lambda2) = (1, 0.1)
emb和hidden的loss权重是因为他们有相同的维度和相似的规模。
深度自适应 Adaptive Depth
训好了width-adaptive的模型之后，就可以训自适应深度的了。浅层BERT模型的优化其实比较成熟了，主要的技巧就是蒸馏。作者直接使用训好的DynaBERTw作为teacher，蒸馏裁剪深度后的小版本BERT。
对于深度，系数md = [1.0, 0,75, 0,5]，设层的深度为[1,12]，作者根据mod(d+1, 1/md) ≡ 0去掉深度为d的层。之所以取d+1是因为研究表明最后一层比较重要[Minilm]。
例如，对于BERT，包含12个transformer层1,2,...,12，当md=0.75时，被drop的层是深度为3，7，11的。（因为用了d+1，所以第12层没有被drop）
最终被保留的层的loss：
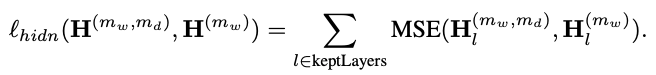
整体loss：
最后，为了避免灾难性遗忘，作者继续对宽度进行剪枝训练，第二阶段的训练方式如图：
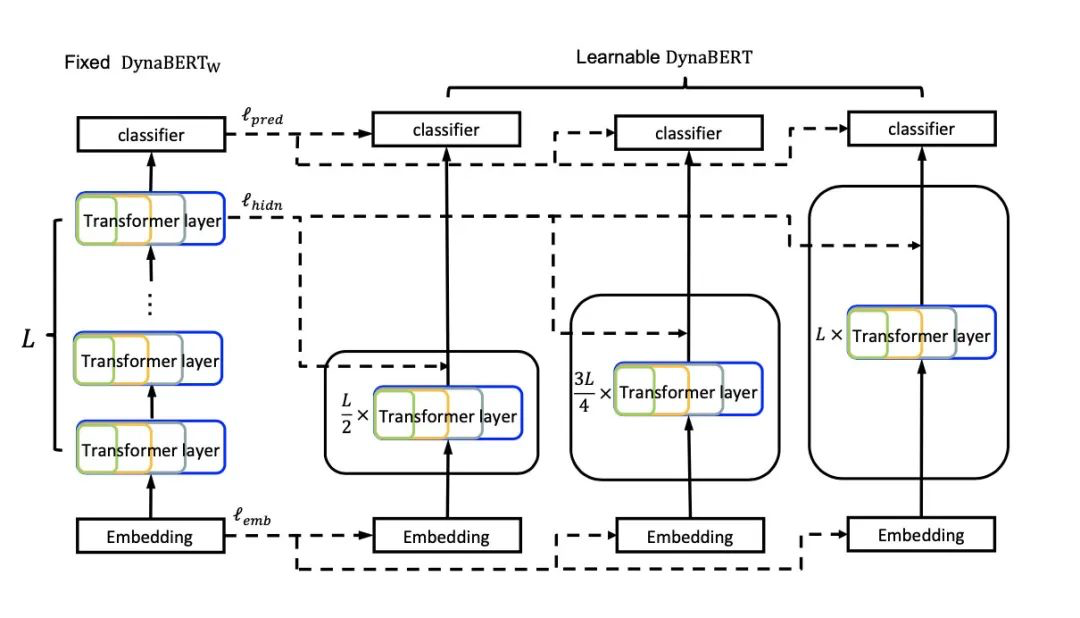
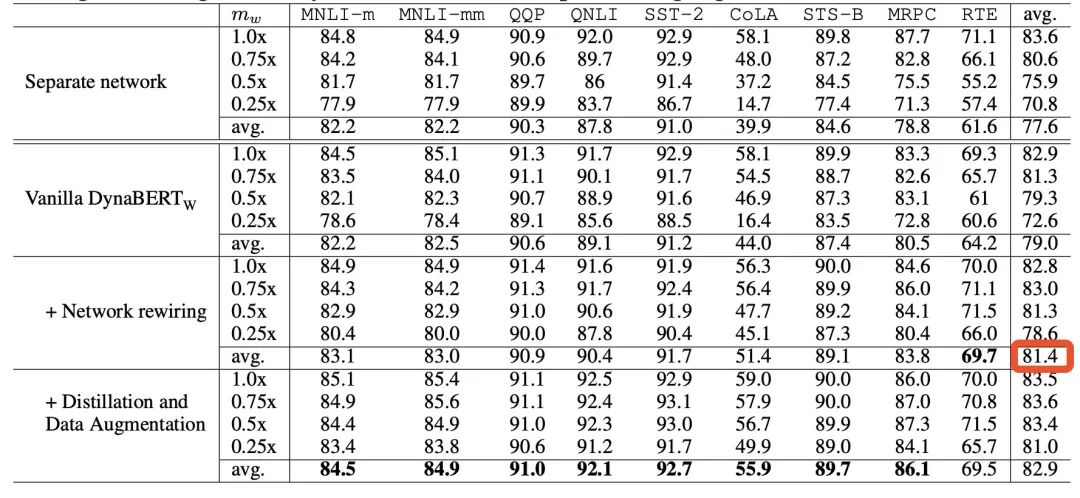
根据训练时宽度和深度的裁剪系数，作者最终可得到12个大小不同的BERT模型，在GLUE上的效果如下：
可以看到，剪枝的BERT效果并没有太多下降，并且在9个任务中都超越了BERT-base。同时，这种灵活的训练方式也给BERT本身的效果带来了提升，在与BERT和RoBERTa的对比中都更胜一筹：
另外，作者还和DistillBERT、TinyBERT、LayerDrop进行了实验对比，DynaBERT均获得了更好的效果。
在消融实验中，作者发现在加了rewiring机制后准确率平均提升了2个点之多：
结论
本篇论文的创新点主要在于Adaptive width的训练方式，考虑到后续的裁剪，作者对head和neuron进行了排序，并利用蒸馏让子网络学习大网络的知识。
总体来说还是有些点可以挖的，比如作者为什么选择先对宽度进行自适应，再宽度+深度自适应？这样的好处可能是在第二阶段的蒸馏中学习到宽度自适应过的子网络知识。但直接进行同时训练不可以吗？还是希望作者再验证一下不同顺序的差距。
为了简化，作者在宽度上所做的压缩比较简单，之后可以继续尝试压缩hidden dim。另外，ALBERT相比原始BERT其实更适合浅层Transformer，也可以作为之后的尝试方向。
参考：
别再蒸馏3层BERT了！变矮又能变瘦的DynaBERT了解一下
