堆排序
特点:
1. 与合并排序类似,运行时间$O(nlgn)$,比插入排序快
2. 与插入排序类似,堆排序为in-place排序算法,空间复杂度$O(1)$,在任何时候,数组只有常熟个元素存储在输入数组以外。
最大堆如图所示:
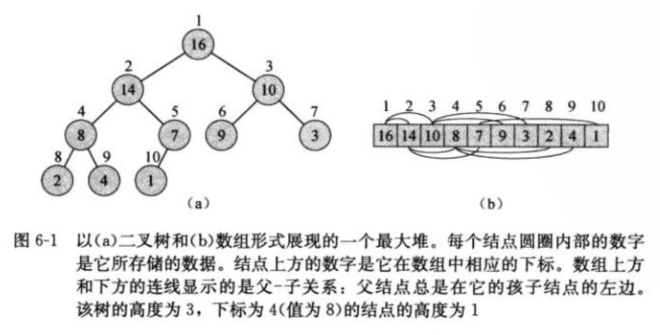
堆可以用数组来进行实现。树的根为A[1] ,给定了某个节点i ,其父节点 parent(i) ,左子节点 left(i) 和右子节点 right(i) 在数组中的下标可以简单计算如下:
用0作为数组起始下标,python实现如下所示
def left(i): return 2 * (i + 1) - 1 def right(i): return 2 * (i + 1) def parent(): return (i + 1) * 2 - 1
二叉堆有两种,最大堆和最小堆。最大堆是指父节点比子节点大,最大元素存放在根节点,并且在以一个节点为根的子树中,各节点的值都不大于该子树根节点的值。
最小堆恰好相反:
以最大堆为例:保持堆的性质
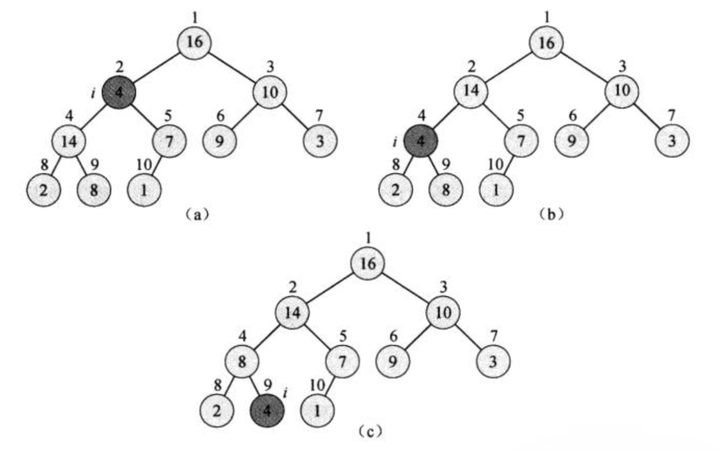
例如下图中,对 $A[2]$ 进行check, $max{ 4, 14, 7} = 7$,因此$A[2]$ ,$A[4]$ 进行switch,然后沿着$A[4]$的子节点进行递归, $max{4,2,8}=8$,然后再进行switch,直到碰到叶子节点。
在检查的时候只需要switch $A[i], A[largest]$,然后沿着被switch的节点(位置为largest的节点)为根的子树进行递归检查,另一个子树不需要检查。
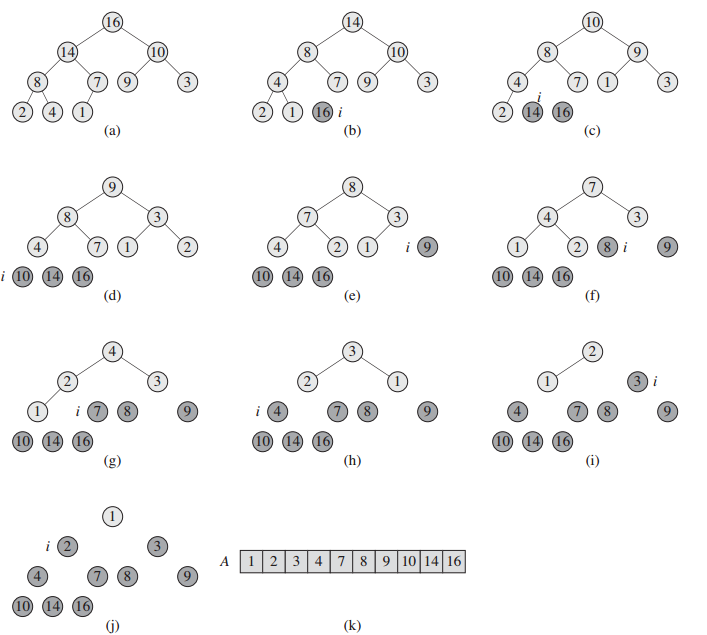
建堆
首先给出一个问题并进行证明:当用数组表示存储了n个元素的堆时,叶子节点的下标是

给定一个不明顺序的数组表示的堆,如何构造最大堆?
def build_max_head(A): i = len(A) / 2 - 1 while i >= 0: max_heapify(A, i) i -= 1 if __name__ == '__main__': A=[1,2,3,4,5] build_max_head(A) print A 输出结果为: [5, 4, 3, 1, 2]
如上所述,对所有的非叶子节点,自下往上地调用MAX-HEAPIFY,始终维持着子树的最大堆属性,因此到根节点,整个树就成为最大堆。
构建堆的时间复杂度为$O(n)$。
堆排序算法HEAP-SORT
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
def head_sort(A): result = [] build_max_head(A) while len(A) > 1: result.append(A[0]) A[0],A[len(A)-1] = A[len(A)-1],A[0] A = A[:-1] max_heapify(A,0) result.extend(A) return result if __name__ == '__main__': A=[1,2,3,4,5,7,8,10,400] result = head_sort(A) print result 输出结果为: [400, 10, 8, 7, 5, 4, 3, 2, 1]
算法步骤如下:
- 首先对数组进行建堆,这样得到最大堆
- 取堆的根节点,也就是最大值
- 保持树的结构不变,将根节点与最后一个值交换,然后对根节点进行MAX-HEAPIFY,这样第二大的值就成为根节点,因此类推
这里需要注意两点:
- 实现的时候才用了额外的list来存放,也可以采用额外的变量heap-size来进行处理,每次只处理
范围的数据,这样就是完全的in-place了
- 循环过程中,每次都将
进行交换,这样就不会修改树的结构,然后直接进行MAX-HEAPIFY
完整示例
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
假设给定无序序列结构如下

此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 [数组长度/2]=[5/2]=1,也就是下面的6结点 []为向下取整),从左至右,从下至上进行调整。

第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。

这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。

此时,我们就将一个无需序列构造成了一个大顶堆。
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
a.将堆顶元素9和末尾元素4进行交换

b.重新调整结构,使其继续满足堆定义

c.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.

后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序

再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
完整代码 C++
void buildMaxHeap(int A[], int n) //建立最大堆 { // 从最后一个非叶子节点(n/2-1)开始自底向上构建, for (int i = n / 2-1; i >= 0; i--) //从(n/2-1)调用一次maxHeapIfy就可以得到最大堆 maxHeapIfy(A, i, n); } void maxHeapIfy(int A[], int i, int n) //将i节点为根的堆中小的数依次上移,n表示堆中的数据个数 { int l = 2 * i + 1; //i的左儿子 int r = 2 * i + 2; //i的右儿子 int largest = i; //先设置父节点和子节点三个节点中最大值的位置为父节点下标 if (l < n && A[l] > A[largest]) largest = l; if (r < n && A[r] > A[largest]) largest = r; if (largest != i) //最大值不是父节点,交换 { swap(A[i],A[largest]); maxHeapIfy(A, largest, n); //递归调用,保证子树也是最大堆 } } void heapSort(int A[], int n) //堆排序算法 { buildMaxHeap(A, n); //先建立堆 for (int i = n-1; i >0; i--) { // 将根节点(最大值)与数组待排序部分的最后一个元素交换,这样最终得到的是递增序列 swap(A[0], A[i]); // 待排序数组长度减一,只要对换到根节点的元素进行排序,将它下沉就好了。 maxHeapIfy(A, 0, i); } }
堆排序是一种选择排序,整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆复杂度为$O(n)$,在交换并重建堆的过程中,需交换n-1次,而重建堆的过程中,根据完全二叉树的性质,[log2(n-1),log2(n-2)...1]逐步递减,近似为$nlogn$。所以堆排序时间复杂度一般认为就是$O(nlogn)$级。

