理解KMP算法
由暴力匹配引入KMP算法 ---->
暴力匹配算法
问题:有一个文本串S,和一个模式串P,现在要查找P在S中的位置。
如果用暴力匹配的思路,并假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置,则有:
- 如果当前字符匹配成功(即S[i] == P[j]),则i++,j++,继续匹配下一个字符;
- 如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯,j 被置为0。(之前已经匹配好的j-1个字符串全推翻)
示例:(上面S, 下面P)
比如从A这里开始匹配上了:

一直这样匹配下去:

到这里匹配不上了:

就回滚回去重新开始:

这种回滚的问题在于:
在之前第4步匹配中,我们已经得知S[5] = P[1] = B,而P[0] = A,即P[1] != P[0],故S[5]必定不等于P[0],所以回溯过去必然会导致失配。
就是说,图上S中红框B我们之前就知道不等于下面这个红框A了,回溯回去也没用。
那有没有一种算法,让i 不往回退,只需要移动j 即可呢?
YES ===> KMP算法,它利用之前已经部分匹配这个有效信息,保持i 不回溯,通过修改j 的位置,让模式串尽量地移动到有效的位置。
KMP算法
Knuth-Morris-Pratt 字符串查找算法,简称为 “KMP 算法”,常用于在一个文本串 S 内查找一个模式串 P 的出现位置,这个算法由 Donald Knuth、Vaughan Pratt、James H. Morris 三人于 1977 年联合发表,故取这三人的姓氏命名此算法。
下面先直接给出 KMP 的算法流程(后续会详述):
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置:
- 如果next[j] = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
- 如果next[j] != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。(不像上面的暴力匹配要移动i)
示例:
接着看上面的例子,到这里发现匹配不到:
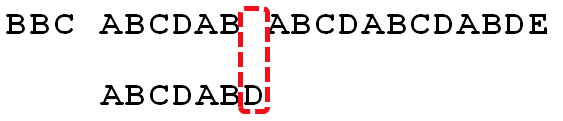
然后我们回退到这里(i没有变,j向右移动4位 ==> 为什么要向右移动4位呢,因为移动4位后,模式串中又有个“AB”可以继续跟S[8]S[9]对应着,从而不用让i 回溯):KMP算法的思想是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
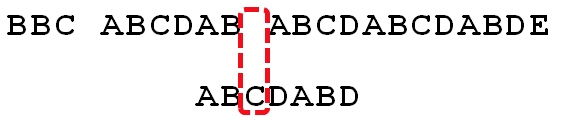
可以看到,失配时,模式串向右移动的位数为:已匹配字符数 - 失配字符的上一位字符所对应的最大长度值
完整的例子:
如果给定文本串“BBC ABCDAB ABCDABCDABDE”,和模式串“ABCDABD”,现在要拿模式串去跟文本串匹配。
移动位数 = 已匹配的字符数 - 对应的部分匹配值 ==> 最大长度表 / NEXT数组
原模式串子串对应的各个前缀后缀的公共元素的最大长度表/next 数组为:
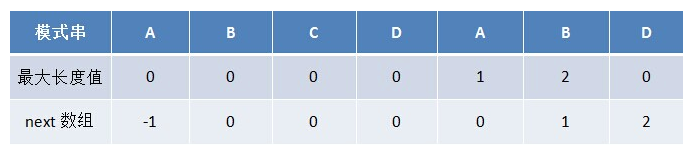
我们看下上表是如何构造的:
最大长度值(也称"部分匹配值")就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
再copy一遍上面的算法流程:
- 如果next[j] = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
- 如果next[j] != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。(不像上面的暴力匹配要移动i)
示例匹配过程如下:

1. 因为模式串中的字符A跟文本串中的字符B、B、C、空格一开始就不匹配,直接将模式串不断的右移一位即可,直到模式串中的字符A跟文本串的第5个字符A匹配成功:

2. 继续往后匹配,当模式串最后一个字符D跟文本串匹配时失配,模式串需要向右移动。但向右移动多少位呢?因为此时已经匹配的字符数为6个(ABCDAB),然后根据《最大长度表》可得失配字符D的上一位字符B对应的长度值为2,所以根据之前的结论,可知需要向右移动6 - 2 = 4 位。
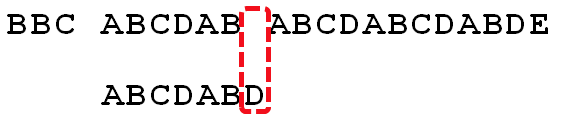
3. 模式串向右移动4位后,发现C处再度失配,因为此时已经匹配了2个字符(AB),且上一位字符B对应的最大长度值为0,所以向右移动:2 - 0 =2 位。

4. A与空格失配,向右移动1 位。

5. 继续比较,发现D与C 失配,故向右移动的位数为:已匹配的字符数6减去上一位字符B对应的最大长度2,即向右移动6 - 2 = 4 位。

6. 经历第5步后(匹配CDABD的部分),发现匹配成功,过程结束。

通过上述匹配过程可以看出,问题的关键就是寻找模式串中最大长度的相同前缀和后缀,基于此匹配。
关键:求解Next数组 ==> 可以参考下面的[参考 4]。

