模型融合
结合/融合/整合 (integration/ combination/ fusion)多个机器学习模型往往可以提高整体的预测能力。这是一种非常有效的提升手段,在多分类器系统(multi-classifier system)和集成学习(ensemble learning)中,融合都是最重要的一个步骤。
举个实用的例子,Kaggle比赛中常用的stacking方法就是模型融合,通过结合多个各有所长的子学习器,我们实现了更好的预测结果。基本的理论假设是:不同的子模型在不同的数据上有不同的表达能力,我们可以结合他们擅长的部分,得到一个在各个方面都很“准确”的模型。当然,最基本的假设是子模型的误差是互相独立的,这个一般是不现实的。但即使子模型间的误差有相关性,适当的结合方法依然可以各取其长,从而达到提升效果。
相关方法
平均法/投票法
比较简单,不做赘述。采用平均法的另一个风险在于可能被极值所影响。正态分布的取值是 ,在少数情况下平均值会受到少数极值的影响。一个常见的解决方法是,用中位数(median)来代替平均数进行整合。另一个问题是子模型良莠不齐。如果10个模型中有1个表现非常差,那么会拖累最终的效果,适得其反。因此,简单、粗暴的把所有子模型通过平均法整合起来效果往往一般。
赋予不同子模型不同的权重
给优秀的子模型更大的权重。在这种前提下,一个比较直白的方法就是根据子模型的准确率给出一个参考权重 ,子模型越准确那么它的权重就更大,对于最终预测的影响就更强:
。简单取平均是这个方法的一个特例,即假设子模型准确率一致。
学习分类器权重
这是Stacking的核心思路。通过增加一层来学习子模型的权重。
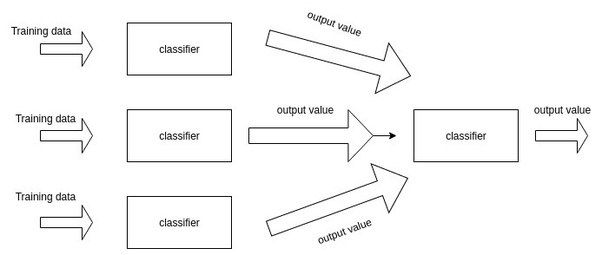
更多有关于stacking的讨论可以参考我:「Stacking」与「神经网络」。简单来说,就是加一层逻辑回归或者SVM,把子模型的输出结果当做训练数据,来自动赋予不同子模型不同的权重。
一般来看,这种方法只要使用得当,效果应该比简单取平均值、或者根据准确度计算权重的效果会更好。
挖掘局部关系
上面提到的方法,都有一个不可避免的问题,那就是对于问题处理是全局的(global)。一个分类器不一定在每个局部上表现都好,而我们赋予的全局权重会无差别的认为:”一个子模型在全局的表现上一致“,这是不现实的。
因此,另一个非常有效的融合方法就是:动态分类器选择(Dynamic Classifier Selection),简称DCS。DCS的思路是,当我们遇到一个新的数据需要去预测时,我们首先找到训练数据中和新数据临近的k个数据,一般这个搜寻可以通过k-近邻来实现。找到以后,我们只需要找到在k个相邻的训练数据构成的局部空间上,选择表现最好的分类器。它可能是逻辑回归,也可能是SVM,但思路是找到最好的那一个即可。
这种做法的最大优点是考虑到了不同分类器在不同局部的表现能力可能有差异,不该默认分类器的全局表现一样。在这个基础上,研究人员还提出 动态集成选择(Dynamic Ensemble Selection),DES的区别在于目标是找到局部上表现较好的几个子模型来共同预测,可以理解为集成上的集成。
当然,天下没有免费的午餐,使用DCS和DES的最大弊端就是运算开销。与简单的平均相比,这种繁复的方法有很高的时间复杂度。
神经网络与Stacking
Stacking是Kaggle比赛中常见的集成学习框架。一般来说,就是训练一个多层(一般是两层,本文中默认两层)的学习器结构,第一层(也叫学习层)用n个不同的分类器(或者参数不同的模型)将得到预测结果合并为新的特征集,并作为下一层分类器的输入。通过第二层的输出训练器得到了最终预测结果。
stacking中一般都用交叉验证来避免过拟合。
为了降低过拟合的问题,第二层分类器应该是较为简单的分类器,广义线性如逻辑回归是一个不错的选择。在特征提取的过程中,我们已经使用了复杂的非线性变换,因此在输出层不需要复杂的分类器。这一点可以对比神经网络的激活函数或者输出层,都是很简单的函数,一点原因就是不需要复杂函数并能控制复杂度。
因此,stacking的输出层不需要过分复杂的函数,用逻辑回归还有额外的好处:
- 配合L1正则化还可以进一步防止过拟合
- 配合L1正则化还可以选择有效特征,从第一层的学习器中删除不必要的分类器,节省运算开销。
- 逻辑回归的输出结果还可被理解为概率
一般来看,2层对于stacking足够了。多层的stacking会面临更加复杂的过拟合问题,且收益有限。
stacking与深度学习不同之处:
- stacking需要宽度,深度学习不需要
- 深度学习需要深度,而stacking不需要
stacking和深度学习都共同需要面临:
- 黑箱与解释问题
- 严重的过拟合问题
相关文献:
Džeroski, S. and Ženko, B., 2004. Is combining classifiers with stacking better than selecting the best one?. Machine learning, 54(3), pp.255-273.
