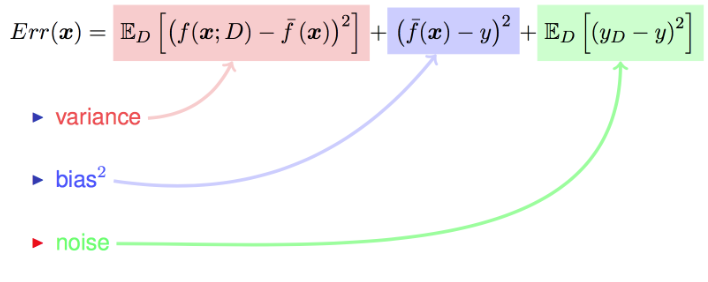
高/低方差、高/低偏差
概念
偏差: 描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据集。
(假设靶心是最适合给定数据的模型,离靶心越远,我们的预测就越糟糕)
方差: 描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,预测结果数据的分布越散。

基于偏差的误差: 模型预期的预测与我们将要预测的真实值之间的差值。偏差是用来衡量模型的预测同真实值的差异。
基于方差的误差: 模型对给定的数据进行预测的可变性。比如,当你多次重复构建完整模型的进程时,方差是,在预测模型的不同关系间变化的多少。
对上图的解释:
左上:低偏差,低方差。表现出来就是,预测结果准确率很高,并且模型比较健壮(稳定),预测结果高度集中。
右上:低偏差,高方差。表现出来就是,预测结果准确率较高,并且模型不稳定,预测结果比较发散。
左下:高偏差,低方差。表现出来就是,预测结果准确率较低,但是模型稳定,预测结果比较集中。
右下:高偏差,高方差。表现出来就是,预测结果准确率较低,模型也不稳定,预测结果比较发散。
举个例子
想象你开着一架黑鹰直升机,得到命令攻击地面上一只敌军部队,于是你连打数十梭子,结果有一下几种情况:
1.子弹基本上都打在队伍经过的一棵树上了,连在那棵树旁边等兔子的人都毫发无损,这就是方差小(子弹打得很集中),偏差大(跟目的相距甚远)。
2.子弹打在了树上,石头上,树旁边等兔子的人身上,花花草草也都中弹,但是敌军安然无恙,这就是方差大(子弹到处都是),偏差大(跟目的相距甚远)。
3.子弹打死了一部分敌军,但是也打偏了些打到花花草草了,这就是方差大(子弹不集中),偏差小(已经在目标周围了)。
4.子弹一颗没浪费,每一颗都打死一个敌军,跟抗战剧里的八路军一样,这就是方差小(子弹全部都集中在一个位置),偏差小(子弹集中的位置正是它应该射向的位置)。
方差,是形容数据分散程度的,算是“无监督的”,客观的指标,偏差,形容数据跟我们期望的中心差得有多远,算是“有监督的”,有人的知识参与的指标。
IF YOU NEED MORE
偏差(bias):对象是单个模型, 期望输出与真实标记的差别。
方差(Variance):对象是多个模型,表示多个模型差异程度。
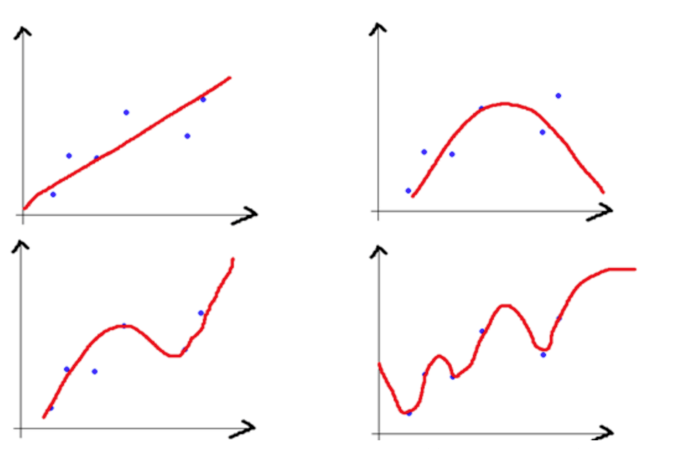
以上图为例:
1. 左上的模型偏差最大,右下的模型偏差最小;
2. 左上的模型方差最小,右下的模型方差最大。
为了理解第二点,可以看下图。蓝色和绿色分别是同一个训练集上采样得到的两个训练子集,由于采取了复杂的算法去拟合,两个模型差异很大(===> 导致方差大)。如果是拿直线拟合的话,显然差异不会这么大。

一般来说,偏差、方差和模型的复杂度之间的关系如下图所示:
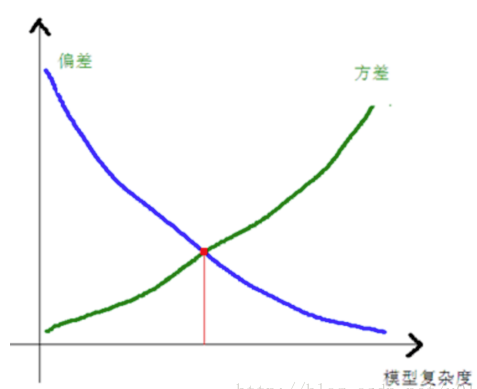
越复杂的模型偏差越小,而方差越大。
我们用一个参数少的,简单的模型进行预测,会得到低方差,高偏差,通常会出现欠拟合。
而我们用一个参数多的,复杂的模型进行预测,会得到高方差,低偏差,通常出现过拟合。
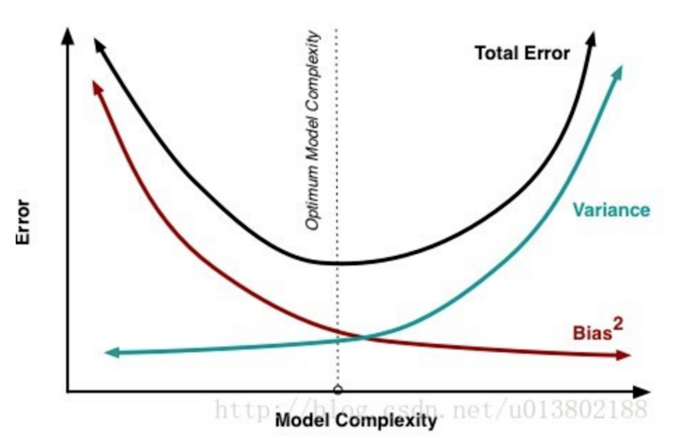
其中:
$\frac{d_{Bias}}{d_{Complexity}} = -\frac{d_{Variance}}{d_{Complexity}} $
实际中,我们需要找到偏差和方差都较小的点。从上图可以看出在偏差和方差都较小的点处,total Error是最少的。
XGBOOST中,我们选择尽可能多的树,尽可能深的层,来减少模型的偏差;
通过cross-validation,通过在验证集上校验,通过正则化,来减少模型的方差从而获得较低的泛化误差。
拓展
数学上的定义:
定义要预测的变量为$Y$,协变量为$X$,假设有$Y=f(X)+ϵ$,其中误差项服从均值为0的正态分布。
我们用线性回归或者别的模型来估计$f(X)$ 为$\hat{f}(X)$。其中,对x来说,误差为:
$Err(x) = E[(Y-\hat{f}(x))^{2}]$
将上式展开,然后用偏差和方差表述:
$Err(x) = (E[\hat{f}(x)]-f(x))^{2} + E[\hat{f}(x)-E[\hat{f}(x)]]^{2} + \sigma ^{2}$
$Err(x) = Bias^{2} + Variance + Irreducible Error$
注意:最后一项为噪声,是无法通过模型降低的。
通过上面的式子也可看出,要使得误差低,就要使得偏差和方差都要低。
* 公式分解过程:
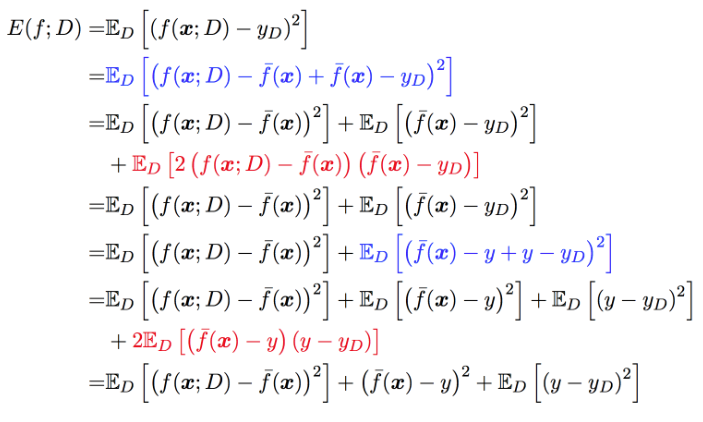
红色部分=0:
第一部分:
$E_{D}[2(f(x; D) -\bar{f}(x))(\bar{f}(x)-y_{D})]^{2}$
$=2E_{D}[f(x; D)\bar{f}(x)- f(x; D)y_{D}-\bar{f}(x)^{2}+\bar{f}(x)y_{D}]$
其中:
$E_{D}[f(x; D)\bar{f}(x)] = \bar{f}(x)^{2}$
$E_{D}[y_{D}f(x; D)] = y_{D}\bar{f}(x)$
第二部分:
基于噪声期望为0的假设:
$E_{D}[y - y_{D}] = 0 $