Layer Normalization, Instance Normalization, Group Normalization
1 Layer Normalization
为了能够在只有当前一个训练实例的情形下,也能找到一个合理的统计范围,一个最直接的想法是:MLP的同一隐层自己包含了若干神经元;同理,CNN中同一个卷积层包含k个输出通道,每个通道包含m*n个神经元,整个通道包含了k*m*n个神经元;类似的,RNN的每个时间步的隐层也包含了若干神经元。那么我们完全可以直接用同层隐层神经元的响应值作为集合S的范围来求均值和方差。这就是Layer Normalization的基本思想。图1、图2和图3分示了MLP、CNN和RNN的Layer Normalization的集合S计算范围。

图1. MLP中的LayerNorm
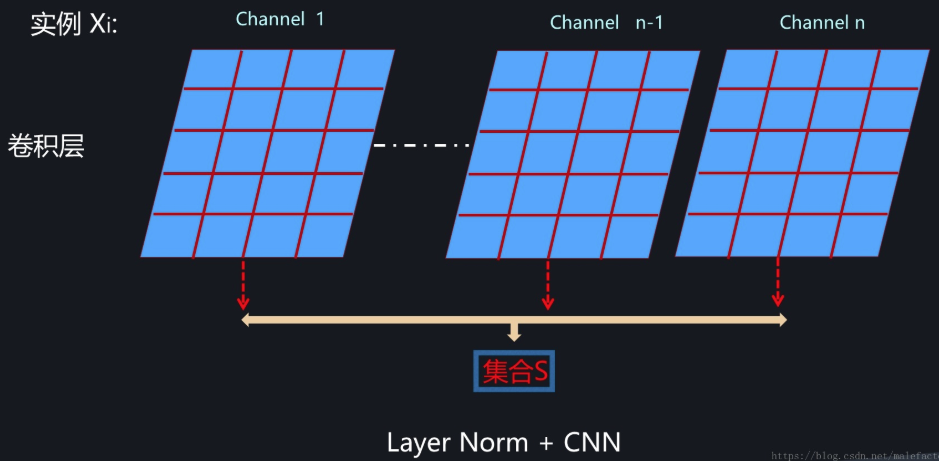
图2. CNN中的LayerNorm
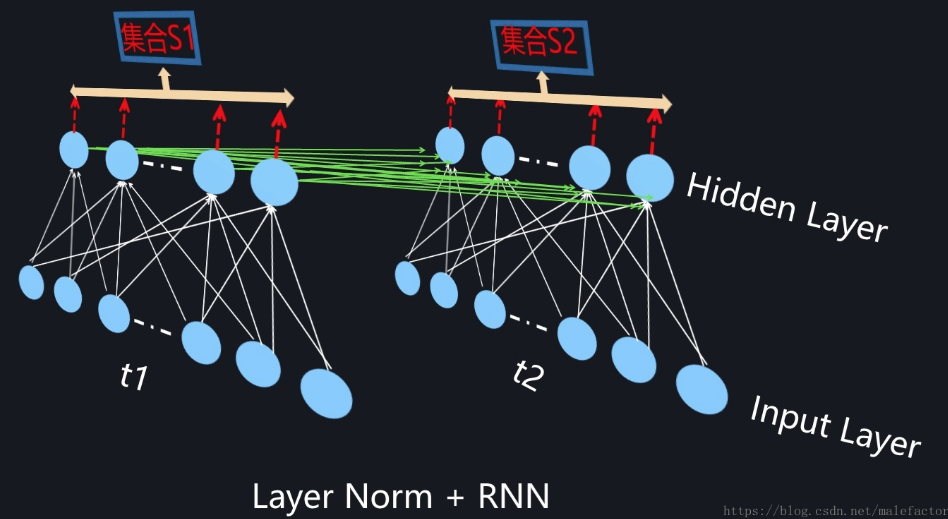
图3. RNN中的LayerNorm
前文有述,BN在RNN中用起来很不方便,而Layer Normalization这种在同隐层内计算统计量的模式就比较符合RNN这种动态网络,目前在RNN中貌似也只有LayerNorm相对有效,但Layer Normalization目前看好像也只适合应用在RNN场景下,在CNN等环境下效果是不如BatchNorm或者GroupNorm等模型的。从目前现状看,动态网络中的Normalization机制是非常值得深入研究的一个领域。
2 Instance Normalization
从上述内容可以看出,Layer Normalization在抛开对Mini-Batch的依赖目标下,为了能够统计均值方差,很自然地把同层内所有神经元的响应值作为统计范围,那么我们能否进一步将统计范围缩小?对于CNN明显是可以的,因为同一个卷积层内每个卷积核会产生一个输出通道,而每个输出通道是一个二维平面,也包含多个激活神经元,自然可以进一步把统计范围缩小到单个卷积核对应的输出通道内部。图4展示了CNN中的Instance Normalization,对于图中某个卷积层来说,每个输出通道内的神经元会作为集合S来统计均值方差。对于RNN或者MLP,如果在同一个隐层类似CNN这样缩小范围,那么就只剩下单独一个神经元,输出也是单值而非CNN的二维平面,这意味着没有形成集合S,所以RNN和MLP是无法进行Instance Normalization操作的,这个很好理解。

图4. CNN中的Instance Normalization
我们回想下的CNN中的Batch Normalization,可以设想一下:如果把BN中的Batch Size大小设定为1,此时和Instance Norm的图4比较一下,是否两者是等价的?也就是说,看上去Instance Normalization像是Batch Normalization的一种Batch Size=1的特例情况。但是仔细思考,你会发现两者还是有区别的,至于区别是什么读者可自行思考。
Instance Normalization对于一些图片生成类的任务比如图片风格转换来说效果是明显优于BN的,但在很多其它图像类任务比如分类等场景效果不如BN。
3 Group Normalization
从上面的Layer Normalization和Instance Normalization可以看出,这是两种极端情况,Layer Normalization是将同层所有神经元作为统计范围,而Instance Normalization则是CNN中将同一卷积层中每个卷积核对应的输出通道单独作为自己的统计范围。那么,有没有介于两者之间的统计范围呢?通道分组是CNN常用的模型优化技巧,所以自然而然会想到对CNN中某一层卷积层的输出或者输入通道进行分组,在分组范围内进行统计。这就是Group Normalization的核心思想,是Facebook何凯明研究组2017年提出的改进模型。
图5展示了CNN中的Group Normalization。理论上MLP和RNN也可以引入这种模式,但是还没有看到相关研究,不过从道理上考虑,MLP和RNN这么做的话,分组内包含神经元太少,估计缺乏统计有效性,猜测效果不会太好。
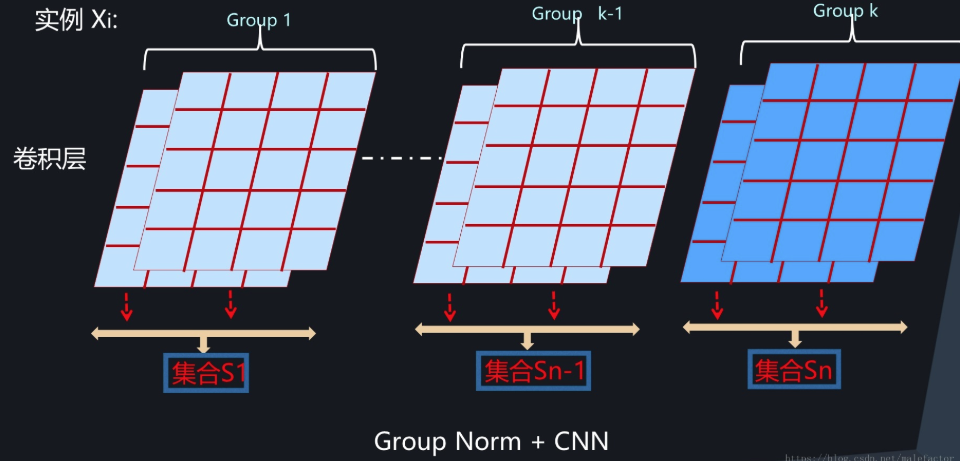
图5. CNN中的Group Normalization
Group Normalization在要求Batch Size比较小的场景下或者物体检测/视频分类等应用场景下效果是优于BN的。

