DFS(深度优先搜索)和BFS(广度优先搜索)
深度优先搜索算法(Depth-First-Search)
深度优先搜索算法(Depth-First-Search),是搜索算法的一种。它沿着树的深度遍历树的节点,尽可能深的搜索树的分支。
当节点v的所有边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。
这一过程一直进行到已发现从源节点可达的所有节点为止。
如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
深度优先搜索是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。
这一过程一直进行到已发现从源节点可达的所有节点为止。
如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
深度优先搜索是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。
DFS属于盲目搜索
深度优先遍历图算法步骤:
- 访问顶点v;
- 依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
- 若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
实例:
DFS 在访问图中某一起始顶点 v 后,由 v 出发,访问它的任一邻接顶点 w1;再从 w1 出发,访问与 w1邻 接但还没有访问过的顶点 w2;然后再从 w2 出发,进行类似的访问,… 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点 u 为止。
接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点。如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止。
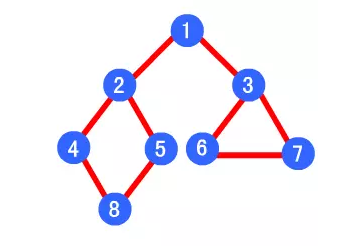
例如下图,其深度优先遍历顺序为 1->2->4->8->5->3->6->7
广度优先搜索算法(Breadth-First-Search)
广度优先搜索算法(Breadth-First-Search),是一种图形搜索算法。
简单的说,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。
如果所有节点均被访问,则算法中止。
BFS同样属于盲目搜索。
一般用队列数据结构来辅助实现BFS算法。
算法步骤:
- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。如果找到目标,则结束搜寻并回传结果。否则将它所有尚未检验过的直接子节点加入队列中。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
- 重复步骤2。
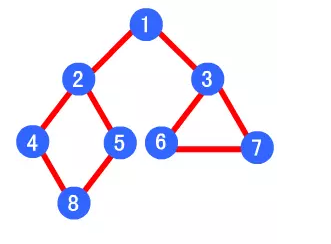
如下图,其广度优先算法的遍历顺序为:1->2->3->4->5->6->7->8
import java.util.ArrayDeque;
public class BinaryTree {
static class TreeNode{
int value;
TreeNode left;
TreeNode right;
public TreeNode(int value){
this.value=value;
}
}
TreeNode root;
public BinaryTree(int[] array){
root=makeBinaryTreeByArray(array,1);
}
/**
* 采用递归的方式创建一颗二叉树
* 传入的是二叉树的数组表示法
* 构造后是二叉树的二叉链表表示法
*/
public static TreeNode makeBinaryTreeByArray(int[] array,int index){
if(index<array.length){
int value=array[index];
if(value!=0){
TreeNode t=new TreeNode(value);
array[index]=0;
t.left=makeBinaryTreeByArray(array,index*2);
t.right=makeBinaryTreeByArray(array,index*2+1);
return t;
}
}
return null;
}
/**
* 深度优先遍历,相当于先根遍历
* 采用非递归实现
* 需要辅助数据结构:栈
*/
public void depthOrderTraversal(){
if(root==null){
System.out.println("empty tree");
return;
}
ArrayDeque<TreeNode> stack=new ArrayDeque<TreeNode>();
stack.push(root);
while(stack.isEmpty()==false){
TreeNode node=stack.pop();
System.out.print(node.value+" ");
if(node.right!=null){
stack.push(node.right);
}
if(node.left!=null){
stack.push(node.left);
}
}
System.out.print("\n");
}
/**
* 广度优先遍历
* 采用非递归实现
* 需要辅助数据结构:队列
*/
public void levelOrderTraversal(){
if(root==null){
System.out.println("empty tree");
return;
}
ArrayDeque<TreeNode> queue=new ArrayDeque<TreeNode>();
queue.add(root);
while(queue.isEmpty()==false){
TreeNode node=queue.remove();
System.out.print(node.value+" ");
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
System.out.print("\n");
}
/**
* 13
* / \
* 65 5
* / \ \
* 97 25 37
* / /\ /
* 22 4 28 32
*/
public static void main(String[] args) {
int[] arr={0,13,65,5,97,25,0,37,22,0,4,28,0,0,32,0};
BinaryTree tree=new BinaryTree(arr);
tree.depthOrderTraversal();
tree.levelOrderTraversal();
}
}

