玻尔兹曼机和受限玻尔兹曼机

玻尔兹曼机

如果发生串扰或陷入局部最优解，Hopfield神经网络就不能正确地辨别模式，如下图。

而玻尔兹曼机（Boltzmann Machine）则可以通过让每个单元按照一定的概率分布发生状态变化，来避免陷入局部最优解。

玻尔兹曼机保持了Hopfield神经网络的假设：

权重对称

自身无连接

二值输出

波尔兹曼机的输出是按照某种概率分布决定的：

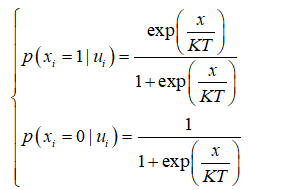
𝑇(>0)表示温度系数，当 𝑇 趋近于无穷时，无论𝑢𝑖取值如何，𝑥𝑖等于 1 或 0 的概率都是  1/2  ，这种状态称为稳定状态。

温度系数越大，跳出局部最优解的概率越高；但是温度系数增大时，获得能量函数极小值的概率就会降低。

反之，温度系数减小时，虽然获得能量函数极小值的概率增加了，但是玻尔兹曼机需要经历较长时间才能达到稳定状态。

 

玻尔兹曼机选择模拟退火算法：

可以先采用较大的温度系数及进行粗调，然后逐渐减小温度系数进行微调。

根据下式求得 𝑇 的极小值：

 

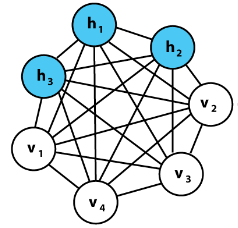
实际应用上，玻尔兹曼机还可以由可见单元和隐藏单元共同构成。

隐藏单元与输入数据没有直接联系，但会影响可见单元的概率。

假设可见单元为可见变量 𝑣 ，隐藏单元为隐藏变量 ℎ 。

玻尔兹曼机含有隐藏变量时，概率分布仍然与前面计算的结果相同。

 

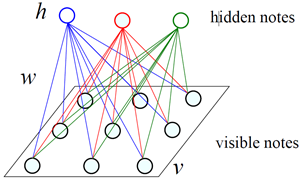
受限玻尔兹曼机

含有隐藏变量的波尔兹曼机训练非常困难，所以辛顿等人提出了受限玻尔兹曼机（Restricted Boltzmann Machine）。

由可见层和隐藏层构成

层内单元之间无连接

信息可双向流动

 

受限波尔兹曼机的能量函数为：

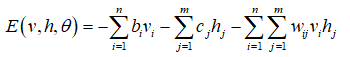
其中，𝑏𝑖是可见变量的偏置， 𝑐𝑗是隐藏变量的偏置，𝑤𝑖𝑗是连接权重，θ是表示所有连接权重和偏置的参数集合。可见变量𝑣_𝑖和隐藏变量ℎ_𝑗的乘积即表示两者之间的相关程度，其与连接权重一致时，能够得到参数的最大似然估计量。

 

改良后的受限玻尔兹曼机会产生庞大的计算量。

要想解决这个问题，可以使用Gibbs采样（Gibbs Sampling）算法进行迭代计算求近似解。但即使这样处理，迭代次数也仍然非常多。于是，人们提出了对比散度算法。

 

(这篇之后继续补充)