BP原理 - 前向计算与反向传播实例
Outline
很多事情不是需要聪明一点,而是需要耐心一点,踏下心来认真看真的很简单的。
假设有这样一个网络层:

第一层是输入层,包含两个神经元i1 i2和截距b1;
第二层是隐含层,包含两个神经元h1 h2和截距b2,
第三层是输出o1,o2,每条线上标的wi是层与层之间连接的权重,激活函数默认为sigmoid函数。
赋初值为:
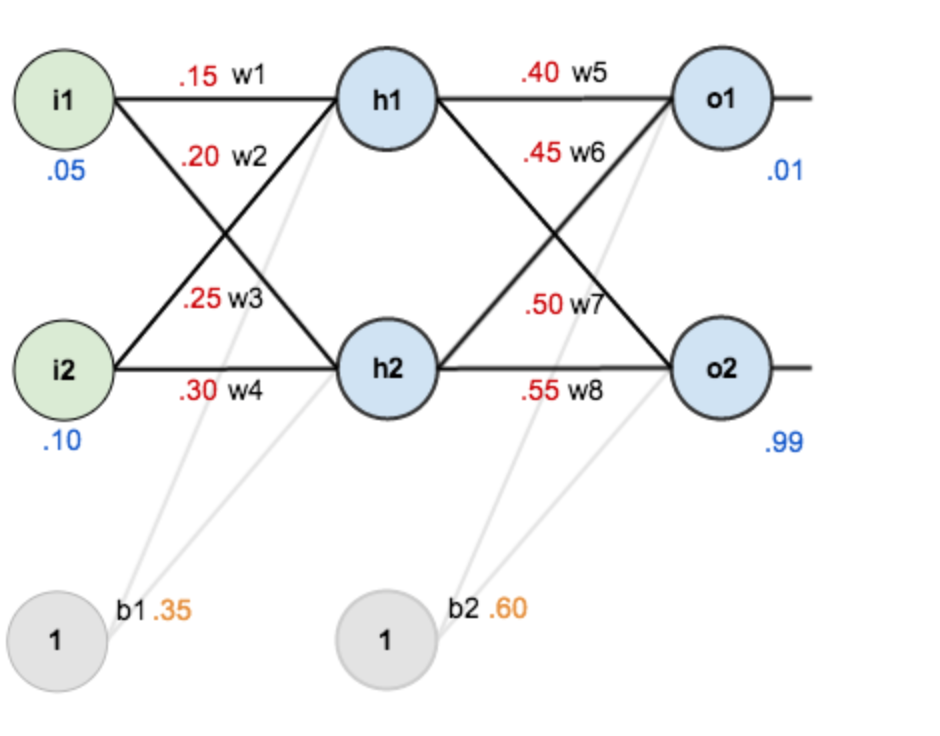
输入数据 i1=0.05,i2=0.10;
输出数据 o1=0.01, o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.55
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
Step 1 前向计算
1. 输入层—>隐含层:
计算神经元h1的输入加权和:

神经元h1的输出o1:(此处用到激活函数为sigmoid函数):

同理,可计算出神经元h2的输出o2:
![]()
2. 隐含层—>输出层:
计算输出层神经元o1的值:

同理,计算o2:
![]()
前向计算过程结束,得到输出值为[0.75136079 , 0.772928465],与实际值[0.01 , 0.99]相差很远,对误差进行反向传播,更新权值,重新计算输出。
Step 2 反向传播
1. 计算总误差
总误差:(square error)
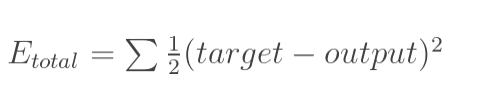
分别计算o1和o2的误差,总误差为两者之和:


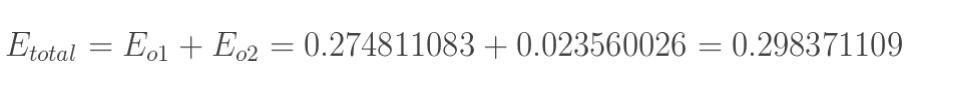
2. 输出层—>隐含层的权值更新
以权重参数w5为例,如果想知道w5对整体误差产生了多少影响,用整体误差对w5求偏导求出:(链式法则)

如图所示:

现在分别计算每个式子的值: loss--Sigmoid--weight
计算![]() :
:

计算下一步之前,先来看一下Sigmoid函数求导:
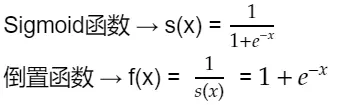
根据倒数法则从f(x)开始推导得出:
![]()
![]()
有以上两个式子可推出:
![]()
计算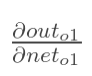 :
:

计算 :
:
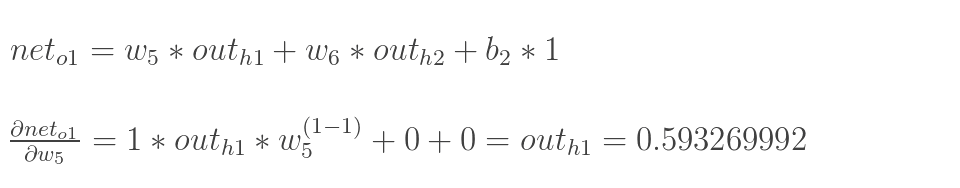
最后三者相乘:

这样我们就计算出整体误差E(total)对w5的偏导值。
综合以上四步计算过程可得:

为了表达方便,用![]() 来表示输出层的误差:
来表示输出层的误差:

因此,整体误差E(total)对w5的偏导公式可以写成:

如果输出层误差计为负的话,也可以写成:

最后,更新w5的值,![]() 是学习速率,这里设为0.5:
是学习速率,这里设为0.5:
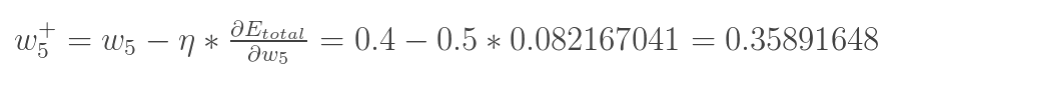
同理,可更新w6,w7,w8:

3. 隐含层—>输入层的权值更新
上一部分传播过程为:out(o1)—>net(o1)—>w5;
此处:out(h1)—>net(h1)—>w1,注意out(h1)会接受E(o1)和E(o2)两个地方传来的误差,两个都要计算。
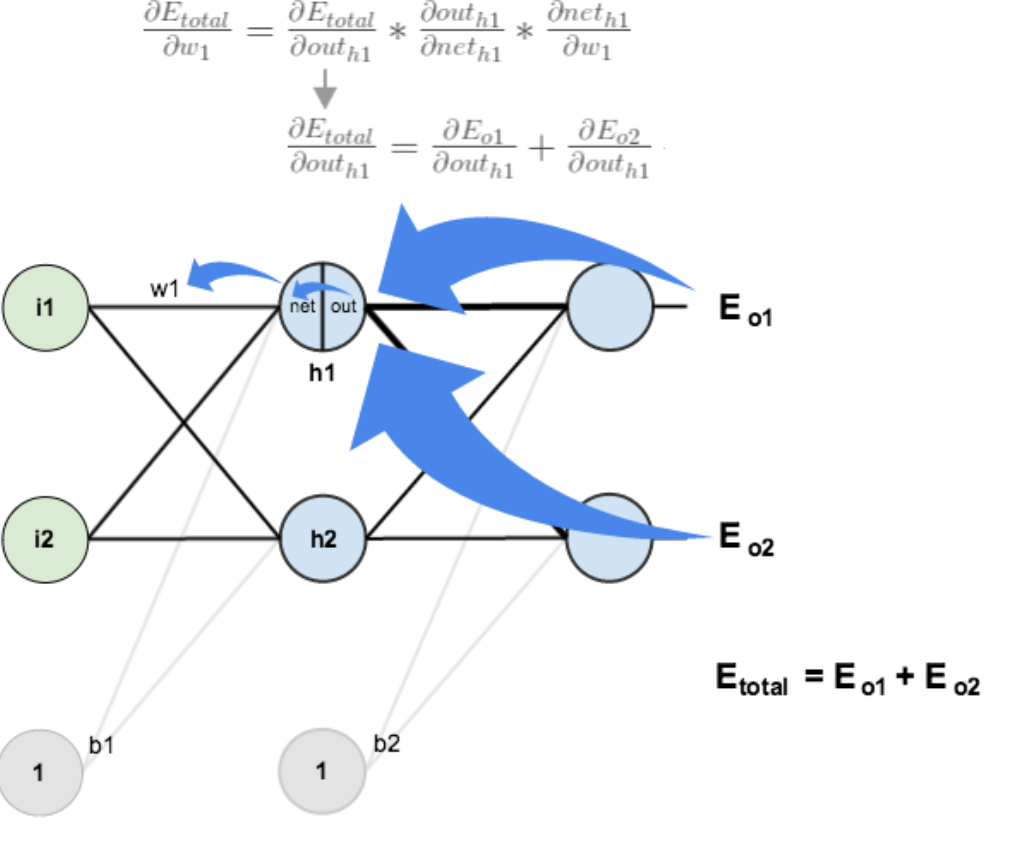
计算![]() :
:

先计算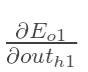 :
:
![]()
![]()
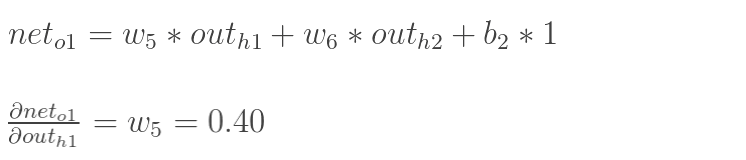
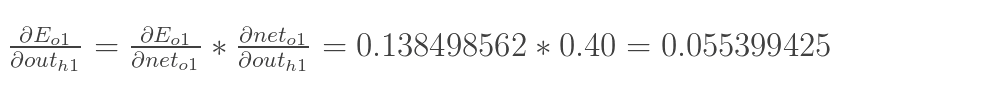
同理,计算出:
![]()
两者相加得到总值:
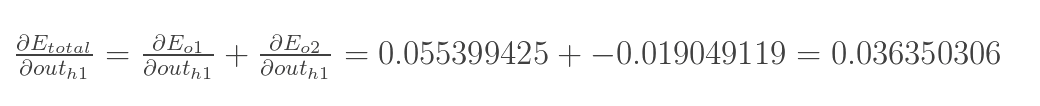
再计算![]() :
:

再计算![]() :
:

最后,三者相乘:

为了简化公式,用sigma(h1)表示隐含层单元h1的误差:

最后,更新w1的权值:
![]()
同理,额可更新w2,w3,w4的权值:

一次误差的反向传播完成,之后再把更新的权值重新计算,得到新的误差,该例中第一次迭代之后,总误差E(total)由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为[0.015912196,0.984065734](原输入为[0.01,0.99])。
