强化学习复习笔记
Outline
Actor-Critic
学习价值函数,也学习策略。
使用Critic减少方差:
蒙特卡洛策略梯度具有高方差。
使用critic来评估动作- 价值函数:
![]()
Actor-critic 算法包含两组参数:
Critic 更新动作 -价值函数参数 w
Actor 更新策略参数 θ, 更新方向由 critic 提供
使用近似策略梯度:
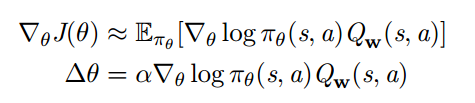
Critic 的作用是: 策略评估
当前参数 θ 下策略 πθ 的表现如何?
例如 蒙特卡洛策略评估 时间差分学习 TD(λ)
也可以使用例如最小二乘策略评估法
基于动作 -价值的 Actor-Critic

使用线性价值函数逼近器Qw(s, a) = ϕ(s, a)Tw , Critic线性TD(0)更新w,Actor策略梯度更新θ
使用逼近的方法计算策略梯度会引入偏差 ,带有偏差的策略梯度不一定能学到正确的解。
如果选择合理的价值函数逼近器,可以有效避免偏差问题,也就是说仍然能沿着正确的策略梯度训练 。
兼容的函数逼近
定理
如果下面两个条件能够满足:
1 价值函数逼近器对策略是兼容的
2 价值函数的参数 w 最小化均方误差
那么基于价值的策略梯度和真实的策略梯度是相同的
证明 :
如果一组参数 w 能够最小化均方误差, 那么 ε 关于 w 的梯度一 定等于零

所以 Qw(s, a) 能够直接代入到策略梯度公式中
![]()
Actor(玩家):为了玩转这个游戏得到尽量高的reward,需要一个策略:输入state,输出action,即上面的第2步。(可以用神经网络来近似这个函数。剩下的任务就是如何训练神经网络,得更高的reward。这个网络就被称为actor)
Critic(评委):因为actor是基于策略policy的所以需要critic来计算出对应actor的value来反馈给actor,告诉他表现得好不好。所以就要使用到之前的Q值。(当然这个Q-function所以也可以用神经网络来近似。这个网络被称为critic。)
Actor 基于概率选行为, Critic 基于 Actor 的行为评判行为的得分, Actor 根据 Critic 的评分修改选行为的概率。
Actor Critic 优点:可以进行单步更新, 相较于传统的PG回合更新要快。
Actor Critic 缺点:Actor的行为取决于 Critic 的Value,但是因为 Critic本身就很难收敛和actor一起更新的话就更难收敛了。
(为了解决收敛问题, Deepmind 提出了 Actor Critic 升级版 Deep Deterministic Policy Gradient,后者融合了 DQN 的优势,解决了收敛难的问题。)
target一个是期望,一个是均方误差。
优势函数
使用基准 (Baseline) 减小方差:
在策略梯度公式中减去一个基准函数 B(s) ,这样可以在不改变期望的前提下有效减小方差。

减去一个基准函数不会对结果训练目标有影响。
一个比较好的基准函数是状态价值函数 B(s) = Vπθ(s) 因此可以使用优势函数Aπθ(s, a) 重新定义策略梯度公式
优势函数就是原来的Q函数减去一个基准函数
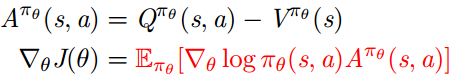
估计优势函数
优势函数可以明显减小策略梯度的方差(中心化)
所以 critic 应该以估计优势函数作为目标
例如同时估计 Vπθ(s) 和 Qπθ(s, a)
使用两个函数逼近器和两组参数向量
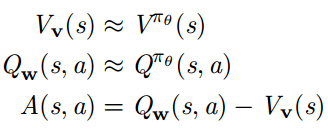
使用例如 TD 学习的方法同时对两个价值函数更新
对于真实的价值函数 Vπθ(s), TD 误差 δπθ
![]()
是关于优势函数的无偏估计
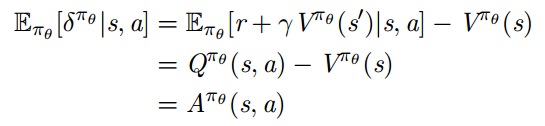
所以我们可以使用 TD 误差来计算策略梯度
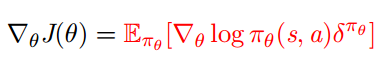
在实际应用中会使用近似的 TD 误差
![]()
这种方法只需要一组 critic 参数 v
不同时间尺度的 Critics
Critic 可以从不同的时间尺度, 以多种目标来估计价值函数Vv(s)
回顾:
对 MC, 目标是回报 vt![]()
对 TD(0), 目标是 TD 目标 r + γVv(s′)![]()
对前向 TD(λ), 目标是 λ-回报 Gλ t![]()
对后向 TD(λ), 使用资格迹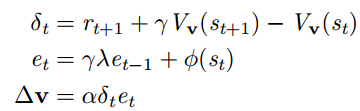
不同时间尺度的 Actors
策略梯度同样可以在不同的时间尺度下进行估计![]()
蒙特卡洛策略梯度法基于完整的回报计算误差![]()
Actor-critic 策略梯度法使用一步 TD 误差
![]()
策略梯度 + 资格迹
和前向 TD(λ) 一样, 策略梯度可以混合使用不同的时间尺度![]()
其中 Gλ t - Vv(st) 是关于优势函数有偏差的估计
同后向 TD(λ) 一样, 可以使用资格迹,使用 ϕ(s) = rθ log πθ(s, a) 替代原始 TD(λ) 算法

这种更新方式可以应用于在线问题, 非完整的序列
其它的策略梯度方差
梯度上升算法可以沿着任意一个上升的方向
一个好的上升方向可以显著加速收敛过程
一个策略可以使用不同的参数表示, 但是动作选择概率可以保持不变
例如在 softmax 策略中对所有的动作都增加它们的得分
基本梯度 (vanilla gradient) 法容易受这类多种参数表示的影响
自然策略梯度

自然策略梯度和参数独立无关
它是对策略做一个微小, 固定的改变后, 寻找与基本梯度最接近的上升方向
![]()
其中 Gθ 是 Fisher 信息矩阵
![]()
自然 Actor-Critic
使用兼容的函数逼近

所以自然策略梯度简化为
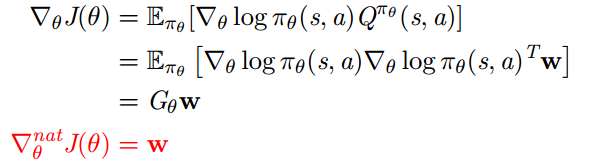
即 actor 参数的更新方向等于 critic 参数
策略梯度算法总结
策略梯度具有多种等价的表示形式

每种都可以对应一个随机梯度上升算法
Critic 使用策略评估 (例如 MC 或 TD 学习法) 来估计Qπ(s, a), Aπ(s, a), Vπ(s)
