特征分解

 

特征分解（eigendecomposition）是使用最广的矩阵分解之一，即我们将矩阵分解成一组特征向量和特征值。

方阵 A 的 特征向量（eigenvector）是指与 A 相乘后相当于对该向量进行缩放的非零向量 v： 

标量 λ 被称为这个特征向量对应的 特征值（eigenvalue）。（类似地，我们也可以 定义 左特征向量（left eigenvector） v^⊤A = λv^⊤，但是通常我们更关注 右特征向量 （right eigenvector））。 

如果 v 是 A 的特征向量，那么任何缩放后的向量 sv (s ∈ R， s ≠ 0) 也是 A 的 特征向量。此外， sv 和 v 有相同的特征值。基于这个原因，通常我们只考虑单位特征向量。

假设矩阵 A 有 n 个线性无关的特征向量 {v⁽¹⁾,...,v⁽ⁿ⁾}，对应着特征值{λ₁, ..., λ_n}。我们将特征向量连接成一个矩阵，使得每一列是一个特征向量： V =  [v⁽¹⁾,...,v⁽ⁿ⁾]. 类似地，我们也可以将特征值连接成一个向量 λ = [λ₁, ..., λ_n]^⊤。 因此 A 的 特征分解（eigendecomposition）可以记作

* diag(λ）向量λ在n*n的方针的对角线上。

正交矩阵的转置和逆矩阵相等

设A是对称矩阵
A^T = A
A^-1 = (A^T)^-1 = (A^-1)^T (即A的逆也是对称矩阵)

 

我们已经看到了构建具有特定特征值和特征向量的矩阵，能够使我们在目标方向上延伸空间。然而，我们也常常希望将矩阵分解（decompose）成特征值和特征向量。这样可以帮助我们分析矩阵的特定性质。不是每一个矩阵都可以分解成特征值和特征向量。在某些情况下，特征分解存在，但是会涉及复数而非实数。在深度学习中，我们通常只需要分解一类有简单分解的矩阵。具体来讲，每个实对称矩阵都可以分解成实特征向量和实特征值：

其中 Q 是 A 的特征向量组成的正交矩阵， Λ 是对角矩阵。特征值 Λ_i,i 对应的特征向量是矩阵 Q 的第 i 列，记作 Q_:,i。因为 Q 是正交矩阵，我们可以将 A 看作沿方 向 v⁽ⁱ⁾ 延展 λ_i 倍的空间。如图 2.3 所示的例子。

 

虽然任意一个实对称矩阵 A 都有特征分解，但是特征分解可能并不唯一。如果两个或多个特征向量拥有相同的特征值，那么在由这些特征向量产生的生成子空间中，任意一组正交向量都是该特征值对应的特征向量。因此，我们可以等价地从这些特征向量中构成 Q 作为替代。按照惯例，我们通常按降序排列 Λ 的元素。在该约定下，特征分解唯一当且仅当所有的特征值都是唯一的。

矩阵的特征分解给了我们很多关于矩阵的有用信息。矩阵是奇异的当且仅当含 有零特征值。实对称矩阵的特征分解也可以用于优化二次方程 f(x) = x⊤Ax，其中 限制 ∥x∥2 = 1。当 x 等于 A 的某个特征向量时， f 将返回对应的特征值。在限制条 件下，函数 f 的最大值是最大特征值，最小值是最小特征值。

所有特征值都是正数的矩阵被称为 正定（positive definite）；所有特征值都是非负数的矩阵被称为 半正定（positive semidefinite）。同样地，所有特征值都是负数的矩阵被称为 负定（negative definite）；所有特征值都是非正数的矩阵被称为 半负定 （negative semidefinite）。 半正定矩阵受到关注是因为它们保证 x^⊤Ax ≥ 0。此外， 正定矩阵还保证 x^⊤Ax = 0 → x = 0。

 

正交矩阵

正交化

如果是实对称矩阵，那么它的不同特征值的特征向量必然正交。

 

 

 

求解特征值和特征向量

一、特征值和特征向量的概念和计算

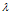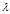    明确定义：设A是n阶方阵，如果存在常数及非零n向量x，使得，则称是矩阵A的特征值，x是A属于特征值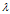的特征向量。给定n阶矩阵A，行列式

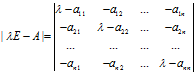
的结果是关于的一个多项式，成为矩阵A的特征多项式，该特征多项式构成的方程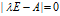称为矩阵A的特征方程。

 

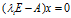　　定理：n阶矩阵A的n个特征值就是其特征方程的n个跟；而A的属于特征值的特征向量就是齐次线性方程的非零解。

齐次线性方程：

　　例：求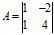的特征值和特征向量

　　解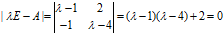：，解一元二次方程可得，；

　　　　对应的特征向量为x满足，求得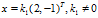

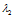　　　　对应的特征向量为x满足，求得

二、特征值和特征向量的几何意义

1、矩阵、向量、向量的矩阵变换

　　在进行特征和特征向量的几何意义解释之前，我们先回顾一下向量、矩阵、向量矩阵变换的等相关知识。

　　向量有行向量和列向量，向量在几何上被解释成一系列与轴平行的位移，一般说来，任意向量v都能写成"扩展"形式：

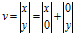
　　以3维向量为例，定义p、q、r为指向+x，+y和+z方向的单位向量，则有v=xp+yq+zr。现在向量v就被表示成p、q、r的线性变换了。这里的基向量是笛卡尔积坐标轴，但事实上这个一个坐标系可以由任意的3个基向量定义，只要这3个基向量线性无关就行（不在同一平面上）。因此，用一个矩阵乘以向量，如Ax，表述如下：

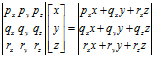
　　如果把矩阵的行解释为坐标系的基向量，矩阵与向量相乘（或向量与矩阵相乘）相当于执行一次坐标转换，Ax=y可表述为x经矩阵A变换后变为y。因此，追溯矩阵的由来，与向量的关系，我们会觉得矩阵并不神秘，它只是用一种紧凑的方式来表达坐标转换所需的数学运算。

2、矩阵的特征值和特征向量

　　矩阵A的特征值和特征向量分别为和x，记为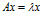，该式子可理解为向量x在几何空间中经过矩阵A的变换后得到向量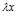。由此可知，向量x经过矩阵A变换后，方向并无改变（反方向不算方向改变），只是伸缩了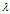倍。

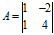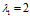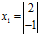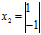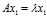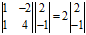　　以矩阵为例，其特征向值分别为，，对应的特征向量为，，那么（）表示向量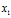经过矩阵A变换后，得到，向量变换变为改变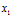方向，知识将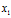在原方向上扩充了2倍。特征值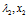也是同样道理，经过矩阵A变换后特征向量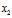在原方向上扩充了3倍。

　　因此，将特征向量看成基向量，矩阵就是这些基向量向对应的特征值伸展所需的数学运算。给定一个矩阵，就可以找出对应的基（特征向量），及透过向量变换（矩阵），这些基的伸展（特征值）。

三、特征值和特征向量的应用实例

1、主成分分析（Principle Component Analysis, PCA）

（1）方差、协方差、相关系数、协方差矩阵

    方差：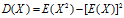

    协方差： , ,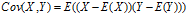 

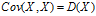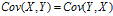
    **方差是衡量单变量的离散程度，协方差是衡量两个变量的相关程度（亲疏），协方差越大表明两个变量越相似（亲密），协方差越小表明两个变量之间相互独立的程度越大。

    相关系数：，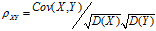

    **协方差和相关系数都可以衡量两个表明的相关程度，协方差未消除量纲，不同变量之间的协方差大小不能直接比较，而相关系数消除了量纲，可以比较不同变量之间的相关程度。

    协方差矩阵：如果有两个变量X，Y，那么协方差矩阵为，协方差阵说明了样本中变量间的亲疏关系。

（2）主成分分析的思想和算法

　　主成分分析是利用降维的思想，将多个变量转化为少数几个综合变量（即主成分），其中每个主成分都是原始变量的线性组合，各主成分之间互不相关，从而这些主成分能够反映始变量的绝大部分信息，且所含的信息互不重叠。它是一个线性变换，这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。主成分分析经常用减少数据集的维数，同时保持数据集的对方差贡献最大的特征。

　　假设用p个变量来描述研究对象，分别用X₁，X₂…X_p来表示，这p个变量构成的p维随机向量为X=(X₁，X₂…X_p)，n个样本构成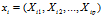组成了n行p列的矩阵A。主成分求解过程如下：

　　第一步，求解得到矩阵A的协方差阵B；

　　第二步，求解协方差阵B，得到按大小顺序排列的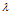特征值向量，为特征值向量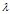中每个特征值组成的对角矩阵，U为所有特征值对应的特征向量构成的矩阵U，因此有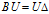。重点来了，U是有特征向量构成的正定阵，向量的每一行可以视为一个的基向量，这些基向量经过矩阵B转换后，得到了在各个基向量上的伸缩，伸缩的大小即为特征向量。

第三步，主成分个数选择，根据特征值的大小，将特征值较大的作为主成分，其对应的特征向量就为基向量，特征值的筛选根据实际情况而定，一般大于1即可考虑作为主成分。

（3）实例分析——机器学习中的分类问题

　　机器学习中的分类问题，给出178个葡萄酒样本，每个样本含有13个参数，比如酒精度、酸度、镁含量等，这些样本属于3个不同种类的葡萄酒。任务是提取3种葡萄酒的特征，以便下一次给出一个新的葡萄酒样本的时候，能根据已有数据判断出新样本是哪一种葡萄酒。

问题详细描述：http://archive.ics.uci.edu/ml/datasets/Wine
训练样本数据：http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data

把数据集赋给一个178行13列的矩阵R，它的协方差矩阵C是13行13列的矩阵，对C进行特征分解，对角化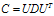，其中U是特征向量组成的矩阵，D是特征之组成的对角矩阵，并按由大到小排列。然后，令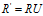，就实现了数据集在特征向量这组正交基上的投影。嗯，重点来了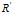，中的数据列是按照对应特征值的大小排列的，后面的列对应小特征值，去掉以后对整个数据集的影响比较小。比如，现在我们直接去掉后面的7列，只保留前6列，就完成了降维。

　　下面我们看一下降维前和降维后的使用svm分类结果，本部分采用实现SVM的R语言包e1071，代码如下表所示。分类结果显示，使用主成分分析后的样本和未进行主成分分析样本的分类结果一样。因此，主成分分析提取的6个主成分能较好的表达原样本的13个变量。

library("e1071")
#读取数据
wineData=read.table("E:\\blog\\特征值和特征向量\\data.csv",header=T,sep=",");

#计算协方差阵
covariance = cov(wineData[2:14])

#计算特征值和特征向量
eigenResult=eigen(covariance)

#选取6个主成分,并计算这6个主成分解释的方差总和
PC_NUM = 6
varSum=sum(eigenResult$values[1:PC_NUM])/sum(eigenResult$values)

#降维后的样本
ruduceData= data.matrix(wineData[2:14])%*%eigenResult$vectors[,1:PC_NUM]

#加入分类标签
#finalData=cbind(wineData$class,ruduceData)

#给finalData添加列名
#colnames(finalDat) =c("calss","pc1","pc2","pc3","pc4","pc5","pc6")

#训练样本--主成分分析后的样本作为训练样本
y=wineData$class;
x1=ruduceData;
model1 <- svm(x1, y,cross=10)
pred1 <- predict(model1, x1)
#pred1 <- fitted(model1)
table(pred1, y) #使用table来查看预测结果

#训练样本--原数据作为训练样本
x2=wineData[2:14]
model2 <- svm(x2, y,cross=10)
#pred2 <- predict(model2, x2)
pred2 <- fitted(model2)
table(pred2, y) #使用table来查看预测结果