数据结构 —— 哈希函数，散列表

名词解释

 

1.关键字 Key

一个序列，用{} 表示。例如，{10，2，23}

 

2.散列函数 / 哈希表

某种映射方式，例如， H(Key) = Key%10

注意，这里的 MOD 后面这个数字 10，实际含义是，留出 10 个 Slot。

 

3.放在外存/主存 中的数组，其位置编号由 散列函数 决定。

11%10 = 1 

21%10 = 1

这种现象，称为“冲突”；

11 和 21 这个元素，称为  “同义词” 。

 

用链表连接的，叫做 【拉链法】，或者【链接法】，或者【链地址法】。

 

4.平均成功查找长度 

ASL_successful = （1+2+3+4+1+2+1+2+1+1+2+1）/12

其中，12 是元素个数。举个例子，如果搜“27”，要经历 3 次搜到 “27”。

 

平均失败查找长度 

ASL_fail = （0+4+0+2+0+0+2+1+0+0+2+1+0）/13 

注意，这种算法不是所有场景都合适。为什么呢？

 

5.举个例子

 

先看答案吧！

 

 

 

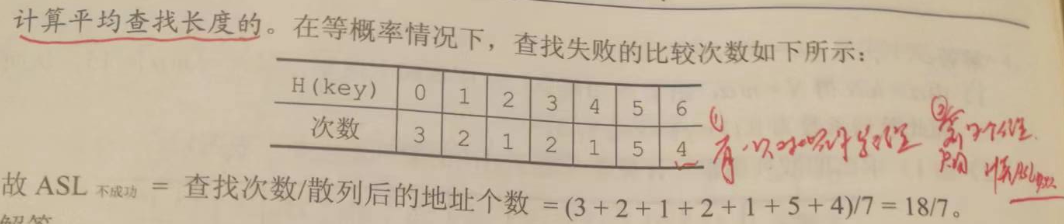
首先来解释一下，这道题目的平均成功查找长度，和平均失败查找长度。

平均成功查找长度，由物理存储区域计算得到。

因此，发现 【14】多比较了一次，因为编号0，放在 1号位置。

【18】和【9】，分别各自多比较了  两次。

因此，7个元素，按照道理，对比7次；因为冲突，多比较了 5 次（1+2+2），故成功找到存放位置的对比次数为 12次。

平均成功查找长度 = 12 / 7

7 是元素个数。

 

然后，关于平均失败查找长度。和王道课上讲得有些不一样。

1）这道题，有位置限制。注意到，H(key) = key % 7

注意到，7 是散列函数的钥匙，即留给这个 集合/数组 的位置。因此，如果出现冲突，即便元素的位置编号超出了，也只能算到 0 - 6号。

2）因此，某个位置，有多少个元素来 “报道”（对比）过。另外注意，元素存入，和对比分开算。例如，7存在0号，14（本该存在0号的）存在1号。这样的话，7元素对比、存入，命中2次；14元素对比，命中1次；0号位置共对比3次。

14元素存在1号，对比、存入，命中2次，1号未知对比2次。依次类推。

注意到 6 号位置，因为 9元素对比一次之后，另一次对比在 7号位置发生，所以，对比次数比 5号位置少 1 次。

 

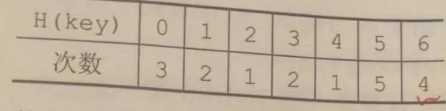
因此，平均失败查找长度 = （3+2+1+2+1+5+4） / 7 = 18/7

 

 

5. 如果位置充分的时候怎么办？ 

所谓位置充分，也就是散列函数的确定问题。例如，H(key) = key % 15

这个时候，你有10个元素，显然不会冲突。

 

看一道王道视频课的例题。

 

这种方式，ShoelessCai 自己命名为 By Layer

And, By Slots is like ....

 

 

注意：

1.成功查找率，无需考虑冲突。但是 平均失败查找长度，要考虑冲突的次数

2.装填因子 = 关键字个数 / 表长  —— 影响查找效率

 

参考：

https://www.cnblogs.com/ygsworld/p/10238729.html

https://blog.csdn.net/weixin_43305485/article/details/120680371

https://www.cnblogs.com/qixinbo/p/7782314.html 

 

 

 

如何处理冲突？

 

 

 

 

 

ShoelessCai.com 值得您的关注！