计算机组成原理 | 王道 -数据的表示和运算 真题
这个也是实时更新的，更新完结之后，我会在帖子开启的部分说明
2023年12月3日
今天中午吃完午饭，放松了一个小时，由于这几年没有收入，我非常有罪恶感。然后前段时间发现也有一个木有收入的媒体人，转发一下吧。
南开 + 腾讯 + 背包客 + 自媒体 + 网络红人 —— 暂时厘定这些标签
参考
https://www.bilibili.com/video/BV1PP4y1G7t9/?spm_id_from=333.999.0.0
开始复习了！
【2009】冯诺依曼计算机中，指令和数据均以二进制形式存放在存储器中，CPU区分它们的依据是（）
A 指令操作吗的译码结果
B 指令和数据的寻址方式
C 指令周期的不同阶段
D 指令和数据所在的存储单元
答案：C
解析：
计算机有专门的取指令的时间间隔，识别出该时间间隔，可知道是 A 还是 D
【2016】将高级语言源程序转换为机器级目标代码文件的程序是（）
A 汇编程序
B 链接程序
C 编译程序
D 解释程序
答案：C
背出来吧！！
【2015】冯诺依曼结构计算中，数据采用二进制编码表示，其主要原因是（）
I 二进制的运算规则简单
II 制造两个稳态的物理器件较容易
III 便于用逻辑门电路实现算术运算
A 仅 I、II
B 仅 I、III
C 仅 II、III
D I、II 和 III
【2010】下列选项中，能缩短程序执行时间的措施是（）
I 提高 CPU 时钟频率
II 优化数据通路结构
III 对程序进行编译优化
A 仅 I 和 II
B 仅 I 和 III
C 仅 II 和 III
D I、II 和 III
答案：D
背出来吧！！
【2011】下列选项中，描述浮点数操作速度指标的是（）
A MIPS
B CPI
C IPC
D MFLOPS
答案：D
解析：
每百万浮点数操作
【2013】某计算机主频为 1.2GHz ，其指令分为 4 类，它们在基准程序中所占比例及 CPI 如下表所示：
该机器的 MIPS 是（）
A 100
B 200
C 400
D 600
答案：C
加权平均的 MIPS
【2012】假定基准程序 A 在某计算机上的运行时间为 100s，其中，90s 为 CPU 时间，其余为 I/O 时间。若 CPU 速度提高 50%，I/O 速度不变，则运行基准程序 A 所耗费的时间是 （）。
A 55s B 60s C 65s D 70s
答案：D
解析：
1. 时间结构 90 + 10 秒
2. 前半段 CPU 速度提高 50%，即 1.5v，工作总量不变，速度 1.5 倍，时间为 1/1.5；
3. 90 / 1.5 + 10 = 70 秒
【2014】程序 P在机器 M上的执行时间是 20s，编译优化后，P执行的指令数减少到原来的 70%，而 CPI增加到原来的 1.2倍，则P在M上的执行时间是 （）。
A 8.4s B 11.7s C 14s D 16.8s
答案：D
解析：
1.假设原来 CPI = x, 现在 1.2 x
2.主频 f ，程序所需的 clock = 20秒 * f ，于是 #instrct = 20 f / x
3.调整后， 0.7 #instruct = time * f /(1.2x)
4.解上述方程组 time = 16.8
* 注意：其他变量可不解出
【2017】假定计算机 M1 和 M2 具有相同的指令集体系结构（ISA），主频分别为 1.5GHz 和 1.2GHz 。在 M1 和 M2 上运行某基准程序 P 平均 CPI 分为 2 和 1，则程序 P 在 M1 和 M2 上运行时间的比值是（）
A 0.4 B 0.625 C 1.6 D 2.5
答案：C
解析：
1.#instruct 一致。依据 “具有相同的指令集体系结构”
2.#instruct * CPI / f 就是时间指标
3.2/1.5 ： 1/1.2 = 1.6
【2013】用海明码对长度为 8 位的数据进行检错、纠错时，其海明码为（）。
A 2 B 3 C 4 D 5
答案：C
解析：
1.数据位 D = 8
2.海明不等式 2^r - r >= 8 + 1 , r=4。因此需要 4 位校验位。
【2009】一个 C 语言程序在一台 32 位机器上运行，程序中定义了三个变量 x、y、z，其中 x 和 z 为 int 型，y 为 short 型。当 x = 127、y = -9 时，执行赋值语句 z=x+y 后，x、y、z 的值分别是（）。
A x=0000007FH，y=FFF9H，z=00000076H
B x=0000007FH，y=FFF9H，z=FFFF0076H
C x=0000007FH，Y=FFF7H，z=FFFF0076H
D x=0000007FH，y= FFF7H，z=00000076H
答案：D
解析：
1.x = 7FH 左端 0 补齐
2.y = F7H 左端 1 补齐
3.z= x+y = 118 未溢出。
z = 76H
【2010】 假定有 4个整数用8位补码分别表示 r1=FEH、r2=F2H、r3 = 90H、r4 = F8H，若将运算结果存放在一个8位寄存器中，则下列运算会发生溢出的是 ( )。
A r1*r2
B r2*r3
C r1*r4
D r2*r4
答案：B
解析：
1.用十进制计算，查看是否超出 - 128 - 127
2.r1=- 2 r2=-14 r3=-112 r4=-8
3.最大两个数字相乘： r2*r3 = 1568 超过 8 位存储
【2012】某计算机存储器按字节编址，采用小端方式存放数据。假定编译器规定 int 和 short 型长度分别为 32 位和 16 位，并且数据按边界对齐存储，某 C 语言程序如下：
struct {
int a;
char b;
short c;
} record;
record.a = 273;
若 record 变量的首地址为 0xC008，则都照顾 0xC008 中的内容及 record.c 的地址分别为（）。
A 0x00, 0xC00D
B 0x00, 0xC00E
C 0x11, 0xC00D
D 0x11, 0xC00E
答案：D
解析：
1.首先要知道 abc 三个变量在 机器中存放的样子
a = 256 + 16 + 1
存放形态 0000 0000 0000 0000 0000 0001 0001 0001
机器数 00000111
2.小端存放，交叉放置
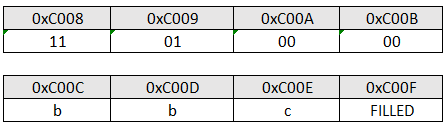
3.注意：小端一定是交叉的，字节填充，这两个考点！
【2012】假定编译器规定 int 和 short 类型长度分别为 32 和 16 位，执行下列 C 语言语句：
unsigned short x=65530;
unsigned int y=x;
得到 y 的机器数为i（）
A 0000 7FFAH
B 0000 FFFAH
C FFFF 7FFAH
D FFFF FFFAH
答案：B
解析：
1.unsigned short = 1111 1111 1111 1010
无符号数是这样的，如果全 1 表示 2^(16) - 1 = 65535
2.unsigned int = 0000 0000 0000 0000 1111 1111 1111 1010
机器数 0 0 0 0 F F F A H
【2016】有如下 C 语言程序段：
short si = -32767
unsigned short usi = si;
执行上述条件之后， usi 值为（）
A -32767
B 32767
C 32768
D 32769
答案：D
解析：
1.short 形式 1111 1111 1111 1111 = -32768
存放形式，1000 0000 0000 0001
unsigned short，没有负数，为 2^(15)+1 = 32769 。
【2013】某字长为 8 位的计算机中，已知整型变量 x、y 的机器数分别为 [X]补 = 1 111 0100 ，[Y]补 = 1 011 0000。若整型变量 z = 2x + y/2 ，则 z 的机器数为（）。
A 1 100 0000
B 0 010 0100
C 1 010 1010
D 溢出
答案：A
解析：
1.补码移位的时候，符号位 不动；
2.负数补码，左移 + 0 ，右移 + 1
2.2x = 1 110 1000 y/2 = 1 101 1000
上述两个数字相加，得到 1100 0000 。
【2014】若 x=103，y=-25，则下列表达式采用 8 位定点补码运算实现时，会发生溢出的是（）。
A x+y B -x+y C x-y D -x-y
答案：C
解析：
1.这道题挺有意思的，因为定点补码范围 -128 - 127。因此 ，等价命题就是，结果是否在范围里面。
2.x-y=128 超出范围的； y-x = -128 在范围内。因此 选择 C
【2015】由 3 个 “1” 和 5 个 “0” 组成的 8 位二进制补码，能表示的最小整数是 ( )。
A .-126 B -125 C -32 D -3
答案：B
解析：
1.第一个位是1，0尽量放在右边
2.1000 0011 表示 - 125
选择B
【2016】某计算机字长为 32 位，按字节编址，采用小端方式存放数据。假定有一个 double 型变量，其机器数表示为 1122 3344 5566 7788H，存放在 0000 8040H 开始的连续存储单元中，则存储单元 0000 8046H 中存放的是（）。
A 22H B 33H C 77H D 66H
答案：A
解析：
1.小端存取，一定交叉。
2.存放位置如下。
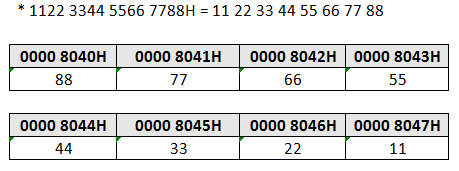
3.注意到，这个数据，一定是尾端放在靠前的地址。总结为，小端存取，一定交叉。
【2018】假定有符号整数采用补码表示，若 int 型变量 x 和 y 机器数分别是 FFFF FFDFH 和 0000 0041H ，则 x, y 的值及 x - y 的机器数分别是（）。
A x=-65， y=41， x - y 的机器数溢出
B x=-33。 y=65，x - y 机器数 FFFF FF9DH
C x=-33， y=65，x - y 机器数 FFFF FF9EH
D x=-65， y=-41，x - y 机器数 FFFF FF96H
答案：C
解析：
转换成 二进制 即可
【2018】某32位计算机按字节编址，采用小端方式。若语句“int i = 0;” 对应指令的机器代码为 “C7 45 FC 00 00 00 00”，则语句“int i=-64;” 对应指令的机器代码是 ( )。
A C7 45 FC C0 FF FF FF
B C7 45 FC 0C FF FF FF
C C7 45 F0 FF FF FF C0
D C7 45 FC FF FF FF 0C
答案：A
解析：
1.因为 int 是 32 位，因此只有地位的 32 位是数据位，前面的部分，认为是操作码。
2.小端存储，一定交叉。
3.int i=-64
1111 1111 1111 1111 1111 1111 1100 0000
FFFF FFC0
4.存放形式 C0 FF FF FF
【2018】整数 x 机器数 1101 1000，分别对 x 进行逻辑右移 1 位和算术右移 1 位操作，得到的机器数各是（）
A 1110 1100， 1110 1100
B 0110 1100， 1110 1100
C 1110 1100， 0110 1100
D 0110 1100， 0110 1100
答案：B
解析：
1.打算盘有正负，因此算术右移，符号位不动。
2.逻辑右移 0110 1100
算术右移，负数补码，添加 1 。1110 1100
3.因此 选择 B
【2011】假定一个 8 位字长的 C程序中，运行如下 C 程序段：
unsigned int x=134;
unsigned int y=246;
int m=x;
int n=y;
unsigned int z1-x-y;
unsigned int z2=x+y;
int k1=m-n;
int k2=m+n;
若编译器编译 时将 8 个 8 位寄存器 R1 - R8 分别分配给变量 x,y,m,n,z1,z2,k1,k2。请回答下列问题（有符号整数用补码表示）。
（1）执行上述程序段之后，寄存器 R1 ，R5 和 R6 内容分别是什么（用十六进制表示）？
（2）执行上述程序段之后，变量 m 和 k1 的值分别是多少（用十进制表示）？
（3）上述程序段涉及有符号整数加减、无符号整数加减运算，这四则运算能否用同一个加法器辅助电路实现？简述理由。
（4）计算机内部如何判断有符号整数加减运算的结果是否发生溢出？上述程序段中，哪些有符号整数运算语句的执行结果会发生溢出。
答案：R1=86H， R5=90H， R6=7CH
（1）
对于十进制而言，R1=x, R5=z1, R6=z2。
x -- 0000 0000 0000 0000 0000 0000 1000 0110
x-y = - 112
x+y = 380
R1 = 86H
R5 = 1001 0000 H= 90H
R6 = 7CH
关于 R6，答案是直接二进制加法，x = 1000 0110 , y = 1111 0110 全部正数
R6 = x+y = 0111 1100 = 7CH
这里的关键点在于，最高位 1 舍去，不显示。至少在计算机中是这样的，因此用十进制加减，可能会出错！
（2）m = 1 111 1010B = -122
k1 = 1 001 0000B = - 112
int m = 1000 0110 = - 111 1010 = -122
int n = 1111 0110 = - 000 1010 = - 10
int k1 = m-n = -122 - (-10) = -112 = 1 001 0000
（3）能用同一套加法器电路。
n 位无符号整数加减，可以在 n 位加法器中实现；
n 位有符号整数加减，可以在 n 位加法器中实现。
（4）第一种，就是查看结果符号，单独查看。第二种，用两位符号位，如果两位符号位不一致，溢出。
最后一条语句执行时候，溢出。
int k2 = -122 + (-10) = -132
这里很有意思，虽然 int 是 32 位的，但是题目明确说了，是 8 个 8 位寄存器，因此 k2 只有 8 个比特。
此时 int 范围 -128-127，因此 k2 溢出。
Needless to say 记住 C语言中的变量类型强制转换顺序：
最后运算结果：double
4种数据类型转换： char - int - long - double
【2009】浮点数加减运算过程一般包含对阶、尾数运算、规格化、舍入和溢出判断等步骤。设浮点数的阶码和尾数均用补码表示，且位数分别为 5 和 7（均含两位符号位）。若有两个数 X = 2^7 * 29 / 32 和 Y = 2^5 * 5 / 8，则用浮点加法计算 X + Y 的最终结果 （）
A 00111 1100010
B 00111 0100010
C 01000 0010001
D 发生溢出
答案：D
解析：
1.浮点数运算步骤，按照题目意思，如下：
X：阶码 00111； 001 1101.00001
Y：阶码 00101；000 0101.00100
2.注意到，位数只有 7 个 DIGITS
X省掉部分精度，变成： 00111 + 5[10] ； 111 0100
Y尾数需要移动小数点：00101 + 3[10] ； 101 0010
3.算到第二步就发现溢出了。为什么？因为中间 【阶码】 位数不够！
4.留个思考题，这个思路对吗？
完成这道题目的复习的时候，还有一些不会，翻阅2019年王道考研视频课。
首先，二进制小数点移动的时候，尾数部分缩小，阶数部分放大。如果尾数左移一个 DIGIT，那么阶码（指数）则+1。
考察视频课中的，变量 b 。
【2010】假定变量 i, f, d 数据类型分别为 int, float, double （int 用补码表示， float, double 分别用 IEEE 754 单精度和双精度浮点数格式表示），已知 i=785, f=1.5678E3, d=1.5E100，若在32位机器中执行下列关系表达式，则结果为 “真“ 的是（）
(1) i=(int)(float)i
(2) f=(float)(int)f
(3) f=(float)(double)f
(4) (d+f)-d=f
A 仅 1 和 2
B 仅 1 和 3
C 仅 2 和 3
D 仅 3 和 4
答案：B
解析：
1.这个是 C 语言语法，满足就近原则
2. 强制类型转换，先定义的变量，先分配物理空间。因此，(float)(double) i
3.上述定义语句，先定义为 double，再转换成 float 。结果为 TRUE。
如果说，(float)(int)i 这类语句，结果 FALSE，因为转换成 float 会空间不够而改变其真值。
【2011】float 型数据通常用 IEEE754 单精度浮点格式表示。若编译器将 float 型变量 x 分配在一个 32 位浮点寄存器 FR1 中，且 x = -8.25 ，则 FR1 的内容是 （）
A C104 0000H
B C242 0000H
C C184 0000H
D C1C2 0000H
答案：A
解析：
1.IEEE754 浮点格式 1-8-23
2.依据 x 的十进制
x= - 1000.01 = - 1.00001 * 2^(3) -- STEP1 易错
阶码 E = 3 + 127 = 130 -- STEP2
尾数 M = 0.00001 -- STEP2
x = 1, 100 0001 0, 000 0100 0000 0000 0000 0000 -- STEP3
3.4个 DIGITS 一组
C104 0000H -- STEP4
4.自己第三遍解答的时候做错。错在哪呢？不能直接转换为阶码，一定要按步骤！
【2012】float 类型 （即 IEEE754 单精度浮点数格式）能表示的最大正整数（）
A 2^126 - 2^103
B 2^127 - 2^104
C 2^127 - 2^103
D 2^128 - 2^104
答案：D
解析：
1.阶码最多 254 位，即阶码部分 1DIGIT【0】 + 7DIGITS【1】， E -127 = 127 幂指数的值。
2.位数，最大正数，尾数 23DIGITS【1】， x + 2^(-23) = 2^(0) + 1 推导出 x = 2 - 2^(-23)
浮点数大小 2^127(2-2^(-23)) = 2^(128) - 2^(104) 最大正数。
总结：
1.这类题要注意，DIGITS 变化。
2.IEEE754 中间的阶码是没有符号位的，范围是 1-254 （0-255 往中间收缩一个 DIGIT），可以表示的幂指数 -126 - 127。
3.进一步地，IEEE754 FLOAT 形式，最小数值 1.0*2^(-126) 。
【2013】某数采用 IEEE754 单精度浮点数格式表示为 C640 0000H，则该数值是 （）
A -1.5 * 2^(13)
B -1.5 * 2^(12)
C -0.5 * 2^(13)
D -0.5 * 2^(12)
答案：A
解析：
1.首先，展开成二进制
1, 100 0110 0, 100 0000 0000 0000 0000 0000
符号：负数
阶码
128 + 8 + 4 = 140
140 - 127 = 13
尾数 1 + 1*2^(-1) = 1.5
2.最终数值
- 1.5 * 2^(13)
【2014】float 型数据常用 IEEE754 单精度浮点格式表示。假设两个 float 变量 x 和 y 分别存放在 32 位寄存器 f1 和 f2 中，若 (f1) = CC90 0000H，(f2) = B0C0 0000H ，则 x 和 y 之间的关系 （）
A x < y 且符号相同
B x < y 且符号不同
C x > y 且符号相同
D x > y 且符号不同
答案：A
解析：
1.先变成二进制
f1 = 1, 100 1100 1, 001 0000 0000 0000 0000 0000
f2 = 1, 011 0000 1, 100 0000 0000 0000 0000 0000
2.显然符号相同
f1 阶码
128 + 16 + 8 + 1 = 153
E = 153 - 127 = 26
M = 1 + 1/8 = 1.125
综上，f1 = - 1.125 * 2^(26)
f2 阶码
64 + 32 + 1 = 97
E = 97 - 127 = -30
M = 1 + 1/2 = 1.5
综上， f2 = - 1.5 * 2^(-30)
3.比较大小
符号一致 x < y ，注意，x 和 y 当中的值分别为 f1 和 f2。
几个结论记一记：
1. 舍入不一定产生误差；
2. 浮点数注意补码存储。其中，包括算术右移时候，关注符号，补码负数右移，添加“1”。
3. 浮点数加减法。对阶 - 尾数相加 - 尾数左右移动及调整阶码（例如，右移阶码+1）
例题
【2015】下列有关浮点数加减运算的叙述中，正确的是i（）
（I）对阶操作不会引起阶码上溢或下溢
（II）右规和尾数舍入都可能引起阶码上溢
（III）左规时可能引起阶码下溢
（IV）尾数溢出时结果不一定溢出
A 仅 II，III
B 仅 I，II，IV
C 仅 I，III，IV
D I，II，III，IV
答案：D
解析：
1. 对阶是小的向大的看齐，显然不会溢出；
2. 尾数舍入，阶码是可能上溢的；
3. 左规，尾数左移，阶码 -1
右规，尾数右移，阶码 + 1
因此，左规会引起阶码下溢。
4.尾数溢出，去掉精度即可，不引起浮点数（结果）溢出。
【2018】IEEE 754 单精度浮点数格式表示的数中，最小的规格化正数是（）
A 1.0 * 2^(-126)
B 1.0 * 2^(-127)
C 1.0 * 2^(-128)
D 1.0 * 2^(-149)
答案：A
解析：
1.阶码
E 范围1 - 254，幂指数范围 -126 - 127
2.尾数部分全0 ，隐藏 1
综上，IEEE 754 最小正数 = 1.0 * 2^(-126)
这个知识点很重要，请记住！
【2017】已知
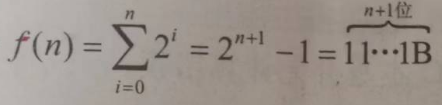
计算 f(n) 的C语言函数 f1 如下：
int f1(unsigned n) {
int sum=1, power=1;
for (unsigned i=0; i<n-1; i++) {
power *= 2;
sum += power;
}
return sum;
}
将 f1 中的 int 都改为 float，可得到计算 f(n) 的另一个函数 f2 。假设 unsigned 和 int 型数据都占 32 位， float 采用 IEEE 754 单精度标准，请回答下列问题：
（1）当 n=0 时，f1 会出现死循环，为什么？若将 f1 中的变量 i 和 n 都定义为 int 型，则 f1 是否还会出现死循环？为什么？
（2）f1(23) 和 f2(23) 返回的值是否相等？机器数各是什么？用十六进制表示。
（3）f1(24) 和 f2(24) 返回值分别为 33 554 和 33 554 432.0 ，为什么不想等？
（4）f1(31) = 2^(32) - 1，而 f1(31) 返回值却为 -1 为什么？若使 f1(n) 返回值 f(n) 相等，则最大的 n 是多少？
（5）f2(127) 机器数为 7F80 0000H，对应的值是什么？若使 f2(n) 结果不溢出，则最大的 n 是多少？ 若使 f2(n) 结果精确（无舍入），则最大的 n 是多少？
答案：
（1）unsigned 和 int 都占据 32 bit，其中，int 是有符号的，而 unsigned 是无符号的。
如果 n=0, n-1 = 1111 1111[2]
当 i 自增到 i = 1111 1111[2]
i++
i = 0000 0000[2]f2(
又开始一次循环！
如果 n 和 i 都变成 int 型，可以避免这个问题。
因为有符号位，这样 n - 1 = -1 可以正确表示并且比较大小，第一轮比较时候，直接跳出循环。
（2）首先。
明确 f2 函数，即函数体中 sum power 均为 float 数据类型。
因此，f1(23)，f2(23) 返回的值相等。
其次。
f1(23) = 2^(23 + 1) - 1 = 2^(24) - 1 （第一个 power 值为 1）
存储形式，24 个 1，而 int 形式 32 bit ，并没有溢出。
再者。
浮点数 float，符号 1位，阶码 8 位，尾数 23 位。足够用于表示 2^(24) - 1
即乘以阶码的 2^(254 - 127 )
最后，写出机器数。
f1(23) = 0000 0000 1111 1111 1111 1111 1111 1111 = 00FF FFFFH
f2(23) = 0, 100 1011 0, 111 1111 1111 1111 1111 1111 = 4B7F FFFFH
符号 0
阶码 E = 23 + 127 = 150
150 = 128 + 16 + 4 + 2
尾数 M = 全1 = 2 - 2^(-23) 具体求法，待定系数法。
（3）f1(24） = f2(24) - 1
主要因为 float 只有 23 个有效位表示精度， n = 24 的时候，需要舍入，舍入使得结果 + 1。
（4）因为对于 int 来说， n=31 时候，需要 32 个bit表示1，机器认为为 -1 。
由此推断，针对 f1() 来说，n 最大为i30。
BTW，这句话的含义是，f1() 和 原本想表达的含义相同。
（5）f2(127) = 7F80 0000H = 0, 111 1111 1, 000 0000 0000 0000 0000 0000B
IEEE 754 规定，阶码全 1，尾数全 0， 表示 inf
其次，IEEE 754 表示，f2 不溢出的最大正整数为 126
第二小题。
使得 f2(n) 获得精确结果， n 最大取 23。
与第一题差异？
理论上， n 可以取到 -126， 大家不会这么干 —— 因为会损失精度。
第二章结束语：至此计算机组成原理i，第二章圆满完成！
ShoelessCai.com 值得您的关注。
