Splay算法基础与习题
前言
Spaly是基于二叉查找树实现的,
什么是二叉查找树呢?就是一棵树呗:joy: ,但是这棵树满足性质—一个节点的左孩子一定比它小,右孩子一定比它大
比如说
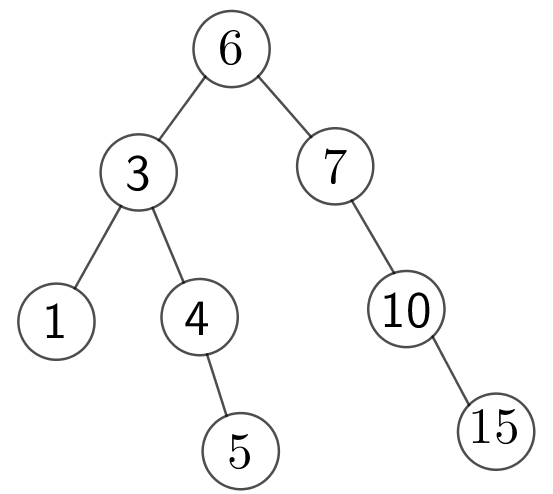
这就是一棵最基本二叉查找树
对于每次插入,它的期望复杂度大约是logn级别的,但是存在极端情况,比如9999999 9999998 9999997.....1这种数据,会直接被卡成n2
在这种情况下,平衡树出现了!
Splay基本操作
rotate
首先考虑一下,我们要把一个点挪到根,那我们首先要知道怎么让一个点挪到它的父节点
情况1
当X是Y的左孩子
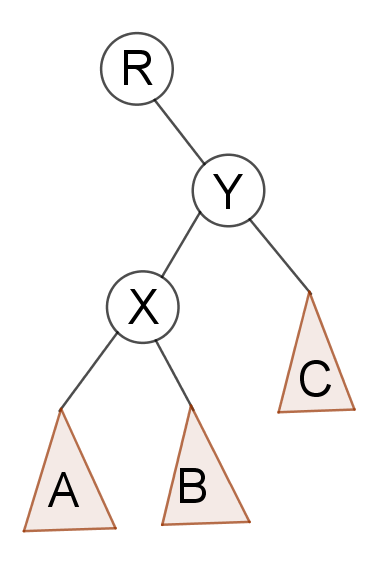
这时候如果我们让X成为Y的父亲,只会影响到3个点的关系
B与X,X与Y,X与R
根据二叉排序树的性质
B会成为Y的左儿子
Y会成为X的右儿子
X会成为R的儿子,具体是什么儿子,这个要看Y是R的啥儿子
经过变换之后,大概是这样
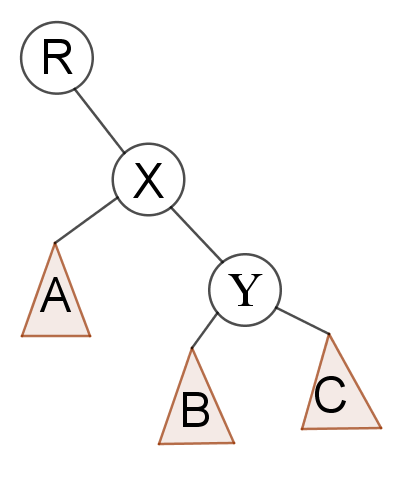
情况2
当X是Y的右孩子
本质上和上面是一样的,
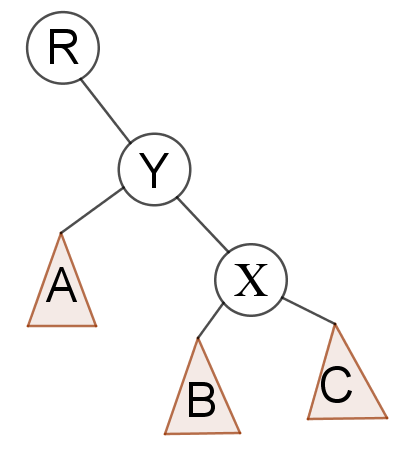
变换后为
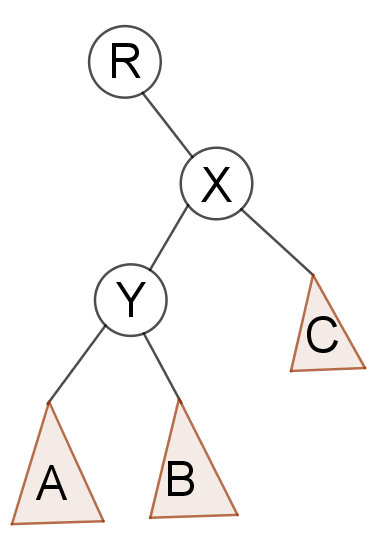
这两种代码单独实现都比较简单,我就不写了(实际上是我懒)
但是这两种旋转情况很类似,第二种情况实际就是把第一种情况的X,Y换了换位置
我们考虑一下能不能将这两种情况合并起来实现呢?
答案是肯定的
首先我们要获取到每一个节点它是它爸爸的哪个孩子,可以这么写
bool ident(int x) { return tree[tree[x].fa].ch[0] == x ? 0 : 1; }
如果是左孩子的话会返回0,右孩子会返回1
那么我们不难得到R,Y,X这三个节点的信息
int Y = tree[x].fa; int R = tree[Y].fa; int Yson = ident(x); //x是y的哪个孩子 int Rson = ident(Y);
B的情况我们可以根据X的情况推算出来,根据^运算的性质,0^1=1,1^1=0,2^1=3,3^1=2,而且B相对于X的位置一定是与X相对于Y的位置是相反的
(否则在旋转的过程中不会对B产生影响)
int B = tree[x].ch[Yson ^ 1];
然后我们考虑连接的过程
根据上面的图,不难得到
B成为Y的哪个儿子与X是Y的哪个儿子是一样的
Y成为X的哪个儿子与X是Y的哪个儿子相反
X成为R的哪个儿子与Y是R的哪个儿子相同
connect(B, Y, Yson); connect(Y, x, Yson ^ 1); connect(x, R, Rson);
connect函数这么写,挺显然的
void connect(int x, int fa, int how) { //x节点将成为fa节点的how孩子 tree[x].fa = fa; tree[fa].ch[how] = x; }
单旋函数就是这样了,利用这个函数就可以实现把一个节点搬到它的爸爸那儿了
splay
splay(x,to)是实现把x节点搬到to节点
最简单的办法,对于x这个节点,每次上旋直到to
但是!
如果你真的这么写,可能会T成SB
下面我们介绍一下双旋的splay
这里的情况有很多,但是总的来说就三种情况
1.to是x的爸爸
if (tree[tree[x].fa].fa == to) rotate(x);
2.x和他爸爸和他爸爸的爸爸在一条线上
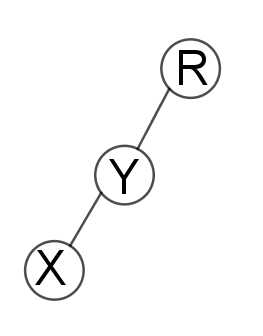
这时候先把Y旋转上去,再把X旋转上去就好
else if (ident(x) == ident(tree[x].fa)) rotate(tree[x].fa), rotate(x);
3.x和他爸爸和他爸爸的爸爸不在一条线上
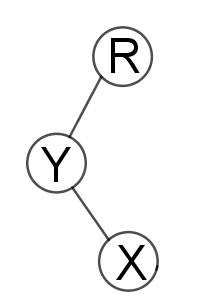
这时候把X旋转两次就好
总的代码:
void splay(int x, int to) { to = tree[to].fa; while (tree[x].fa != to) { if (tree[tree[x].fa].fa == to) rotate(x); else if (ident(x) == ident(tree[x].fa)) rotate(tree[x].fa), rotate(x); else rotate(x), rotate(x); } }
Splay的实现
结构体与变量定义
struct node { int v;//权值 int fa;//父亲节点 int ch[2];//0代表左儿子,1代表右儿子 int rec;//这个权值的节点出现的次数 int sum;//子节点的数量 }; int tot;//tot表示不算重复的有多少节点
rotate
void rotate(int x) { int Y=fa(x),R=fa(Y); int Yson=ident(x),Rson=ident(Y); connect(T[x].ch[Yson^1],Y,Yson); connect(Y,x,Yson^1); connect(x,R,Rson); update(Y);update(x); }
splay
void splay(int x,int to) { to=fa(to); while(fa(x)!=to) { int y=fa(x); if(T[y].fa==to) rotate(x); else if(ident(x)==ident(y)) rotate(y),rotate(x); else rotate(x),rotate(x); } }
插入
int newnode(int v,int f) { T[++tot].fa=f; T[tot].rec=T[tot].sum=1; T[tot].val=v; return tot; } void insert(int x) { int now=root; if(root==0) {newnode(x,0);root=tot;}// else { while(1) { T[now].sum++; if(T[now].val==x) {T[now].rec++;splay(now,root);return ;} int nxt=x<T[now].val?0:1; if(!T[now].ch[nxt]) { int p=newnode(x,now); T[now].ch[nxt]=p; splay(p,root);return ; } now=T[now].ch[nxt]; } } }
删除
int find(int x) { int now=root; while(1) { if(!now) return 0; if(T[now].val==x) {splay(now,root);return now;} int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; } } void delet(int x) { int pos=find(x); if(!pos) return ; if(T[pos].rec>1) {T[pos].rec--,T[pos].sum--;return ;} else { if(!T[pos].ch[0]&&!T[pos].ch[1]) {root=0;return ;} else if(!T[pos].ch[0]) {root=T[pos].ch[1];T[root].fa=0;return ;} else { int left=T[pos].ch[0]; while(T[left].ch[1]) left=T[left].ch[1]; splay(left,T[pos].ch[0]); connect(T[pos].ch[1],left,1); connect(left,0,1);// update(left); } } }
查询x数的排名
int rak(int x) { int now=root,ans=0; while(1) { if(T[now].val==x) return ans+T[T[now].ch[0]].sum+1; int nxt=x<T[now].val?0:1; if(nxt==1) ans=ans+T[T[now].ch[0]].sum+T[now].rec; now=T[now].ch[nxt]; } }
查询排名为x的数
int kth(int x)//排名为x的数 { int now=root; while(1) { int used=T[now].sum-T[T[now].ch[1]].sum; if(T[T[now].ch[0]].sum<x&&x<=used) {splay(now,root);return T[now].val;} if(x<used) now=T[now].ch[0]; else now=T[now].ch[1],x-=used; } }
求x的前驱
int lower(int x) { int now=root,ans=-INF; while(now) { if(T[now].val<x) ans=max(ans,T[now].val); int nxt=x<=T[now].val?0:1;//这里需要特别注意 now=T[now].ch[nxt]; } return ans; }
求x的后继
int upper(int x) { int now=root,ans=INF; while(now) { if(T[now].val>x) ans=min(ans,T[now].val); int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; } return ans; }
完整模板
#include<bits/stdc++.h> #define ls(x) T[x].ch[0] #define rs(x) T[x].ch[1] #define fa(x) T[x].fa #define root T[0].ch[1] using namespace std; const int MAXN=1e5+10,mod=10007,INF=1e9+10; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin)),p1==p2?EOF:*p1++; } struct node { int fa,ch[2],val,rec,sum; }T[MAXN]; int tot=0,pointnum=0; void update(int x){T[x].sum=T[ls(x)].sum+T[rs(x)].sum+T[x].rec;} int ident(int x){return T[fa(x)].ch[0]==x?0:1;} void connect(int x,int fa,int how){T[fa].ch[how]=x;T[x].fa=fa;} void rotate(int x) { int Y=fa(x),R=fa(Y); int Yson=ident(x),Rson=ident(Y); connect(T[x].ch[Yson^1],Y,Yson); connect(Y,x,Yson^1); connect(x,R,Rson); update(Y);update(x); } void splay(int x,int to) { to=fa(to); while(fa(x)!=to) { int y=fa(x); if(T[y].fa==to) rotate(x); else if(ident(x)==ident(y)) rotate(y),rotate(x); else rotate(x),rotate(x); } } int newnode(int v,int f) { T[++tot].fa=f; T[tot].rec=T[tot].sum=1; T[tot].val=v; return tot; } void insert(int x) { int now=root; if(root==0) {newnode(x,0);root=tot;}// else { while(1) { T[now].sum++; if(T[now].val==x) {T[now].rec++;splay(now,root);return ;} int nxt=x<T[now].val?0:1; if(!T[now].ch[nxt]) { int p=newnode(x,now); T[now].ch[nxt]=p; splay(p,root);return ; } now=T[now].ch[nxt]; } } } int find(int x) { int now=root; while(1) { if(!now) return 0; if(T[now].val==x) {splay(now,root);return now;} int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; } } void delet(int x) { int pos=find(x); if(!pos) return ; if(T[pos].rec>1) {T[pos].rec--,T[pos].sum--;return ;} else { if(!T[pos].ch[0]&&!T[pos].ch[1]) {root=0;return ;} else if(!T[pos].ch[0]) {root=T[pos].ch[1];T[root].fa=0;return ;} else { int left=T[pos].ch[0]; while(T[left].ch[1]) left=T[left].ch[1]; splay(left,T[pos].ch[0]); connect(T[pos].ch[1],left,1); connect(left,0,1);// update(left); } } } int rak(int x) { int now=root,ans=0; while(1) { if(T[now].val==x) return ans+T[T[now].ch[0]].sum+1; int nxt=x<T[now].val?0:1; if(nxt==1) ans=ans+T[T[now].ch[0]].sum+T[now].rec; now=T[now].ch[nxt]; } } int kth(int x)//排名为x的数 { int now=root; while(1) { int used=T[now].sum-T[T[now].ch[1]].sum; if(T[T[now].ch[0]].sum<x&&x<=used) {splay(now,root);return T[now].val;} if(x<used) now=T[now].ch[0]; else now=T[now].ch[1],x-=used; } } int lower(int x) { int now=root,ans=-INF; while(now) { if(T[now].val<x) ans=max(ans,T[now].val); int nxt=x<=T[now].val?0:1;//这里需要特别注意 now=T[now].ch[nxt]; } return ans; } int upper(int x) { int now=root,ans=INF; while(now) { if(T[now].val>x) ans=min(ans,T[now].val); int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; } return ans; } int main() { int t; cin>>t; while(t--) { int opt,x; cin>>opt>>x; if(opt==1) insert(x); else if(opt==2) delet(x); else if(opt==3) printf("%d\n",rak(x)); else if(opt==4) printf("%d\n",kth(x)); else if(opt==5) printf("%d\n",lower(x)); else if(opt==6) printf("%d\n",upper(x)); } return 0; }
Splay区间问题
splay搞区间问题非常简单,比如我们要在区间l,r上搞事情,那么我们首先把l的前驱旋转到根节点
再把r的后继旋转到根节点的右儿子
那么此时根节点的右儿子的左儿子所代表的就是区间l,r
这个应该比较好理解
然后就可以像线段树的lazy标记一样,给区间l,r打上标记,延迟更新,比如区间反转的时候更新的时候直接交换左右儿子
这里有一个技巧:如果一个区间被打了两次,那么就相当于不打
所以我们用一个bool变量来储存该节点是否需要被旋转
下传函数可以这么写
inline void pushdown(int x) { if(tree[x].rev) { swap(tree[x].ch[0],tree[x].ch[1]); tree[tree[x].ch[0]].rev^=1; tree[tree[x].ch[1]].rev^=1; tree[x].rev=0; } }
模板例题
讲解链接:https://www.cnblogs.com/shmilky/p/14099376.html


