【POJ3171】Cleaning Shifts
线型dp+线段树优化
我们定义f[i]表示覆盖[L,i]的最小代价,我们将牛按照r递增排列,假设当前牛为[ai,bi],代价为vali
那么存在
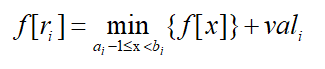
我们在状态转移时,每次需要查询区间内的最值,同时f数组发生更新,因此我们可以用线段树的查询、修改在较快时间内维护f数组。
同时我们注意一下边界的处理即可。

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 typedef long long ll; 7 struct node { 8 int l,r; 9 ll val; 10 }a[86500<<2]; 11 int n,s,t; 12 struct cow { 13 int l,r; 14 ll val; 15 bool operator <(const cow &x) const { 16 return r<x.r; 17 } 18 }c[10010]; 19 void build(int now,int l,int r) { 20 a[now].l=l; 21 a[now].r=r; 22 a[now].val=99999999999; 23 if(l==r) return ; 24 int mid=l+r>>1; 25 build(now<<1,l,mid); 26 build(now<<1|1,mid+1,r); 27 } 28 ll dp[100010]; 29 ll query(int now,int x,int y) { 30 if(x<=a[now].l&&a[now].r<=y) return a[now].val; 31 ll ret=99999999999; 32 int mid=a[now].l+a[now].r>>1; 33 if(x<=mid) ret=min(ret,query(now<<1,x,y)); 34 if(y>mid) ret=min(ret,query(now<<1|1,x,y)); 35 return ret; 36 } 37 void updata(int now,int x,ll val) { 38 if(a[now].l==a[now].r) { 39 a[now].val=val; 40 return ; 41 } 42 int mid=a[now].l+a[now].r>>1; 43 if(x<=mid) updata(now<<1,x,val); 44 else updata(now<<1|1,x,val); 45 a[now].val=min(a[now<<1].val,a[now<<1|1].val); 46 } 47 int main() { 48 scanf("%d%d%d",&n,&s,&t); 49 for(int i=1;i<=n;i++) { 50 scanf("%d%d%lld",&c[i].l,&c[i].r,&c[i].val); 51 } 52 sort(c+1,c+n+1); 53 build(1,1,t+1); 54 memset(dp,0x7f,sizeof(dp)); 55 for(int i=1;i<=n;i++) { 56 if(c[i].r<s) continue ; 57 if(c[i].l<=s) dp[c[i].r]=min(dp[c[i].r],c[i].val); 58 else dp[c[i].r]=min(dp[c[i].r],query(1,c[i].l,c[i].r)+c[i].val); 59 updata(1,c[i].r+1,dp[c[i].r]); 60 } 61 ll ans=99999999999; 62 for(int i=t;i<=c[n].r;i++) { 63 ans=min(ans,dp[i]); 64 } 65 if(ans>=99999999999) puts("-1"); 66 else printf("%lld\n",ans); 67 return 0; 68 }



