阅读翻译Mathematics for Machine Learning之2.7 Linear Mappings

阅读翻译Mathematics for Machine Learning之2.7 Linear Mappings

关于：

• 首次发表日期：2024-07-23
• Mathematics for Machine Learning官方链接： https://mml-book.com
• ChatGPT和KIMI机翻，人工润色
• 非数学专业，如有错误，请不吝指出

2.7 线性映射

在接下来的内容中，我们将研究保持向量空间结构的映射，这将使我们能够定义坐标的概念。在本章的开头，我们提到向量是可以相加和乘以标量的对象，且结果仍然是向量。当应用映射时，我们希望保持这一性质：考虑两个实向量空间 $V,W$。如果映射 $\mathrm{\Phi }:V\to W$ 满足以下条件，则它保持向量空间的结构：

$$\begin{array}{}\text{(2.85)}& \mathrm{\Phi }(\mathit{x}+\mathit{y})& =\mathrm{\Phi }(\mathit{x})+\mathrm{\Phi }(\mathit{y})\text{(2.86)}& \mathrm{\Phi }(\lambda \mathit{x})& =\lambda \mathrm{\Phi }(\mathit{x})\end{array}$$

对于所有 $\mathit{x},\mathit{y}\in V$ 和 $\lambda \in \mathbb{R}$ 成立。我们可以用以下定义来总结这一点：

定义 2.15（线性映射）。对于向量空间 $V,W$，一个映射 $\mathrm{\Phi }:V\to W$ 被称为线性映射（或向量空间同态/线性变换），如果

$$\begin{array}{}\text{(2.87)}& \mathrm{\forall }\mathit{x},\mathit{y}\in V\mathrm{\forall }\lambda ,\psi \in \mathbb{R}:\mathrm{\Phi }(\lambda \mathit{x}+\psi \mathit{y})=\lambda \mathrm{\Phi }(\mathit{x})+\psi \mathrm{\Phi }(\mathit{y})\end{array}$$

结果表明，我们可以将线性映射表示为矩阵（见第 2.7.1 节）。回想一下，我们也可以将一组向量作为矩阵的列。在使用矩阵时，我们必须记住矩阵代表的是什么：是线性映射还是向量的集合。我们将在第 4 章中详细讨论线性映射。在继续之前，我们将简要介绍一些特殊的映射。

定义 2.16（单射、满射、双射）。考虑一个映射 $\mathrm{\Phi }$ : $\mathcal{V}\to \mathcal{W}$，其中 $\mathcal{V}$ 和 $\mathcal{W}$ 可以是任意集合。那么 $\mathrm{\Phi }$ 被称为：

• 单射（Injective），如果 $\mathrm{\forall }\mathit{x},\mathit{y}\in \mathcal{V}$，有 $\mathrm{\Phi }(\mathit{x})=\mathrm{\Phi }(\mathit{y})⟹\mathit{x}=\mathit{y}$。
• 满射（Surjective），如果 $\mathrm{\Phi }(\mathcal{V})=\mathcal{W}$。
• 双射（Bijective），如果它既是单射又是满射。

如果 $\mathrm{\Phi }$ 是满射，那么 $\mathcal{W}$ 中的每个元素都可以通过 $\mathrm{\Phi }$ 从 $\mathcal{V}$ 中“到达”。双射 $\mathrm{\Phi }$ 可以“被逆”，即存在一个映射 $\mathrm{\Psi }$ : $\mathcal{W}\to \mathcal{V}$ 使得 $\mathrm{\Psi }\circ \mathrm{\Phi }(\mathit{x})=\mathit{x}$。这个映射 $\mathrm{\Psi }$ 被称为 $\mathrm{\Phi }$ 的逆映射，通常记作 ${\mathrm{\Phi }}^{-1}$。

有了这些定义，我们介绍以下向量空间 $V$ 和 $W$ 之间的线性映射的特例：

• 同构（Isomorphism）：$\mathrm{\Phi }:V\to W$ 线性且双射
• 自同态（Endomorphism）：$\mathrm{\Phi }:V\to V$ 线性
• 自同构（Automorphism）：$\mathrm{\Phi }:V\to V$ 线性且双射
• 我们定义 ${\mathrm{id}}_V:V\to V,\mathit{x}\mapsto \mathit{x}$ 为 $V$ 中的恒等映射或恒等自同构。

---

**例 2.19（同态（Homomorphism））**

映射 $\mathrm{\Phi }:{\mathbb{R}}^2\to \mathbb{C},\mathrm{\Phi }(\mathit{x})=x_1+i{x}_2$ 是一个同态：

$$\begin{array}{}\text{(2.88)}& \begin{array}{rl}\mathrm{\Phi }(\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{l}{y}_1\\ y_2\end{array}\right])& =(x_1+y_1)+i(x_2+y_2)=x_1+i{x}_2+y_1+i{y}_2\\ & =\mathrm{\Phi }\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)+\mathrm{\Phi }\left(\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]\right)\\ \mathrm{\Phi }\left(\lambda \left[\begin{array}{l}{x}_1\\ x_2\end{array}\right]\right)& =\lambda x_1+\lambda i{x}_2=\lambda (x_1+i{x}_2)=\lambda \mathrm{\Phi }\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right).\end{array}\end{array}$$

这也说明了为什么复数可以表示为 ${\mathbb{R}}^2$ 中的元组：存在一个双射线性映射，可以将 ${\mathbb{R}}^2$ 中元组的逐元素加法转换为对应加法的复数集合。请注意，我们这里只展示了线性性，而不是双射性。

---

定理 2.17（Axler (2015) 的定理 3.59）。有限维向量空间 $V$ 和 $W$ 是同构的，当且仅当 $\dim (V)=\dim (W)$。

定理 2.17 表明，存在一个线性、双射的映射在两个相同维度的向量空间之间。直观上，这意味着相同维度的向量空间在某种程度上是相同的，因为它们可以互相转换而不会遭受任何损失。

定理 2.17 还为我们提供了将 ${\mathbb{R}}^{m\times n}$（$m\times n$ 矩阵的向量空间）和 ${\mathbb{R}}^{mn}$（长度为 $mn$ 的向量的向量空间）视为相同的理由，因为它们的维度都是 $mn$，并且存在一个线性、双射的映射将一个转换为另一个。

备注。考虑向量空间 $V,W,X$。那么：

• 对于线性映射 $\mathrm{\Phi }:V\to W$ 和 $\mathrm{\Psi }:W\to X$，映射 $\mathrm{\Psi }\circ \mathrm{\Phi }:V\to X$ 也是线性的。
• 如果 $\mathrm{\Phi }:V\to W$ 是同构（isomorphism），那么 ${\mathrm{\Phi }}^{-1}:W\to V$ 也是同构。
• 如果 $\mathrm{\Phi }:V\to W,\mathrm{\Psi }:V\to W$ 是线性的，那么 $\mathrm{\Phi }+\mathrm{\Psi }$ 和 $\lambda \mathrm{\Phi },\lambda \in \mathbb{R}$，也是线性的。

2.7.1 线性映射的矩阵表示

任何 $n$ 维向量空间都与 ${\mathbb{R}}^n$ 同构（定理 2.17）。我们考虑一个 $n$ 维向量空间 $V$ 的基 $\{{\mathit{b}}_1,\dots ,{\mathit{b}}_n\}$。在接下来的内容中，基向量的顺序很重要。因此，我们写作

$$\begin{array}{}\text{(2.89)}& B=({\mathit{b}}_1,\dots ,{\mathit{b}}_n)\end{array}$$

并称这个 $n$ 元组为 $V$ 的有序基。

备注（符号）。我们现在使用的符号有点复杂，因此我们在这里总结一些部分。$B=({\mathit{b}}_1,\dots ,{\mathit{b}}_n)$ 是一个有序基，$\mathcal{B}=\{{\mathit{b}}_1,\dots ,{\mathit{b}}_n\}$ 是一个（无序）基，$\mathit{B}=[{\mathit{b}}_1,\dots ,{\mathit{b}}_n]$ 是一个矩阵，其列是向量 ${\mathit{b}}_1,\dots ,{\mathit{b}}_n$。

定义 2.18（坐标）。考虑一个向量空间 $V$ 和其有序基 $B=({\mathit{b}}_1,\dots ,{\mathit{b}}_n)$。对于任何 $\mathit{x}\in V$，我们可以得到一个唯一的表示（线性组合）

$$\mathit{x}={\alpha }_1{\mathit{b}}_1+\dots +{\alpha }_n{\mathit{b}}_n$$

其中 ${\alpha }_1,\dots ,{\alpha }_n$ 是 $\mathit{x}$ 相对于 $B$ 的坐标，并且向量

$$\mathit{\alpha }=\left[\begin{array}{c}{\alpha }_1\\ ⋮\\ {\alpha }_n\end{array}\right]\in {\mathbb{R}}^n$$

是 $\mathit{x}$ 相对于有序基 $B$ 的坐标向量/坐标表示。

一个基实际上定义了一个坐标系。我们熟悉的二维笛卡尔坐标系是由标准基向量 ${\mathit{e}}_1,{\mathit{e}}_2$ 张成的。在这个坐标系中，向量 $\mathit{x}\in {\mathbb{R}}^2$ 有一个表示，它告诉我们如何线性组合 ${\mathit{e}}_1$ 和 ${\mathit{e}}_2$ 来得到 $\mathit{x}$。然而，${\mathbb{R}}^2$ 的任何基都定义了一个有效的坐标系，并且相同的向量 $\mathit{x}$ 在基 $({\mathit{b}}_1,{\mathit{b}}_2)$ 中可能有不同的坐标表示。在图 2.8 中，向量 $\mathit{x}$ 相对于标准基 $({\mathit{e}}_1,{\mathit{e}}_2)$ 的坐标是 $[2,2{]}^{\mathrm{\top }}$。然而，相对于基 $({\mathit{b}}_1,{\mathit{b}}_2)$，相同的向量 $\mathit{x}$ 表示为 $[1.09,0.72{]}^{\mathrm{\top }}$，即 $\mathit{x}=1.09{\mathit{b}}_1+0.72{\mathit{b}}_2$。在接下来的部分中，我们将探讨如何获得这种表示。

---

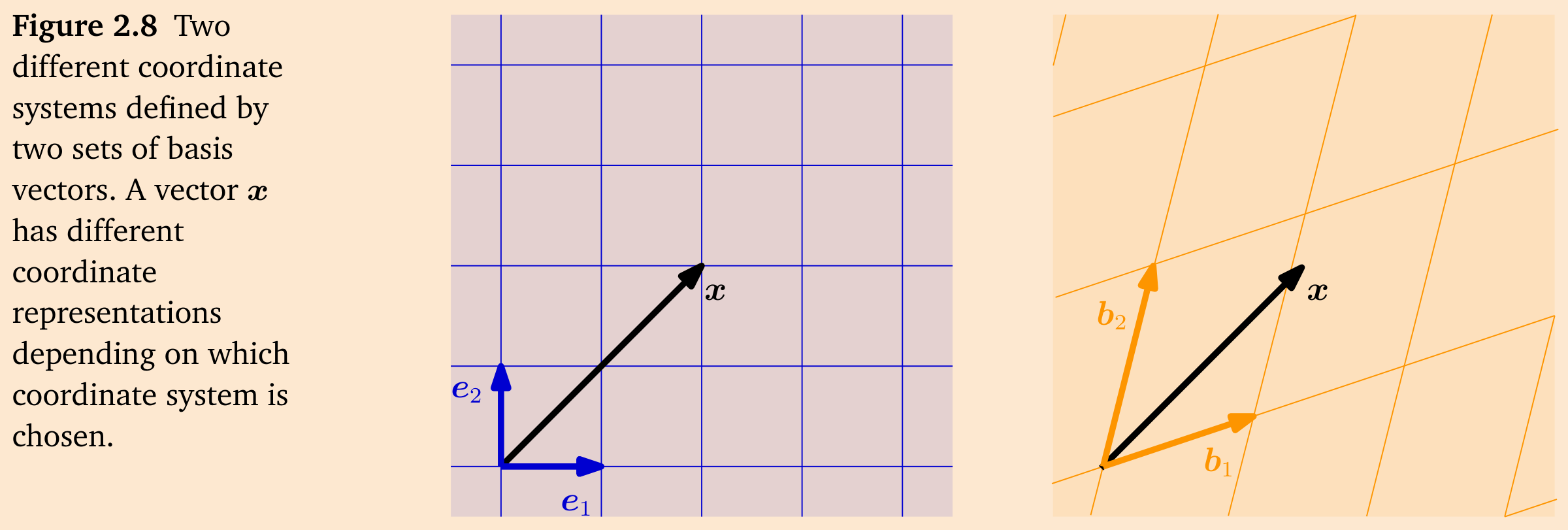
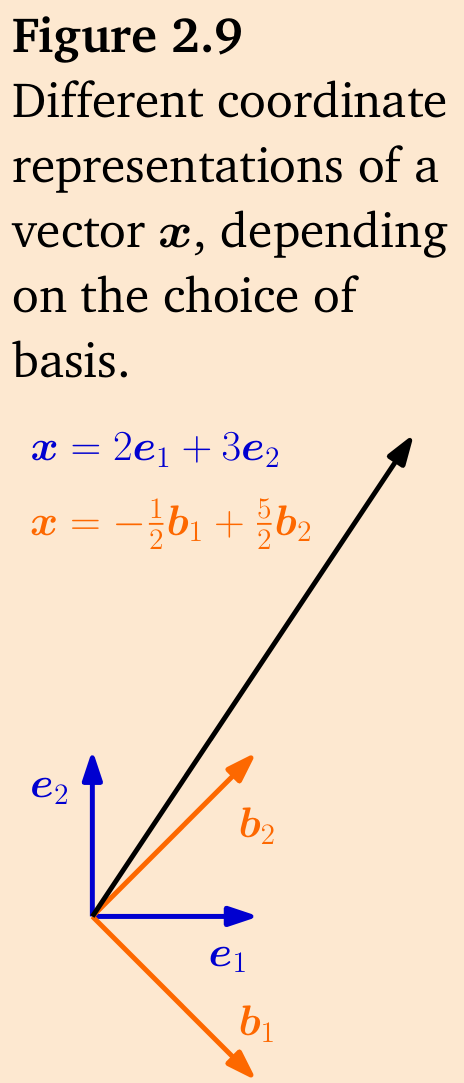
**例 2.20**

我们来看一个几何向量 $\mathit{x}\in {\mathbb{R}}^2$，其相对于 ${\mathbb{R}}^2$ 的标准基 $({\mathit{e}}_1,{\mathit{e}}_2)$ 的坐标为 $[2,3{]}^{\mathrm{\top }}$。这意味着，我们可以写作 $\mathit{x}=2{\mathit{e}}_1+3{\mathit{e}}_2$。然而，我们不必选择标准基来表示这个向量。如果我们使用基向量 ${\mathit{b}}_1=[1,-1{]}^{\mathrm{\top }}$ 和 ${\mathit{b}}_2=[1,1{]}^{\mathrm{\top }}$，我们将得到坐标 $\frac{1}{2}[-1,5{]}^{\mathrm{\top }}$ 来表示相对于 $({\mathit{b}}_1,{\mathit{b}}_2)$ 的相同向量（见图 2.9）。

---

备注。对于一个 $n$ 维向量空间 $V$ 和 $V$ 的一个有序基 $B$，映射 $\mathrm{\Phi }:{\mathbb{R}}^n\to V,\mathrm{\Phi }\left({\mathit{e}}_i\right)={\mathit{b}}_i,i=1,\dots ,n$ 是线性的（根据定理 2.17，是一个同构），其中 $({\mathit{e}}_1,\dots ,{\mathit{e}}_n)$ 是 ${\mathbb{R}}^n$ 的标准基。

现在我们已经准备好明确地建立矩阵与有限维向量空间之间的线性映射之间的联系。

定义 2.19（变换矩阵）。考虑向量空间 $V$ 和 $W$，它们分别有对应的（有序）基 $B=({\mathit{b}}_1,\dots ,{\mathit{b}}_n)$ 和 $C=({\mathit{c}}_1,\dots ,{\mathit{c}}_m)$。此外，我们考虑一个线性映射 $\mathrm{\Phi }:V\to W$。对于 $j\in \{1,\dots ,n\}$，

$$\begin{array}{}\text{(2.92)}& \mathrm{\Phi }\left({\mathit{b}}_j\right)={\alpha }_{1j}{\mathit{c}}_1+\cdots +{\alpha }_{mj}{\mathit{c}}_m=\sum _{i=1}^m{\alpha }_{ij}{\mathit{c}}_i\end{array}$$

是 $\mathrm{\Phi }\left({\mathit{b}}_j\right)$ 相对于 $C$ 的唯一表示。然后，我们称 $m\times n$ 矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$，其元素由下式给出

$$\begin{array}{}\text{(2.93)}& A_{\mathrm{\Phi }}(i,j)={\alpha }_{ij},\end{array}$$

为 $\mathrm{\Phi }$ 的变换矩阵（相对于 $V$ 的有序基 $B$ 和 $W$ 的有序基 $C$）。

$\mathrm{\Phi }\left({\mathit{b}}_j\right)$ 相对于 $W$ 的有序基 $C$ 的坐标是 ${\mathit{A}}_{\mathrm{\Phi }}$ 的第 $j$ 列。考虑（有限维）向量空间 $V,W$ 具有有序基 $B,C$ 和线性映射 $\mathrm{\Phi }:V\to W$ 及其变换矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$。如果 $\hat{\mathit{x}}$ 是 $\mathit{x}\in V$ 相对于 $B$ 的坐标向量，$\hat{\mathit{y}}$ 是 $\mathit{y}=\mathrm{\Phi }(\mathit{x})\in W$ 相对于 $C$ 的坐标向量，那么

$$\begin{array}{}\text{(2.94)}& \hat{\mathit{y}}={\mathit{A}}_{\mathrm{\Phi }}\hat{\mathit{x}}.\end{array}$$

这意味着变换矩阵可以用来将相对于 $V$ 中有序基的坐标映射为相对于 $W$ 中有序基的坐标。

---

**例 2.21（变换矩阵）**

考虑一个同态 $\mathrm{\Phi }:V\to W$ 以及 $V$ 的有序基 $B=({\mathit{b}}_1,\dots ,{\mathit{b}}_3)$ 和 $W$ 的有序基 $C=({\mathit{c}}_1,\dots ,{\mathit{c}}_4)$。给定

$$\begin{array}{}\text{(2.95)}& \begin{array}{rl}& \mathrm{\Phi }\left(b_1\right)=c_1-c_2+3c_3-c_4,\\ & \mathrm{\Phi }\left(b_2\right)=2c_1+c_2+7c_3+2c_4,\\ & \mathrm{\Phi }\left(b_3\right)=3c_2+c_3+4c_4,\end{array}\end{array}$$

相对于 $B$ 和 $C$ 的变换矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$ 满足 $\mathrm{\Phi }\left({\mathit{b}}_k\right)=\sum _{i=1}^4{\alpha }_{ik}{\mathit{c}}_i,k=1,\dots ,3$，其表示为

$$\begin{array}{}\text{(2.96)}& {\mathit{A}}_{\mathrm{\Phi }}=[{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3]=\left[\begin{array}{ccc}1& 2& 0\\ -1& 1& 3\\ 3& 7& 1\\ -1& 2& 4\end{array}\right],\end{array}$$

其中 ${\mathit{\alpha }}_j,j=1,2,3$，是 $\mathrm{\Phi }\left({\mathit{b}}_j\right)$ 相对于 $C$ 的坐标向量。

---

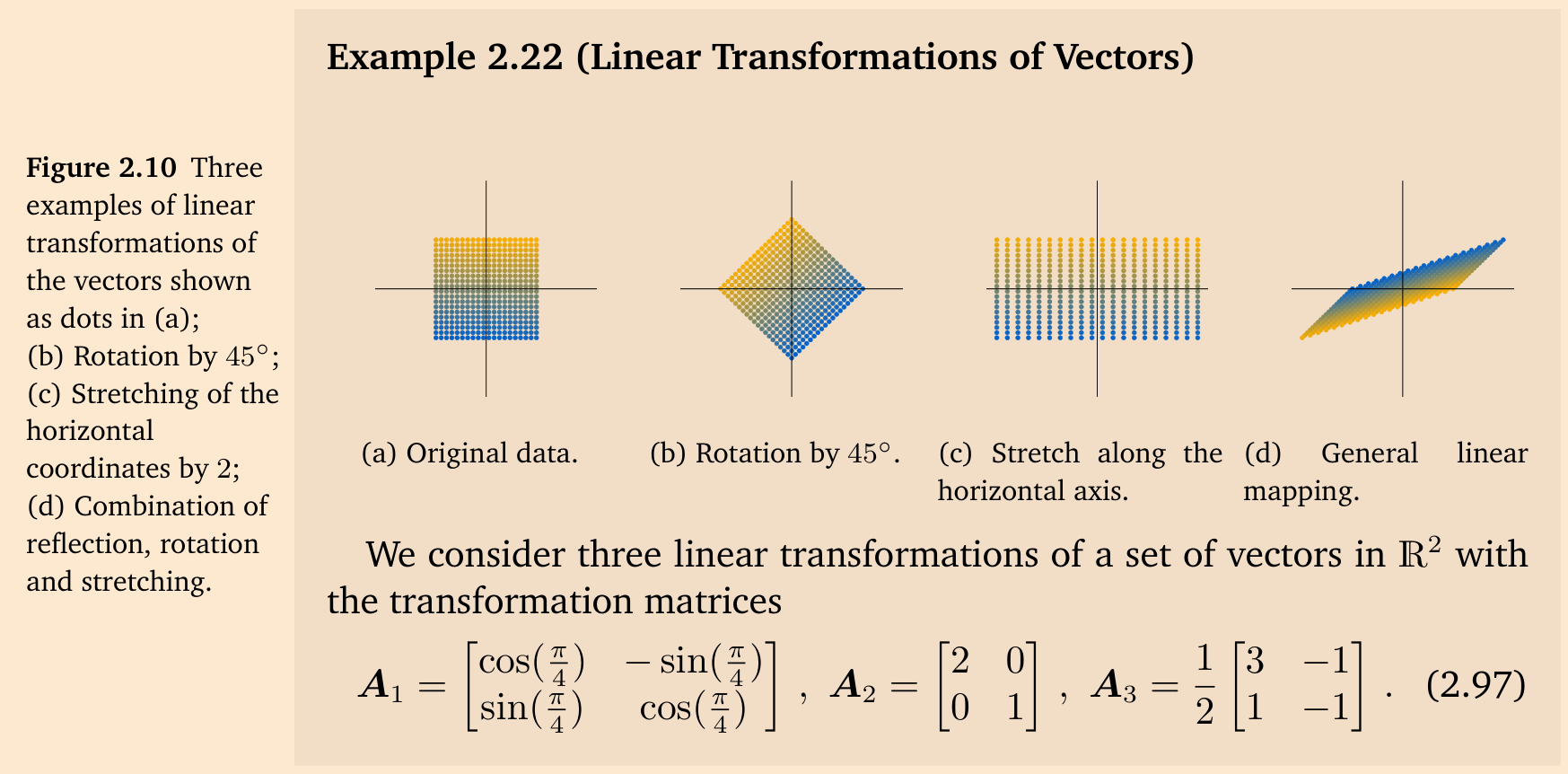
图 2.10 给出了一组向量的三个线性变换示例。图 2.10(a) 展示了 ${\mathbb{R}}^2$ 中的 400 个向量，每个向量由相应的 $(x_1,x_2)$ 坐标处的一个点表示。这些向量被排列在一个正方形中。当我们使用矩阵 ${\mathit{A}}_1$（在公式 2.97 中）对这些向量的每一个进行线性变换时，我们得到了图 2.10(b) 中的旋转正方形。如果我们应用由 ${\mathit{A}}_2$ 表示的线性映射，我们将得到图 2.10(c) 中的矩形，其中每个 $x_1$ 坐标被拉伸了 2 倍。图 2.10(d) 展示了使用 ${\mathit{A}}_3$ 进行线性变换后的原始正方形，它结合了反射、旋转和拉伸的效果。

2.7.2 基变换

在接下来的内容中，我们将更仔细地研究线性映射 $\mathrm{\Phi }:V\to W$ 的变换矩阵在我们改变 $V$ 和 $W$ 中的基时是如何变化的。考虑 $V$ 的两个有序基

$$\begin{array}{}\text{(2.98)}& B=({\mathit{b}}_1,\dots ,{\mathit{b}}_n),\tilde{B}=({\tilde{\mathit{b}}}_1,\dots ,{\tilde{\mathit{b}}}_n)\end{array}$$

和 $W$ 的两个有序基

$$\begin{array}{}\text{(2.99)}& C=({\mathit{c}}_1,\dots ,{\mathit{c}}_m),\tilde{C}=({\tilde{\mathit{c}}}_1,\dots ,{\tilde{\mathit{c}}}_m)\end{array}$$

此外，$A_{\mathrm{\Phi }}\in {\mathbb{R}}^{m\times n}$ 是相对于基 $B$ 和 $C$ 的线性映射 $\mathrm{\Phi }:V\to W$ 的变换矩阵，而 ${\tilde{\mathit{A}}}_{\mathrm{\Phi }}\in {\mathbb{R}}^{m\times n}$ 是相对于 $\tilde{B}$ 和 $\tilde{C}$ 的相应变换矩阵。接下来，我们将研究 $\mathit{A}$ 和 $\tilde{\mathit{A}}$ 是如何关联的，即如果我们选择从 $B,C$ 改变基到 $\tilde{B},\tilde{C}$，我们是否可以/如何将 ${\mathit{A}}_{\mathrm{\Phi }}$ 转换为 ${\tilde{A}}_{\mathrm{\Phi }}$。

备注。我们实际上得到了恒等映射 ${\mathrm{id}}_V$ 的不同坐标表示。在图 2.9 的上下文中，这意味着在不改变向量 $\mathit{x}$ 的情况下，将相对于 $({\mathit{e}}_1,{\mathit{e}}_2)$ 的坐标映射到相对于 $(b_1,b_2)$ 的坐标。通过改变基和相应地改变向量的表示，相对于这个新基的变换矩阵可以有一个特别简单的形式，这允许进行直接的计算。

---

**例 2.23（基变换）**

考虑一个相对于 ${\mathbb{R}}^2$ 中的标准基的变换矩阵

$$\begin{array}{}\text{(2.100)}& \mathit{A}=\left[\begin{array}{ll}2& 1\\ 1& 2\end{array}\right]\end{array}$$

如果我们定义一个新的基

$$\begin{array}{}\text{(2.101)}& B=(\left[\begin{array}{l}1\\ 1\end{array}\right],\left[\begin{array}{c}1\\ -1\end{array}\right])\end{array}$$

我们将获得一个对角变换矩阵

$$\begin{array}{}\text{(2.102)}& \tilde{\mathit{A}}=\left[\begin{array}{ll}3& 0\\ 0& 1\end{array}\right]\end{array}$$

相对于基 $B$，其比 $\mathit{A}$ 更容易处理。

---

接下来，我们将研究将一个基下的坐标向量变换为另一个基下的坐标向量的映射。我们将首先陈述主要结果，然后提供解释。

定理 2.20（基变换）。对于线性映射 $\mathrm{\Phi }:V\to W$，$V$ 的有序基

$$\begin{array}{}\text{(2.103)}& B=({\mathit{b}}_1,\dots ,{\mathit{b}}_n),\tilde{B}=({\tilde{\mathit{b}}}_1,\dots ,{\tilde{\mathit{b}}}_n)\end{array}$$

和 $W$ 的有序基

$$\begin{array}{}\text{(2.104)}& C=({\mathit{c}}_1,\dots ,{\mathit{c}}_m),\tilde{C}=({\tilde{\mathit{c}}}_1,\dots ,{\tilde{\mathit{c}}}_m)\end{array}$$

以及相对于基 $B$ 和 $C$ 的 $\mathrm{\Phi }$ 的变换矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$，相对于基 $\tilde{B}$ 和 $\tilde{C}$ 的相应变换矩阵 ${\tilde{A}}_{\mathrm{\Phi }}$ 由下式给出：

$$\begin{array}{}\text{(2.105)}& {\tilde{A}}_{\mathrm{\Phi }}={\mathit{T}}^{-1}{\mathit{A}}_{\mathrm{\Phi }}S\end{array}$$

这里，$S\in {\mathbb{R}}^{n\times n}$ 是将相对于 $\tilde{B}$ 的坐标映射到相对于 $B$ 的坐标的 ${\mathrm{id}}_V$ 的变换矩阵，而 $\mathit{T}\in {\mathbb{R}}^{m\times m}$ 是将相对于 $\tilde{C}$ 的坐标映射到相对于 $C$ 的坐标的 ${\mathrm{id}}_W$ 的变换矩阵。

证明 遵循 Drumm 和 Weil (2001) 的方法，我们可以将 $V$ 的新基 $\tilde{B}$ 的向量表示为基 $B$ 的基向量的线性组合，使得

$$\begin{array}{}\text{(2.106)}& {\tilde{\mathit{b}}}_j=s_{1j}{\mathit{b}}_1+\cdots +s_{nj}{\mathit{b}}_n=\sum _{i=1}^n{s}_{ij}{\mathit{b}}_i,j=1,\dots ,n.\end{array}$$

同样，我们将 $W$ 的新基向量 $\tilde{C}$ 表示为基 $C$ 的基向量的线性组合，得到

$$\begin{array}{}\text{(2.107)}& {\tilde{\mathit{c}}}_k=t_{1k}{\mathit{c}}_1+\cdots +t_{mk}{\mathit{c}}_m=\sum _{l=1}^m{t}_{lk}{\mathit{c}}_l,k=1,\dots ,m.\end{array}$$

我们定义 $\mathit{S}=(s_{ij})\in {\mathbb{R}}^{n\times n}$ 为变换矩阵，它将相对于 $\tilde{B}$ 的坐标映射到相对于 $B$ 的坐标，定义 $\mathit{T}=(t_{lk})\in {\mathbb{R}}^{m\times m}$ 为变换矩阵，它将相对于 $\tilde{C}$ 的坐标映射到相对于 $C$ 的坐标。特别地，$\mathit{S}$ 的第 $j$ 列是 ${\tilde{\mathit{b}}}_j$ 相对于 $B$ 的坐标表示，$\mathit{T}$ 的第 $k$ 列是 ${\tilde{\mathit{c}}}_k$ 相对于 $C$ 的坐标表示。注意，$\mathit{S}$ 和 $\mathit{T}$ 都是正则矩阵。

我们将从两个角度来观察 $\mathrm{\Phi }({\tilde{\mathit{b}}}_j)$。首先，应用映射 $\mathrm{\Phi }$，我们得到对于所有的 $j=1,\dots ,n$：

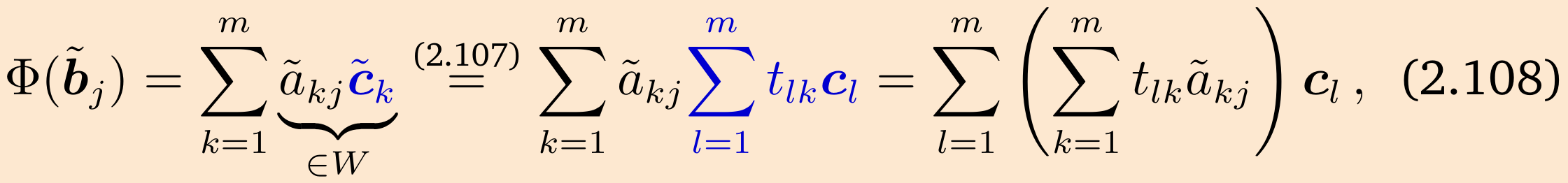
其中我们首先将新的基向量 ${\tilde{\mathit{c}}}_k\in W$ 表示为基向量 ${\mathit{c}}_l\in W$ 的线性组合，然后交换求和的顺序。

或者，当我们将 ${\tilde{\mathit{b}}}_j\in V$ 表示为 ${\mathit{b}}_j\in V$ 的线性组合时，我们得到

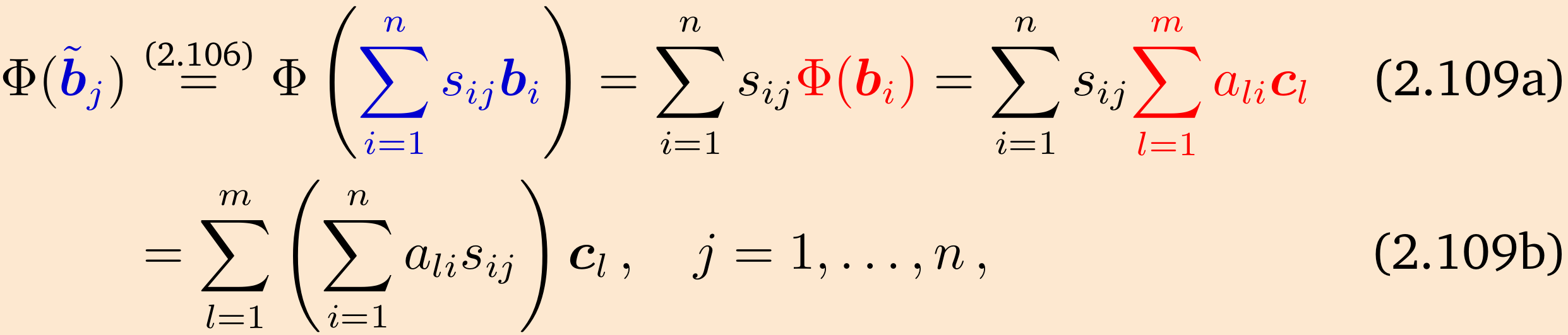
在这里，我们利用了 $\mathrm{\Phi }$ 的线性特性。比较公式 (2.108) 和 (2.109b)，可以得出对于所有的 $j=1,\dots ,n$ 和 $l=1,\dots ,m$ 有

$$\begin{array}{}\text{(2.110)}& \sum _{k=1}^m{t}_{lk}{\tilde{a}}_{kj}=\sum _{i=1}^n{a}_{li}{s}_{ij}\end{array}$$

因此，

$$\begin{array}{}\text{(2.111)}& \mathit{T}{\tilde{\mathit{A}}}_{\mathrm{\Phi }}={\mathit{A}}_{\mathrm{\Phi }}\mathit{S}\in {\mathbb{R}}^{m\times n},\end{array}$$

这样就有

$$\begin{array}{}\text{(2.112)}& {\tilde{A}}_{\mathrm{\Phi }}=T^{-1}{A}_{\mathrm{\Phi }}S,\end{array}$$

这证明了定理 2.20。

定理 2.20 告诉我们，当 $V$ 中的基（$B$ 被 $\tilde{B}$ 取代）和 $W$ 中的基（$C$ 被 $\tilde{C}$ 取代）发生变化时，线性映射 $\mathrm{\Phi }:V\to W$ 的变换矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$ 被替换为等效矩阵 ${\tilde{\mathit{A}}}_{\mathrm{\Phi }}$，其关系为：

$$\begin{array}{}\text{(2.113)}& {\tilde{A}}_{\mathrm{\Phi }}=T^{-1}{A}_{\mathrm{\Phi }}S.\end{array}$$

图 2.11 说明了这种关系：考虑一个同态映射 $\mathrm{\Phi }:V\to W$ 及 $V$ 的有序基 $B,\tilde{B}$ 和 $W$ 的有序基 $C,\tilde{C}$。映射 ${\mathrm{\Phi }}_{CB}$ 是 $\mathrm{\Phi }$ 的一个实例，将 $B$ 的基向量映射到 $C$ 的基向量的线性组合。假设我们知道 ${\mathrm{\Phi }}_{CB}$ 的变换矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$，对应于有序基 $B,C$。当我们在 $V$ 中从 $B$ 到 $\tilde{B}$ 和在 $W$ 中从 $C$ 到 $\tilde{C}$ 进行基变换时，我们可以确定相应的变换矩阵 ${\tilde{\mathit{A}}}_{\mathrm{\Phi }}$ 如下

• 首先，我们找到线性映射 ${\mathrm{\Psi }}_{B\tilde{B}}:V\to V$ 的矩阵表示，该映射将相对于新基 $\tilde{B}$ 的坐标映射到（唯一的）相对于“旧”基 $B$ 的坐标（在 $V$ 中）。
• 然后，我们使用 ${\mathrm{\Phi }}_{CB}:V\to W$ 的变换矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$ 将这些坐标映射到 $W$ 中相对于 $C$ 的坐标。
• 最后，我们使用线性映射 ${\mathrm{\Xi }}_{\tilde{C}C}:W\to W$ 将相对于 $C$ 的坐标映射到相对于 $\tilde{C}$ 的坐标。因此，我们可以将线性映射 ${\mathrm{\Phi }}_{\tilde{C}\tilde{B}}$ 表示为涉及“旧”基的线性映射的组合：

$$\begin{array}{}\text{(2.114)}& {\mathrm{\Phi }}_{\tilde{C}\tilde{B}}={\mathrm{\Xi }}_{\tilde{C}C}\circ {\mathrm{\Phi }}_{CB}\circ {\mathrm{\Psi }}_{B\tilde{B}}={\mathrm{\Xi }}_{C\tilde{C}}^{-1}\circ {\mathrm{\Phi }}_{CB}\circ {\mathrm{\Psi }}_{B\tilde{B}}.\end{array}$$

具体来说，我们使用 ${\mathrm{\Psi }}_{B\tilde{B}}={\mathrm{id}}_V$ 和 ${\mathrm{\Xi }}_{C\tilde{C}}={\mathrm{id}}_W$，即将向量映射到其自身的恒等映射，但相对于不同的基。

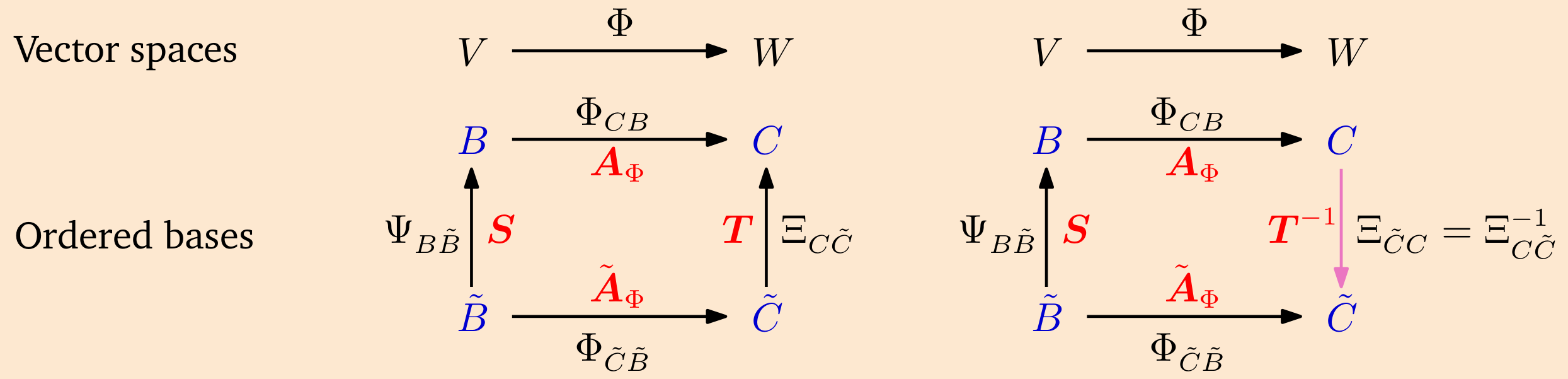
图 2.11 对于同态映射 $\mathrm{\Phi }:V\to W$ 以及 $V$ 的有序基 $B,\tilde{B}$ 和 $W$ 的有序基 $C,\tilde{C}$（用蓝色标记），我们可以将相对于基 $\tilde{B},\tilde{C}$ 的映射 ${\mathrm{\Phi }}_{\tilde{C}\tilde{B}}$ 等效地表示为同态映射 ${\mathrm{\Phi }}_{\tilde{C}\tilde{B}}=$ ${\mathrm{\Xi }}_{\tilde{C}C}\circ {\mathrm{\Phi }}_{CB}\circ {\mathrm{\Psi }}_{B\tilde{B}}$ 的组合，其下标表示了相应的基。相应的变换矩阵用红色标出。

定义 2.21（等价）。如果存在正则矩阵 $S\in {\mathbb{R}}^{n\times n}$ 和 $\mathit{T}\in {\mathbb{R}}^{m\times m}$，使得 $\tilde{A}=T^{-1}AS$，那么两个矩阵 $\mathit{A},\tilde{A}\in {\mathbb{R}}^{m\times n}$ 是等价的。

定义 2.22（相似）。如果存在正则矩阵 $S\in {\mathbb{R}}^{n\times n}$ 使得 $\tilde{A}={\mathit{S}}^{-1}\mathit{A}\mathit{S}$，那么两个矩阵 $\mathit{A},\tilde{A}\in {\mathbb{R}}^{n\times n}$ 是相似的。

备注。相似矩阵总是等价的。然而，等价矩阵不一定是相似的。

备注。考虑向量空间 $V,W,X$。从定理 2.17 后的备注中我们已经知道，对于线性映射 $\mathrm{\Phi }:V\to W$ 和 $\mathrm{\Psi }:W\to X$，映射 $\mathrm{\Psi }\circ \mathrm{\Phi }:V\to X$ 也是线性的。对于相应映射的变换矩阵 ${\mathit{A}}_{\mathrm{\Phi }}$ 和 ${\mathit{A}}_{\mathrm{\Psi }}$，整体变换矩阵为 ${\mathit{A}}_{\mathrm{\Psi }\circ \mathrm{\Phi }}={\mathit{A}}_{\mathrm{\Psi }}{\mathit{A}}_{\mathrm{\Phi }}$。

根据这一说明，我们可以从组合线性映射的角度来看待基变换：

• ${\mathit{A}}_{\mathrm{\Phi }}$ 是相对于基 $B,C$ 的线性映射 ${\mathrm{\Phi }}_{CB}:V\to W$ 的变换矩阵。
• ${\tilde{A}}_{\mathrm{\Phi }}$ 是相对于基 $\tilde{B},\tilde{C}$ 的线性映射 ${\mathrm{\Phi }}_{\tilde{C}\tilde{B}}:V\to W$ 的变换矩阵。
• $S$ 是相对于基 $B,\tilde{B}$ 的线性映射 ${\mathrm{\Psi }}_{B\tilde{B}}:V\to V$（自同构）的变换矩阵，它用 $B$ 来表示 $\tilde{B}$。通常，$\mathrm{\Psi }={\mathrm{id}}_V$ 是 $V$ 中的恒等映射。
• $\mathit{T}$ 是相对于基 $C,\tilde{C}$ 的线性映射 ${\mathrm{\Xi }}_{C\tilde{C}}:W\to W$（自同构）的变换矩阵，它用 $C$ 来表示 $\tilde{C}$。通常，$\mathrm{\Xi }={\mathrm{id}}_W$ 是 $W$ 中的恒等映射。

如果我们（非正式地）只根据基来写下这些变换，那么 ${\mathit{A}}_{\mathrm{\Phi }}:B\to C,{\tilde{\mathit{A}}}_{\mathrm{\Phi }}:\tilde{B}\to \tilde{C},\mathit{S}:\tilde{B}\to B,\mathit{T}:\tilde{C}\to C$ 和 ${\mathit{T}}^{-1}:C\to \tilde{C}$，并且

$$\begin{array}{}\text{(2.115)}& \tilde{B}\to \tilde{C}& =\tilde{B}\to B\to C\to \tilde{C}\text{(2.116)}& {\tilde{\mathit{A}}}_{\mathrm{\Phi }}& ={\mathit{T}}^{-1}{\mathit{A}}_{\mathrm{\Phi }}\mathit{S}.\end{array}$$

注意，公式 (2.116) 中的执行顺序是从右到左的，因为向量是在右侧进行相乘的，所以 $\mathit{x}\mapsto \mathit{S}\mathit{x}\mapsto {\mathit{A}}_{\mathrm{\Phi }}(\mathit{S}\mathit{x})\mapsto T^{-1}(A_{\mathrm{\Phi }}(Sx))={\tilde{\mathit{A}}}_{\mathrm{\Phi }}x$。

---

**示例 2.24（基变换）**

考虑一个线性映射 $\mathrm{\Phi }:{\mathbb{R}}^3\to {\mathbb{R}}^4$，其变换矩阵为

$$\begin{array}{}\text{(2.117)}& {\mathit{A}}_{\mathrm{\Phi }}=\left[\begin{array}{ccc}1& 2& 0\\ -1& 1& 3\\ 3& 7& 1\\ -1& 2& 4\end{array}\right]\end{array}$$

相对于标准基

$$\begin{array}{}\text{(2.118)}& B=(\left[\begin{array}{l}1\\ 0\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 1\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 0\\ 1\end{array}\right]),C=(\left[\begin{array}{l}1\\ 0\\ 0\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 1\\ 0\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 0\\ 1\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 0\\ 0\\ 1\end{array}\right]).\end{array}$$

我们要找出相对于新基

$$\begin{array}{}\text{(2.119)}& \tilde{B}=(\left[\begin{array}{l}1\\ 1\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 1\\ 1\end{array}\right],\left[\begin{array}{l}1\\ 0\\ 1\end{array}\right])\in {\mathbb{R}}^3,\tilde{C}=(\left[\begin{array}{l}1\\ 1\\ 0\\ 0\end{array}\right],\left[\begin{array}{l}1\\ 0\\ 1\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 1\\ 1\\ 0\end{array}\right],\left[\begin{array}{l}1\\ 0\\ 0\\ 1\end{array}\right]).\end{array}$$

下的变换矩阵 ${\tilde{\mathit{A}}}_{\mathrm{\Phi }}$。

则

$$\begin{array}{}\text{(2.120)}& \mathit{S}=\left[\begin{array}{lll}1& 0& 1\\ 1& 1& 0\\ 0& 1& 1\end{array}\right],\mathit{T}=\left[\begin{array}{llll}1& 1& 0& 1\\ 1& 0& 1& 0\\ 0& 1& 1& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

其中 $S$ 的第 $i$ 列是 ${\tilde{\mathit{b}}}_i$ 相对于基 $B$ 的坐标表示。由于 $B$ 是标准基，坐标表示很容易找到。对于一般基 $B$，我们需要解线性方程组以找到 ${\lambda }_i$ 使得 $\sum _{i=1}^3{\lambda }_i{\mathit{b}}_i={\tilde{\mathit{b}}}_j,j=1,\dots ,3$。类似地，$T$ 的第 $j$ 列是 ${\tilde{c}}_j$ 相对于基 $C$ 的坐标表示。

因此，我们得到

$$\begin{array}{}\text{(2.121a)}& {\tilde{\mathit{A}}}_{\mathrm{\Phi }}& ={\mathit{T}}^{-1}{\mathit{A}}_{\mathrm{\Phi }}\mathit{S}=\frac{1}{2}\left[\begin{array}{cccc}1& 1& -1& -1\\ 1& -1& 1& -1\\ -1& 1& 1& 1\\ 0& 0& 0& 2\end{array}\right]\left[\begin{array}{ccc}3& 2& 1\\ 0& 4& 2\\ 10& 8& 4\\ 1& 6& 3\end{array}\right]\text{(2.121b)}& & =\left[\begin{array}{ccc}-4& -4& -2\\ 6& 0& 0\\ 4& 8& 4\\ 1& 6& 3\end{array}\right].\end{array}$$

---

在第4章中，我们将能够利用基变换的概念找到一个基，使得自同态的变换矩阵具有特别简单的（对角）形式。在第10章中，我们将研究一个数据压缩问题，并找到一个方便的基，我们可以将数据投影到这个基上，同时最小化压缩损失。

3.7.3 像和核

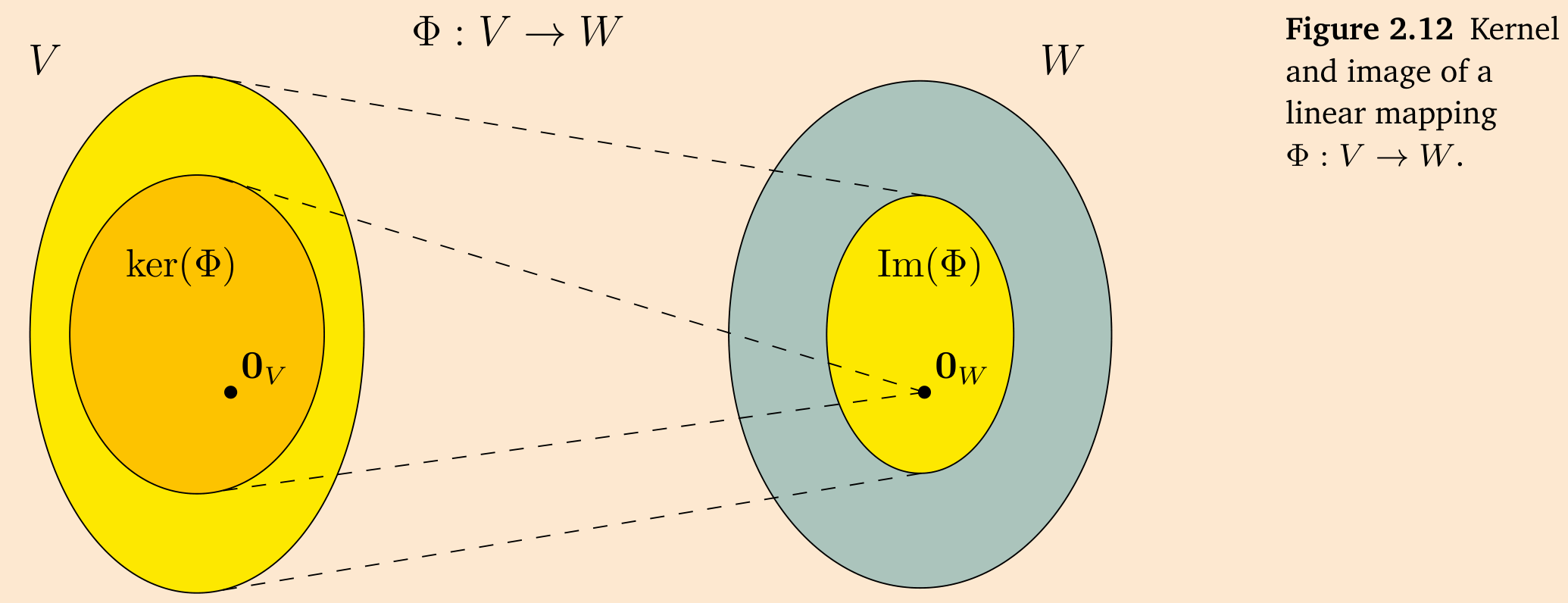
线性映射的像和核是具有某些重要性质的向量子空间。接下来，我们将更仔细地描述它们。

定义 2.23（像和核）。

对于 $\mathrm{\Phi }:V\to W$，我们定义 核/零空间

$$\ker (\mathrm{\Phi }):={\mathrm{\Phi }}^{-1}\left({\mathbf{0}}_W\right)=\{\mathit{v}\in V:\mathrm{\Phi }(\mathit{v})={\mathbf{0}}_W\}$$

和 像/值域

$$\mathrm{Im}(\mathrm{\Phi }):=\mathrm{\Phi }(V)=\{\mathit{w}\in W\mid \mathrm{\exists }\mathit{v}\in V:\mathrm{\Phi }(\mathit{v})=\mathit{w}\}$$

我们也分别称 $V$ 和 $W$ 为 $\mathrm{\Phi }$ 的定义域和值域。

直观上，核是 $\mathrm{\Phi }$ 映射到 $W$ 中的中性元素 ${\mathbf{0}}_W\in W$ 的向量集 $\mathit{v}\in V$。像是可以通过 $\mathrm{\Phi }$ 从 $V$ 中任何向量“到达”的向量 $\mathit{w}\in W$ 的集合。图 2.12 中给出了一个示意图。

备注。考虑一个线性映射 $\mathrm{\Phi }:V\to W$，其中 $V,W$ 是向量空间。

• $\mathrm{\Phi }\left({\mathbf{0}}_V\right)={\mathbf{0}}_W$ 总是成立，因此 ${\mathbf{0}}_V\in \ker (\mathrm{\Phi })$。特别是，零空间永远不会为空。
• $\mathrm{Im}(\mathrm{\Phi })\subseteq W$ 是 $W$ 的一个子空间，而 $\ker (\mathrm{\Phi })\subseteq V$ 是 $V$ 的一个子空间。
• 当且仅当 $\ker (\mathrm{\Phi })=\{\mathbf{0}\}$ 时，$\mathrm{\Phi }$ 是单射（injective）（一一对应）。

注释（零空间和列空间）。我们考虑 $\mathit{A}\in {\mathbb{R}}^{m\times n}$ 和一个线性映射 $\mathrm{\Phi }:{\mathbb{R}}^n\to {\mathbb{R}}^m,\mathit{x}\mapsto \mathit{A}\mathit{x}$。

• 对于 $\mathit{A}=[{\mathit{a}}_1,\dots ,{\mathit{a}}_n]$，其中 ${\mathit{a}}_i$ 是 $\mathit{A}$ 的列，我们得到

$$\begin{array}{}\text{(2.124a)}& \mathrm{Im}(\mathrm{\Phi })& =\{\mathit{A}\mathit{x}:\mathit{x}\in {\mathbb{R}}^n\}=\{\sum _{i=1}^n{x}_i{\mathit{a}}_i:x_1,\dots ,x_n\in \mathbb{R}\}\text{(2.124b)}& & =\mathrm{span}[{\mathit{a}}_1,\dots ,{\mathit{a}}_n]\subseteq {\mathbb{R}}^m\end{array}$$

即，像是 $\mathit{A}$ 列的张成空间，也称为 列空间。因此，列空间（像）是 ${\mathbb{R}}^m$ 的一个子空间，其中 $m$ 是矩阵的“高度”。

• $\mathrm{rk}(\mathit{A})=\dim (\mathrm{Im}(\mathrm{\Phi }))$。
• 核/零空间 $\ker (\mathrm{\Phi })$ 是齐次线性方程组（homogeneous system of linear equations） $\mathit{A}\mathit{x}=\mathbf{0}$ 的通解，并且包含了所有可能的 ${\mathbb{R}}^n$ 中的元素的线性组合，它们产生 $\mathbf{0}\in {\mathbb{R}}^m$。
• 核是 ${\mathbb{R}}^n$ 的一个子空间，其中 $n$ 是矩阵的“宽度”。
• 核关注列之间的关系，我们可以用它来确定是否/如何将一列表示为其他列的线性组合。

---

**示例 2.25（线性映射的像和核）**

映射

$$\begin{array}{}\text{(2.125a)}& \mathrm{\Phi }:{\mathbb{R}}^4\to {\mathbb{R}}^2,\left[\begin{array}{l}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]& \mapsto \left[\begin{array}{cccc}1& 2& -1& 0\\ 1& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]=\left[\begin{array}{c}{x}_1+2x_2-x_3\\ x_1+x_4\end{array}\right]\text{(2.125b)}& & =x_1\left[\begin{array}{c}1\\ 1\end{array}\right]+x_2\left[\begin{array}{c}2\\ 0\end{array}\right]+x_3\left[\begin{array}{c}-1\\ 0\end{array}\right]+x_4\left[\begin{array}{c}0\\ 1\end{array}\right]\end{array}$$

是线性的。为了确定 $\mathrm{Im}(\mathrm{\Phi })$，我们可以取变换矩阵列的张成空间，得到

$$\begin{array}{}\text{(2.126)}& \mathrm{Im}(\mathrm{\Phi })=\mathrm{span}[\left[\begin{array}{l}1\\ 1\end{array}\right],\left[\begin{array}{l}2\\ 0\end{array}\right],\left[\begin{array}{c}-1\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 1\end{array}\right]]\end{array}$$

为了计算 $\mathrm{\Phi }$ 的核（零空间），我们需要解 $\mathit{A}\mathit{x}=\mathbf{0}$，即需要解一个齐次方程组。为此，我们使用高斯消元法将 $\mathit{A}$ 转换为简化行最简形式：

$$\begin{array}{}\text{(2.127)}& \left[\begin{array}{cccc}1& 2& -1& 0\\ 1& 0& 0& 1\end{array}\right]⇝\cdots ⇝\left[\begin{array}{cccc}1& 0& 0& 1\\ 0& 1& -\frac{1}{2}& -\frac{1}{2}\end{array}\right].\end{array}$$

这个矩阵是简化行最简形式，我们可以使用 Minus 1 Trick 计算核的一个基（参见第 2.3.3 节）。或者，我们可以将非主元列（第 3 列和第 4 列）表示为主元列（第 1 列和第 2 列）的线性组合。第三列 ${\mathit{a}}_3$ 等于 $-\frac{1}{2}$ 倍的第二列 ${\mathit{a}}_2$。因此，$\mathbf{0}={\mathit{a}}_3+\frac{1}{2}{\mathit{a}}_2$。同样地，我们看到 ${\mathit{a}}_4={\mathit{a}}_1-\frac{1}{2}{\mathit{a}}_2$，因此 $\mathbf{0}={\mathit{a}}_1-\frac{1}{2}{\mathit{a}}_2-{\mathit{a}}_4$。总的来说，这给出了核（零空间）为

$$\begin{array}{}\text{(2.128)}& \ker (\mathrm{\Phi })=\mathrm{span}[\left[\begin{array}{l}0\\ \frac{1}{2}\\ 1\\ 0\end{array}\right],\left[\begin{array}{c}-1\\ \frac{1}{2}\\ 0\\ 1\end{array}\right]]\end{array}$$

---

定理 2.24（秩-零化度定理）。对于 向量空间 $V$ 和 $W$ 以及 线性映射 $\mathrm{\Phi }:V\to W$，有

$$\begin{array}{}\text{(2.129)}& \dim (\ker (\mathrm{\Phi }))+\dim (\mathrm{Im}(\mathrm{\Phi }))=\dim (V).\end{array}$$

秩-零化度定理也被称为线性映射的基本定理（Axler, 2015, 定理 3.22）。以下是定理 2.24 的直接推论：

• 如果 $\dim (\mathrm{Im}(\mathrm{\Phi }))<\dim (V)$，则 $\ker (\mathrm{\Phi })$ 是非平凡的，即核包含除了 ${\mathbf{0}}_V$ 之外的元素，且 $\dim (\ker (\mathrm{\Phi }))⩾1$。
• 如果 ${\mathit{A}}_{\mathrm{\Phi }}$ 是相对于某个有序基的 $\mathrm{\Phi }$ 的变换矩阵，并且 $\dim (\mathrm{Im}(\mathrm{\Phi }))<\dim (V)$，则线性方程组 ${\mathit{A}}_{\mathrm{\Phi }}\mathit{x}=\mathbf{0}$ 有无穷多解。
• 如果 $\dim (V)=\dim (W)$，则以下三者等价：

$$\mathrm{\Phi }\text{ 是单射 }⟺\mathrm{\Phi }\text{ 是满射 }⟺\mathrm{\Phi }\text{ 是双射 }$$

因为 $\mathrm{Im}(\mathrm{\Phi })\subseteq W$。