python 之pulp 线性规划介绍及举例
pulp http://pythonhosted.org/PuLP/main/basic_python_coding.html
供水问题
1问题
供水公司有三个水库分别为A,B,C向四个小区甲乙丙丁供水,A和B向所有小区供水,C仅向甲乙丙供水,水库最大供水量(千吨)
|
水库 |
A |
B |
C |
|
最大供水量(千吨) |
50 |
60 |
50 |
小区用水情况为
|
小区 |
甲 |
乙 |
丙 |
丁 |
|
基本用水量(千吨) |
30 |
70 |
10 |
10 |
|
额外用水量(千吨) |
50 |
70 |
20 |
40 |
水库供水收入900元/千吨,支出费用为:其他费用450/千吨,引水管理费:
|
由水库到小区引水费用: 元/千吨 |
甲 |
乙 |
丙 |
丁 |
|
A |
160 |
130 |
220 |
170 |
|
B |
140 |
130 |
190 |
150 |
|
C |
190 |
200 |
230 |
|
问 如何分配水库供水量,公司才能获利最多。
2 解题思路
使引水管理费最小,则利润最高。
设:水库i向小区j的供水量为,总引水管理费为Z
目标函数为:z = 160.0*x11 + 130.0*x12 + 220.0*x13 + 170.0*x14 + 140.0*x21 + 130.0*x22 + 190.0*x23 + 150.0*x24 + 190.0*x31 + 200.0*x32 + 230.0*x33
求的值,使Z最小。
约束条件为:
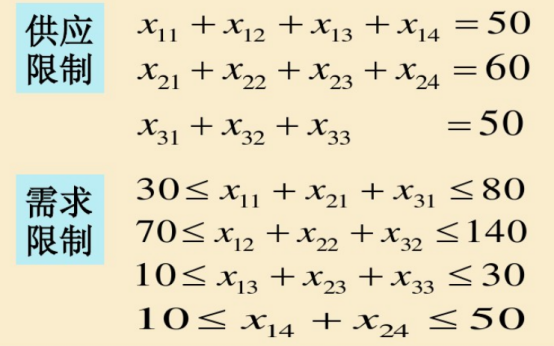
1 # coding=utf-8 2 3 from pulp import * 4 5 6 def get_re(): 7 pass 8 9 10 def getresult(c, con): 11 12 # 设置对象 13 prob = LpProblem('myPro', LpMinimize) 14 # 设置三个变量,并设置变量最小取值 15 16 x11 = LpVariable("x11", lowBound=0) 17 x12 = LpVariable("x12", lowBound=0) 18 x13 = LpVariable("x13", lowBound=0) 19 x14 = LpVariable("x14", lowBound=0) 20 x21 = LpVariable("x21", lowBound=0) 21 x22 = LpVariable("x22", lowBound=0) 22 x23 = LpVariable("x23", lowBound=0) 23 x24 = LpVariable("x24", lowBound=0) 24 x31 = LpVariable("x31", lowBound=0) 25 x32 = LpVariable("x32", lowBound=0) 26 x33 = LpVariable("x33", lowBound=0) 27 28 X = [x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33] 29 30 #c = [160, 130, 220, 170, 140, 130, 190, 150, 190, 200, 230] 31 32 33 34 35 36 37 # 目标函数 38 z = 0 39 for i in range(len(X)): 40 z += X[i]*c[i] 41 #print(z) 42 prob += z 43 44 # 载入约束变量 45 prob += x11+x12+x13+x14 == con[0]# 约束条件1 46 prob += x21+x22+x23+x24 == con[1] 47 prob += x31+x32+x33 == con[2] 48 49 prob += x11+x21+x31 <= con[3] 50 prob += x11+x21+x31 >= con[4] 51 52 prob += x12 + x22 + x32 <= con[5] 53 prob += x12 + x22 + x32 >= con[6] 54 55 prob += x13 + x23 + x33 <= con[7] 56 prob += x13 + x23 + x33 >= con[8] 57 prob += x14 + x24 <= con[9] 58 prob += x14 + x24 >= con[10] 59 60 # 求解 61 62 status = prob.solve() 63 64 print(status) 65 print(LpStatus[status]) 66 print(value(prob.objective)) # 计算结果 67 68 69 # 显示结果 70 # for i in prob.variables(): 71 # print(i.name + "=" + str(i.varValue)) 72 for i in prob.variables(): 73 print(i.varValue) 74 75 76 if __name__ == '__main__': 77 c = [160, 130, 220, 170, 140, 130, 190, 150, 190, 200, 230] 78 con = [50, 60, 50, 80, 30, 140, 70, 30,10, 50, 10] 79 getresult(mubiao, yueshu)
输出结果:
1
Optimal
24400.0
0.0
50.0
0.0
0.0
0.0
50.0
0.0
10.0
40.0
0.0
10.0




