[NLP] 相对位置编码(一) Relative Position Representatitons (RPR) - Transformer

对于Transformer模型的positional encoding，最初在Attention is all you need的文章中提出的是进行绝对位置编码，之后Shaw在2018年的文章中提出了相对位置编码，就是本篇blog所介绍的算法RPR；2019年的Transformer-XL针对其segment的特定，引入了全局偏置信息，改进了相对位置编码的算法，在相对位置编码(二)的blog中介绍。 

本文参考链接：

1. Self-Attention with Relative Position Representations (Shaw et al.2018): https://arxiv.org/pdf/1803.02155.pdf 

2. Attention is all you need (Vaswani et al.2017): https://arxiv.org/pdf/1706.03762.pdf

3. How Self-Attention with Relative Position Representations works: https://medium.com/@_init_/how-self-attention-with-relative-position-representations-works-28173b8c245a

4. [NLP] 相对位置编码(二) Relative Positional Encodings - Transformer-XL: https://www.cnblogs.com/shiyublog/p/11236212.html

Motivation

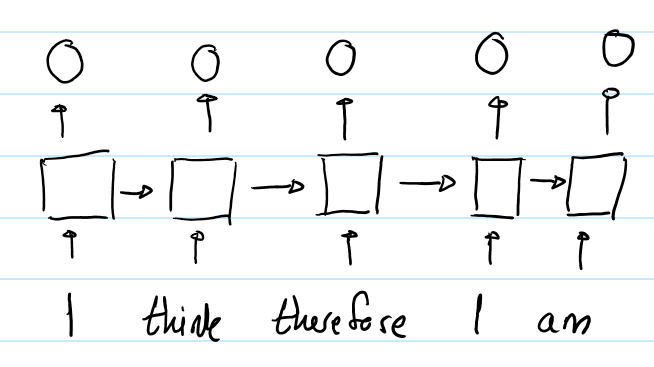
RNN中，第一个"I"与第二个"I"的输出表征不同，因为用于生成这两个单词的hidden states是不同的。对于第一个"I"，其hidden state是初始化的状态；对于第二个"I"，其hidden state是编码了"I think therefore"的hidden state。所以RNN的hidden state 保证了在同一个输入序列中，不同位置的同样的单词的output representation是不同的。

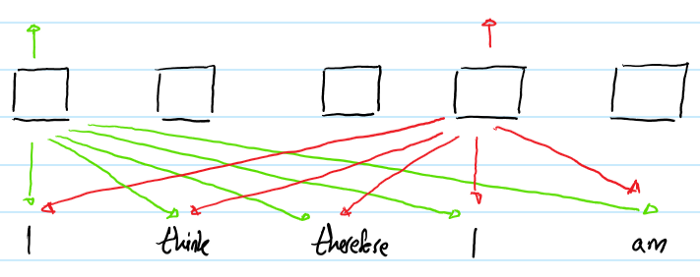
在self-attention中，第一个"I"与第二个"I"的输出将完全相同。因为它们用于产生输出的“input”是完全相同的。即在同一个输入序列中，不同位置的相同的单词的output representation完全相同，这样就不能提现单词之间的时序关系。--所以要对单词的时序位置进行编码表征。

概述

作者提出了在Transformer模型中加入可训练的embedding编码，使得output representatino可以表征inputs的时序信息。这些embedding vectors是 在计算输入序列中的任意两个单词$i, j$ 之间的attention weight 和 value时被加入到其中。embedding vector用于表示单词$i,j$之间的距离(即为间隔的单词数),所以命名为"相对位置表征" (Relative Position Representation) (RPR)

比如一个长度为5的序列，需要学习9个embeddings。(1个表示当前单词，4个表示其左边的单词，4个表示其右边的单词。)

以下例子展示了这些embeddings的用法:

1) 

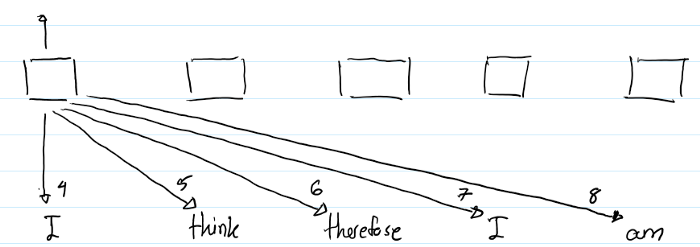
以上图示显示了计算第一个"I"的output representation的过程。箭头下面的数字显示了计算attention时用到的哪个RPRs.(比如，本示例是求第一个“I”的输出，需要用第一个“I”,记为''I_1'，与sequence中每一个单词两两做self-attention运算。'I_1' with 'I_1'用到 index = 4 的RPR，“I_1”with 'think'用到index = 5 的RPR--因为是右边第一个， 'I_1' with 'therefore' 用到index = 6的RPR--因为是右边第二个... )

2)  

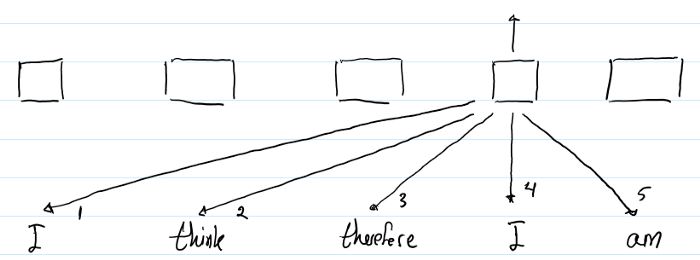
与(1)同理。

符号含义 

两点需要注意：

1. 有2个RPR的表征。需要在计算$z_i$和$e_{ij}$时分别引入对应的RPR的embedding。计算$z_i$时对应的RPR vector 是$a_{ij}^V$, 计算$e_{ij}时引入的RPR vector$是$a_{ij}^K$. 不同于在做multi-head attention时引入的线性映射矩阵W——对于每个head都不同；这个RPR embedding 在同一层的attention heads之间共享，但是在不同层的RPR可能不同。

2. 最大单词数被clipped在一个绝对的值k以内。向左k个, 再左边均为0， 向右k个，再右边均为k, 所表示的index范围： 2k + 1. 

eg. 10 words, k = 3, RPR embedding lookup table 

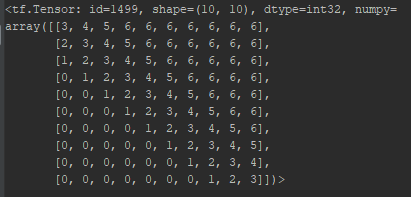
设置k值截断的意义：

1. 作者假设精确的相对位置编码在超出了一定距离之后是没有必要的

2. 截断最大距离使得模型的泛化效果好，可以更好的Generalize到没有在训练阶段出现过的序列长度上。

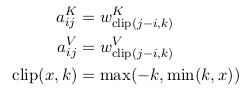
之后，将分别学习key, value的相对位置表征。

$$w^{K} = (w_{-k}^K, ..., w_{k} ^K), w^{V} = (w_{-k}^V, ..., w_{k} ^V)$$

其中$w_i^K, w_i^V \in \mathbb{R}^{d_a}$.

实现

1. 若不使用RPR, 计算$z_i$的过程：

 

2. 若使用RPR，计算$z_i$的过程：

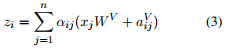
(3) 表示在计算word i 的output representation时，对于word j的value vector进行了修改，加上了word i, j 之间的相对位置编码。

(4) 在计算query(i), key(j)的点积时，对key vector进行了修改，加上了word i, j 之间的相对位置编码。

这里用加法引入RPR的信息，是一种高效的实现方式。

高效实现

不加RPR时，Transformer计算$e_{ij}$使用了 batch_size * h 个并行的矩阵乘法运算。

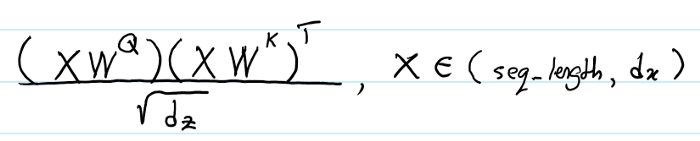
其中的x是给定input sequence后的(row-wise)

将(4) 式写为以下形式：

(1) 首先看第一项，$$x_iW^Q(x_jW^K)^T$$

首先看对于一个batch,的一个head， 其中$x_i$的shape是(seq_length, dx)，现在假设seq_length = 1,来简化推导过程。假设$W^Q, W^K$的shape均为(dx, dz)，那么第一项运算后的shape为：[(1 * dx) * (dx, dz)] * [(dz, dx) * (dx, 1)] = (1, 1)，

这是对于一个batch,一个head, seq_length = 1的情况，那么扩充到真实的情况，其shape 为： (batch_size, h, seq_length, seq_length)

所以我们的目标是产生另一个有相同shape的tensor，其内容是word i 与关于Wordi, j 的RPR的embedding的点积。

(2) A.shape: (seq_length, seq_length, d_a)，

$transpose \rightarrow A^T.shape: $(seq_length, d_a, seq_length)

(3) 第二项中的$x_i W^Q.shape:$ (batch_size, h, seq_length, d_z)

$transpose \rightarrow $ (seq_length, batch_size, h, d_z)

$reshape \rightarrow $ (seq_length, batch_size * h, d_z)

之后可以与$A^T$相乘，可以看做是seq_length个并行的(batch_size * h, d_z) matmul (d_a, seq_length)，因为$d_z = d_a$，所以每个并行的运算结果是：(batch_size * h, seq_length), 总的大矩阵的shape: (seq_length, batchsize * h, seq_length).

$reshape \rightarrow $(seq_length, batch_size, h, seq_length)

$transpose \rightarrow$ (batch_size, h, seq_length, seq_length)

与第一项的shape一致，可以相加。

(3)式的推导同理。

下面给出tensor2tensor中对于相对位置编码的代码：https://github.com/tensorflow/tensor2tensor/blob/9e0a894034d8090892c238df1bd9bd3180c2b9a3/tensor2tensor/layers/common_attention.py#L1556-L1587

其中x,对应上面推导中的$x_i * W^Q$, y对应上面推导中的$x_j * W^K$, z对应上面的a。

def _relative_attention_inner(x, y, z, transpose):
  """Relative position-aware dot-product attention inner calculation.
  This batches matrix multiply calculations to avoid unnecessary broadcasting.
  Args:
    x: Tensor with shape [batch_size, heads, length or 1, length or depth].
    y: Tensor with shape [batch_size, heads, length or 1, depth].
    z: Tensor with shape [length or 1, length, depth].
    transpose: Whether to transpose inner matrices of y and z. Should be true if
        last dimension of x is depth, not length.
  Returns:
    A Tensor with shape [batch_size, heads, length, length or depth].
  """
  batch_size = tf.shape(x)[0]
  heads = x.get_shape().as_list()[1]
  length = tf.shape(x)[2]

  # xy_matmul is [batch_size, heads, length or 1, length or depth]
  xy_matmul = tf.matmul(x, y, transpose_b=transpose)
  # x_t is [length or 1, batch_size, heads, length or depth]
  x_t = tf.transpose(x, [2, 0, 1, 3])
  # x_t_r is [length or 1, batch_size * heads, length or depth]
  x_t_r = tf.reshape(x_t, [length, heads * batch_size, -1])
  # x_tz_matmul is [length or 1, batch_size * heads, length or depth]
  x_tz_matmul = tf.matmul(x_t_r, z, transpose_b=transpose)
  # x_tz_matmul_r is [length or 1, batch_size, heads, length or depth]
  x_tz_matmul_r = tf.reshape(x_tz_matmul, [length, batch_size, heads, -1])
  # x_tz_matmul_r_t is [batch_size, heads, length or 1, length or depth]
  x_tz_matmul_r_t = tf.transpose(x_tz_matmul_r, [1, 2, 0, 3])
  return xy_matmul + x_tz_matmul_r_t

结果

使用Attention is All You Need的机器翻译的任务。在training steos每秒去掉7%的条件下，模型的BLEU分数对于English-to-German最高提升了1.3, 对于English-to-French最高提升了0.5.

 [支付宝] 感谢您的捐赠！

But one thing I do: Forgetting what is behind and straining toward what is ahead. ~Bible.Philippians.