CTC (Connectionist Temporal Classification) 算法原理
(原创文章,转载请注明出处哦~)
简单介绍CTC算法
CTC是序列标注问题中的一种损失函数。
传统序列标注算法需要每一时刻输入与输出符号完全对齐。而CTC扩展了标签集合,添加空元素。
在使用扩展标签集合对序列进行标注后,所有可以通过映射函数转换为真实序列的 预测序列,都是正确的预测结果。也就是在无需数据对齐处理,即可得到预测序列。
其目标函数就是 最大化 所有正确的预测序列的概率和。
在查找所有正确预测序列时,采用了前向后向算法。
前向过程计算从1-t时刻,预测出正确的前缀的概率;后向过程计算从t - T时刻,预测出正确的后缀的概率。
那么: 前缀概率 * 后缀概率 / t 时刻预测s的概率 = t 时刻时所有正确的预测序列的概率。
动态规划降低时间复杂度:只有在前一时刻到达预测出某些特定符号,在当前时刻,才可以做出正确预测。
那么,到 t 时刻为止,预测出正确的 标签序列的前缀 的概率 = (到t - 1为止预测正确的所有子序列概率和) * 预测出当前标签的概率。
定义与背景
CTC全称:Connectionist temporal classification, 主要用于处理序列标注问题中的输入与输出标签的对齐问题。
--------------------------------
什么是数据的对齐问题? (参考链接:https://www.cnblogs.com/qcloud1001/p/9041218.html)
传统的语音识别的声学模型训练,对于每一帧的数据,需要知道对应的label才能进行有效的训练,在训练数据之前需要做语音对齐的预处理。
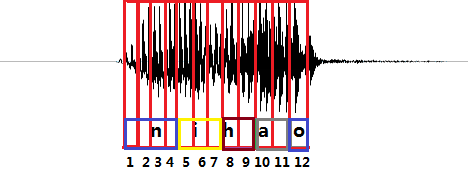
上图是“你好”这句话的声音的波形示意图, 每个红色的框代表一帧数据,传统的方法需要知道每一帧的数据是对应哪个发音音素。比如第1,2,3,4帧对应n的发音,第5,6,7帧对应i的音素,第8,9帧对应h的音素,第10,11帧对应a的音素,第12帧对应o的音素。(这里暂且将每个字母作为一个发音音素)
------------------------------------
传统模型的不足:
1. 训练数据之前需要做语音对齐的预处理,工作比较耗时,并且在缺失对齐标签时,无法做出准确预测;
2. 输出的预测是局部分类,只利用了当前帧的信息,并未利用序列的全局信息(比如相邻两个标签的连续性等,则需要通过其他外加处理。)
------------------------------------------
CTC与传统模型的对比:
1. 与传统的声学模型训练相比,采用CTC作为损失函数的声学模型训练,是一种完全端到端的声学模型训练,不需要预先对数据做对齐,只需要一个输入序列和一个输出序列即可以训练。这样就不需要对数据对齐和一一标注,输入输出之间的alignment不再那么重要。
2. CTC直接输出序列预测的概率,不需要外部的后处理。
--------------------------------------------
CTC的算法原理
<1> 符号定义与目标函数
1. $A$: 序列标注任务中的标签所在字母表集合为 $A$
2. $A'$: 扩展的字母表集合。CTC的softmax 输出层中,比 $A$ 多包含一个标签。我们记为$'blank'$. 即 $A' = A \bigcup \{blank\}$. 那么在输出预测时,前$|A|$个单元输出的是对应字母表$A$中各元素的预测概率,最后一个单元输出的是预测为$'blank'$的概率。
3. $y_k^t$: 网络在 $t$ 时刻输出元素 $k$ 的概率,即在给定长度为 $T$ 的输入序列 $x$ 后,在 $t$ 时刻,预测为 $A'$ 中的元素 $k$ 的概率。
4. $A^{'T}$: 在 $A'$ 集合上的所有长度为 $T$ 的序列集合。
5. 假设在每一个时刻的输出与其他时刻的输出是条件独立的(或者说,条件独立于给定的 $x$ ),那么可以得到在给定输入 $x$ 后,得到 $A^{'T}$ 集合中任何一条路径 $\pi$ 的概率分布: $ \pi \in A^{'T}$ 的分布:
$$p(\pi | x) = \prod_{t = 1} ^ T y_{\pi_t}^t \tag1$$ 。
我们记在$A^{'T}$集合中的序列 $\pi$ 为 $paths$.
6. $l$: 我们记在 $A$ 集合中产生的标签序列为 $l$。
7. 由于在$A^{'T}$ 集合中可能有多条 $paths$,最终所映射的都是同一个序列, 我们需要定义一个多对一的函数,来实现从 $paths$集合到预测序列的映射。$F: A^{'T} \rightarrow A^{\le T}$
其中,我们设定映射后的序列长度不大于映射前的序列长度。
这是要做什么呢?举个例子:
$F(a-ab-) = F(-aa--abb) = aab$
函数映射关系是,将'-'与'-'之间的重复的元素,只保留一个,并且去掉'-'分隔。这样,无论我们的神经网络预测出的序列为‘a-ab-’ 或是 ‘-aa--abb’,它所对应的最终的预测结果都是 'aab',而我们的目标函数也是将 'aab' 与真实标签序列作比较。
这样就不难看出,CTC算法并不要求预测标签与输入的一一对齐关系,而是关注于整个序列的最终预测结果,也就是经过这个函数映射后的结果。
那么我们预测出真实标签序列的概率可以表示为:
$$ p(l|x) = \sum_{\pi \in F^{-1}(l)} p(\pi|x) \tag2$$
即所有的可以映射为真实标签序列的 预测序列的概率和。
<2> blank标签的角色
1. 可以出现重复字符。
设想一下,如果没有'-',对于单词中有重复字符的,比如'apple',其函数映射的结果为'aple',这是不能满足实际情况需要的
2. 如果没有'-',那么神经网络需要一直不停的预测出来一个label,直到下一个不同的label出现。而真实情况中,经常出现一段间隔内(比如语音的停顿处),并没有标签。所以有blank可以满足这样的情况需要。
<3> 前向后向算法的前向过程
由公式(2),我们的目标函数是对所有可以映射为真实标签序列的paths的预测出的概率求和。那么首先,我们要先知道都有哪些paths可以映射为真实标签序列。
对于长度为 $T$ 的输入序列和长度为 $U$ 的标签序列,有2^[(T - U^2 + U(T-3))] * 3^ [(U - 1)(T- U) - 2]种不同路径
有指数级别的路径可能性,不能满足实际需要。为了降低时间复杂度,CTC算法处理时采用了动态规划方法。算法的主要思想是,在筛选可能的paths时,只选取前缀与$l$对应前缀是相同的那些paths. 这样说很难理解,举个例子。
1. 首先,我们构造一个table,希望通过这个table,直观的看出所有可以映射到真实标签序列'apple'的可能路径。
table的横坐标为输入的时间序列,纵坐标为将真实标签序列两两字母以'-'分隔,并且在首尾各加一个'-'。用$U'$标记标签序列经过'-'扩展后的序列。
那么从首'-'或'a'开始,到尾'e'或'-'结束;箭头只能向右,或向下,所有依次经过a, p, p, l, e的那些路径,即为我们要找的,可以映射为真实标签序列的路径。
比如下图1,黑线部分表示的预测的序列为 '- - a p - p l e' (t1时刻预测'-', t2时刻预测为'-', t3时刻预测为'a' ...)。 注意,红色箭头是错误的,因为我们不可能先预测出第3个标签,再预测出第2个标签,标签需要按顺序依次预测出。所以,箭头只能向右或向下!$F( '- - a p - p l e') = 'apple'$
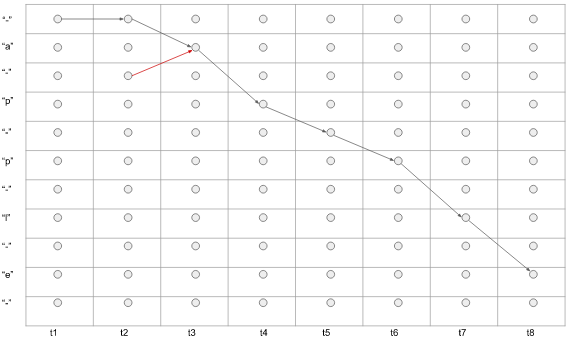
图1.路径举例
那么初始t1时刻,我们只能处于'-'或‘a’的位置,
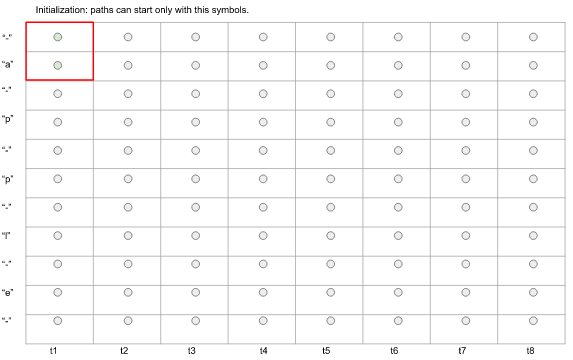
图2. 初始时刻状态
而最终,我们需要依次经过apple所有字母。
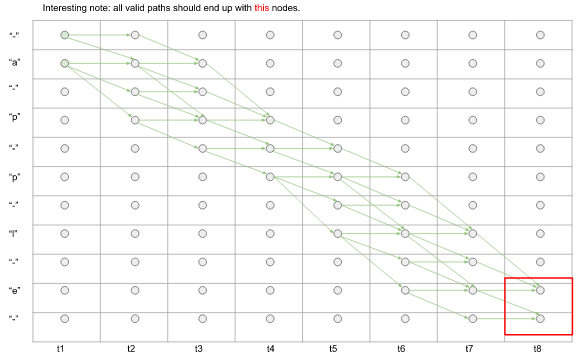
图3.搜索的最终结果状态。
那么,求总路径的问题,也就是找从初始位置,到结束位置的所有的可能路径的问题。
动态规划体现在哪里呢?敲黑板,下面内容是重点~
(1) 对于一条可能路径,其字路径的概率可以表示为,对应时刻神经网络预测标签的概率乘积。比如,如下图所示 $p('- a p - ') = y_-^1 * y_a ^ 2 * y_p^3 * y_-^4$
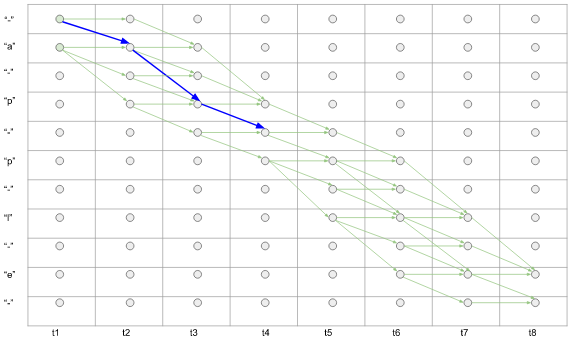
图4. subpath的概率计算
(2) $\alpha_t(s)$: 称为前向变量(forward variable)。表示 前缀末端 在 $t$ 时刻到达序列的第 $s$ 个位置的所有可能子路径的概率和。前缀的意义是,在前$(1-t)$时间内,经过映射后,可以得到真实标签序列的前s / 2个符号。我们把符合这个要求的所有可能路径前缀的概率加和,即为 $\alpha_t(s)$。
那么以此类推,在T时刻,可以到达终止节点'-',或真实标签最后一个符号的,概率和,即为所有可以映射得到真实标签序列的预测序列的概率和,也就是我们需要最大化的目标。
如下图5所示:在 $t3$ 时刻,共有四条路径前缀终止于扩展的标签序列的的第4个节点p.那么$\alpha_3(4) = p('-ap') + p('aap') + p('a-p') + p('app')$ 这四条子路径的前缀经过映射后,都可以得到真实标签序列的前缀:'ap'.
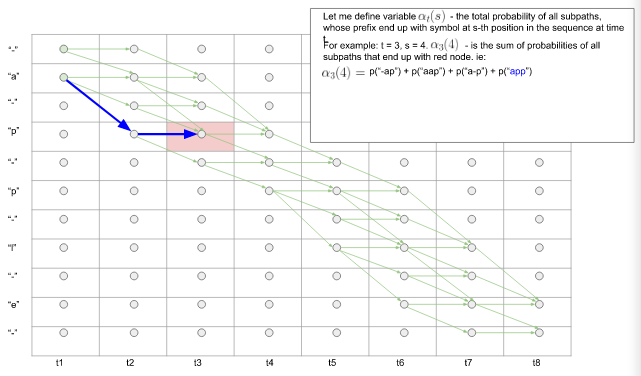
图5.前缀相同的子路径的概率和
(3) 之后,我们需要做的就是,对于每一个cell,都计算其对应的 $\alpha_t(s)$。我们可以递归地进行计算。
即计算可以到达(t, s) 这个cell 的所有子路径概率和 与 在t时刻预测出符号s的概率做乘积,即为在t时刻,到达符号s的所有子路径的概率。
在计算中,有三种情况:
Case1. 第 $s$ 个符号为blank时。
比如 $s = 3, t = 3$,序列的第三个符号为 '-'。见图中红色的cell. $\alpha_3(3)$ 只取决于 $\alpha_2(3)$ (蓝色cell)和 $\alpha_2(2)$ (绿色cell). 那么易得,$\alpha_3(3) = (\alpha_2(3) + \alpha_2(2)) * y_-^3$.
一般的,有$$\alpha_t(s) = (\alpha_{t-1}(s) + \alpha_{t-1}(s-1)) * y_{seq(s)}^t \tag3$$
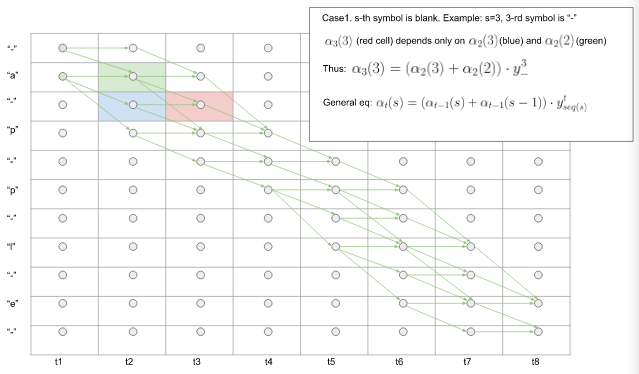
图6. Case1.前向算法中s=‘-’时的$\alpha_s^t$ 计算
Case2. 第s个符号与第(s - 2)个符号相同时,即$seq(s) == seq(s - 2) $。
此时(t,s)cell,只取决于 (t-1, s) (蓝色cell) 和 (t - 1, s - 1)(绿色cell)。一般的:
$$\alpha_t(s) = (\alpha_{t-1}(s) + \alpha_{t-1}(s-1)) * y_{seq(s)}^t \tag4$$
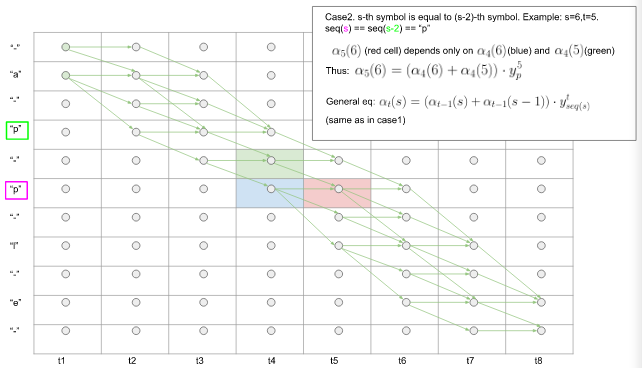
图7. Case2.前向算法中seq(s) == seq(s - 2)时的$\alpha_s^t$ 计算
Case3. 其他情况。有:
$$\alpha_t(s) = (\alpha_{t-1}(s) + \alpha_{t-1}(s-1) + \alpha_{t-1}(s-2) ) * y_{seq(s)}^t \tag5$$
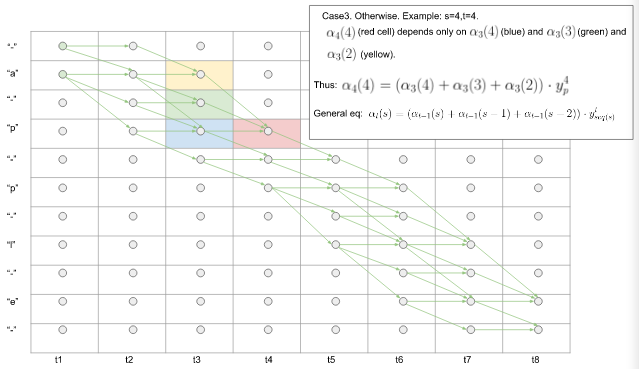
图8. Case3.前向算法中其他情况下 $\alpha_s^t$ 的计算
(4) 通过以上步骤,我们最终可以得到$\alpha_T(U - 1)$ 和 $\alpha_T(U)$。那么预测出真实标签序列的概率为 $$p(l|x) =\alpha_T(U' - 1) + \alpha_T(U') \tag6 $$. 前向过程完成!
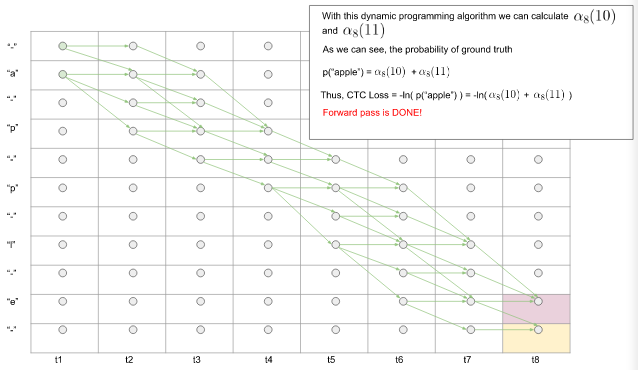
图9. 前向过程完成得到预测出真实序列的概率
<4> 前向后向算法的后向过程
后向算法与前向类似,只是方向不同,后向是找 从序列末端到首端的各个子路径的概率。
定义$\beta_t(s)$为 后缀起始于序列末端, $t$ 时刻到达第 $s$ 个符号的所有可能子路径的概率和。
比如,$t = 6, s = 8, \beta_6(8)$表示所有以下图中红色节点开始的,最终可以到达序列末端的子路径的概率。$\beta_6^(8) = p('lle') + p('l-e') + p('lee') + p('le')$

图10. 反向过程举例
那么,将前向过程中所有箭头反向,使用同样的计算方式,即可计算出反向变量。
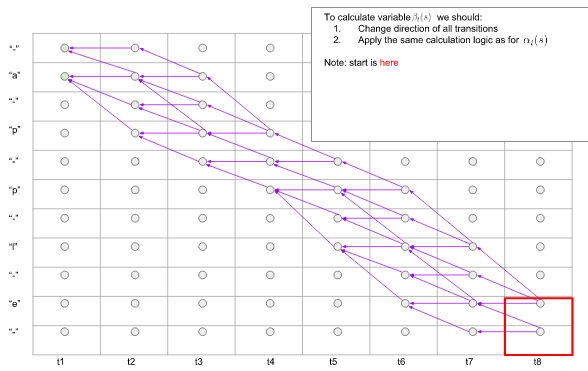
图10. 反向过程
<5> 前向后向算法
<3>部分$\alpha_s(t)$前向变量记录1-t时间内预测出正确前缀的概率(或者可以说,子路径的概率和);<4>部分$\beta_s(t)$后向变量记录t - T时间内预测出正确后缀的概率;
那么
$$\alpha_t(s) * \beta_t(s) / y_t^s\tag7$$
即为 在t时刻,所有正确预测的,并且经过第s符号的,路径的概率和。(除以 y_t^s 因为在 $\alpha$ 和 $\beta$ 中乘了两次)。
举个例子:
$\alpha_{t3}(2) = y_-^{t1} * y_-^{t2} * y_a^{t3} + y_-^{t1} * y_-^{t2} * y_-^{t3}$
$\beta_{t3}(2) = y_a^{t3} * y_p^{t4} * y_-^{t5} * y_p^{t6} * y_l^{t7} * y_e^{t8}$
$\alpha_{t3}(2) * \beta_{t3}(2) = ( y_-^{t1} * y_-^{t2} * y_a^{t3} ) * ( y_a^{t3} * y_p^{t4} * y_-^{t5} * y_p^{t6} * y_l^{t7} * y_e^.{t8}) + (y_-^{t1} * y_-^{t2} * y_-^{t3}) * (y_a^{t3} * y_p^{t4} * y_-^{t5} * y_p^{t6} * y_l^{t7} * y_e^{t8}) = (p('--ap-ple') + p('-aap-ple) + p('aaap-ple')) * y_a^3$
那么 $\alpha_{t3}(2) * \beta_{t3}(2) / y_a^3$ = 在t3时刻,经过符号a的所有正确预测序列的概率和。

图11. 前向后向算法,在t时刻经过第s符号的所有正确预测的路径的概率和
那么将t3时刻,正确预测序列可能会预测出,a, -, p, -,用上面方法,将经过这四个符号的路径概率加和,即可得到在t3时刻,可以做出正确预测的概率。
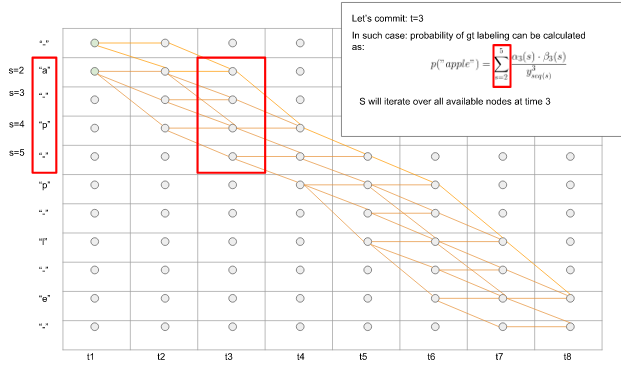
图11. 前向后向算法,在t时刻可以做出正确预测的概率
最后,应用于1 - T的所有时刻,可以得到在任意时刻内预测出正确标签序列的概率。
$$p('apple') = \sum_{s = 1}^{|seq|} \frac{\alpha_s(t) * \beta_s(t)}{y_{seq(s)} ^ t}\tag8$$
<6> 反向传播
我们的目标是最大化$p('apple')$,也就是$ min {-ln(p('apple'))}$,这是我们的目标函数
在反向传播时,我们需要对神经网络的每一个预测输出求偏导。
$$\frac{\partial{(-ln(p('apple')))}}{\partial{y_k^t}} = -\frac{1}{p('apple')} * \frac{\partial{p('apple')}}{\partial{y_k^t}}\tag9$$
我们重点看$$\frac{\partial{p('apple')}}{\partial{y_k^t}} \tag{10}$$的求解。
$p('apple')= \frac{\alpha_{s1}(t) * \beta_{s1}(t)}{y_{s1}^t} + ... + \frac{\alpha_{k}(t) * \beta_{s1}(t)}{y_{k}^t} +... + \frac{\alpha_{sT}(t) * \beta_{sT}(t)}{y_{sT}^t}$
若t时刻过k,则t时刻时不可能经过其他字符的。也就是,在求偏导时,只有红色部分是包含$y_k^t$的,其他项可以看做常数项。
最终,
$$\frac{\partial{p('apple')}}{\partial{y_k^t}} = -\frac{1}{{y_k^t}^2} * \sum_{s:seq(s) = k}\alpha_t(s) * \beta_t(s)\tag{11}$$
举个例子:

这样就完成了!
------------------------------------------
思考:
$\alpha_S(T)$即可可表示所有正确预测序列的概率和,也就是可以表示目标函数,为什么要引入$\beta$呢?
原因:为了反向传播时候求偏导方便呀!否则$\alpha_S(T)$是关于$y_k^t$的一个复杂的函数,很难直接求导的,引入$\beta$后,我们可以关注于t时刻内的偏导计算,会简便许多。
------------------------------------------
<7> 要点总结
1. 动态规划
2. 矩阵 $\alpha$ (前向变量)用于计算loss.
3. 矩阵$\beta$ (后向变量)用来方便计算gradients.
参考链接:
1. Supervised Sequence Labelling with Recurrent Neural Networks:https://www.cs.toronto.edu/~graves/preprint.pdf
2. 语音识别中的CTC算法的基本原理解释:https://www.cnblogs.com/qcloud1001/p/9041218.html
=======================================
 [支付宝]
[支付宝]
您愿意请我吃一根雪糕吗? O(∩_∩)O





