[算法分析与设计] 2. 斐波那契堆及其应用
一个优先队列需要支持的操作有
- insert 插入元素 \(x\)。
- find-min 返回最小的元素。
- delete-min 删除最小的元素。
- decrease-key 将一个元素 \(x\) 减小 \(k\)。\(k \geq 0\)。
常用于实现优先队列的数据结构是堆。
需要注意的是,小根堆需要支持 decrease-key,大根堆需要支持 increase-key。对于一个堆来说两种操作的难度并不一致。以下均考虑小根堆。
还有一个可能支持的操作
- meld 合并两个堆。也叫做 union / merge。
定义 一个堆是一种基于树的数据结构,满足堆性质
- \(A\) 是 \(B\) 的父亲,则 \(A\) 的键值比 \(B\) 的键值小。
一些常见的优先队列实现方法的复杂度表
| 操作 | 链表 | 二叉堆 | 二项堆 | 斐波那契堆† | Brodal queue |
|---|---|---|---|---|---|
| insert | \(O(1)\) | \(O(\log n)\) | \(O(\log n)\) | \(O(1)\) | \(O(1)\) |
| delete-min | \(O(n)\) | \(O(\log n)\) | \(O(\log n)\) | \(O(\log n)\) | \(O(\log n)\) |
| decrease-key | \(O(n)\) | \(O(\log n)\) | \(O(\log n)\) | \(O(1)\) | \(O(1)\) |
| meld | \(O(1)\) | \(O(n)\) | \(O(\log n)\) | \(O(1)\) | \(O(1)\) |
| find-min | \(O(n)\) | \(O(1)\) | \(O(1)\) | \(O(1)\) | \(O(1)\) |
delete 能归约到 decrease-key + delete-min,并且一般不会比这俩优,所以不单独写了。
† 表示均摊复杂度。
我们先不介绍这些堆,先来看我们有了这些黑盒后如何优化一些算法。一般的堆对算法的优化是广为人知的,Brodal queue 的实现又过于复杂并且只是斐波那契堆的复杂度变严格,所以接下来的例子均为斐波那契堆的应用。
一个著名的例子是对 Dijkstra 算法的优化。如果我们用 decrease-key 处理最短路数组的更新,Dijkstra 会进行 \(n\) 次 delete-min,\(n\) 次 insert,\(m\) 次 decrease-key。使用斐波那契堆可以做到 \(O(m + n \log n)\)。
类似地,Prim 算法会进行 \(n\) 次 delete-min,\(n\) 次 insert,\(m\) 次 decrease-key,因此可以做到 \(O(m + n \log n)\)。但和 Dijkstra 不同的是,这不是最优的算法。最小生成树问题弱于排序问题。
优化点在于最小生成树的割性质:对于任意的 \(S \subseteq V\),\(S\) 和 \(V \setminus S\) 之间的边中边权最小的那条一定在任一最小生成树之中。这代表着我们把点集划分为若干个集合,每个集合作为一个新点,跨越两个集合的边连在新点上得到的新图的最小生成树也会在旧图上成立。由此我们可以递归。Borůvka 算法就是这么做的。
我们从一个点开始做 Prim,到堆的大小 \(= k\) 时停止,把涉及到的点与其连出的边合并为一个新点,再在新图中找一个没有被访问过的点继续做 Prim(也需要考虑和新点之间的连边,否则正确性无法保证),这样最后每个新点的度数都 \(\geq k\),因此至多有 \(\frac {2m}k\) 个集合。根据割性质,现在旧图上最小生成树剩下的边可以通过求新图上的最小生成树得到,因此可以递归这个过程。
考虑令 \(k = 2^{\frac {2m}n}\) 则每轮的复杂度 \(O(m + n \log k) = O(m)\),并且
因此第 \(i\) 轮满足 \(\log^{(i)} \frac{2m}{n'} \geq \frac {2m}n\),需要的轮数与 \(\min_i\left\{\log^{(i)} n \leq \frac mn\right\} =: \beta(m, n)\) 同阶,因此总复杂度为 \(O(m \beta(m, n))\)。当 \(m = O(n)\) 时,复杂度也可写为 \(O(m \log^* n)\)。
这个算法仍然不是最优的。
- [Karger, Klein, Tarjan '95] \(O(m)\) 的随机算法。
- [Chazelle '00] \(O(m\alpha(m, n))\) 的确定性算法。
- [Pettie, Ramachandran '02] 证明了的最优算法,但是复杂度确界没有给出,仅知道其在 \(\Omega(m)\) 和 \(O(m \alpha(m, n))\) 中。
- [Dixon, Rauch, Tarjan '92] \(O(m)\) 验证一棵树是否是最小生成树。
接下来我们来介绍二项堆和斐波那契堆。
二项树 \(B_n\) 是递归定义的一种树。\(B_0\) 是一个单点,\(B_n\) 把两棵 \(B_{n-1}\) 的根节点相连,并把其中一棵的根节点认作新的根节点。\(|B_n| = 2^n\)。定义 \(B_n\) 的 \(\mathrm{rank}\) 为 \(n\)。
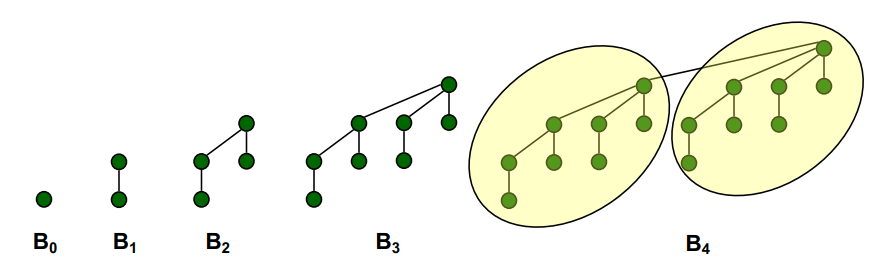
一个二项堆包含若干棵二项树,满足每棵树都满足堆性质,且它们的的 \(\mathrm{rank}\) 互不相同。
由于 \(|B_n| = 2^n\),把二项堆的大小 \(m\) 写成二进制,值为 \(1\) 的那些数位恰好对应一棵二项树。因此二项堆中树的棵数为 \(O(\log m)\)。
meld 如果有两个相同 \(\mathrm{rank}\) 的二项树,那么可以将两者合并,将键值小的作为新的根节点,得到一个 \(\mathrm{rank}+1\) 的仍然满足堆性质的二项树。我们可以将两个堆的大小 \(m_1, m_2\) 写成二进制,列竖式做加法,相同数位的树便也做加法,进位到下一位上。
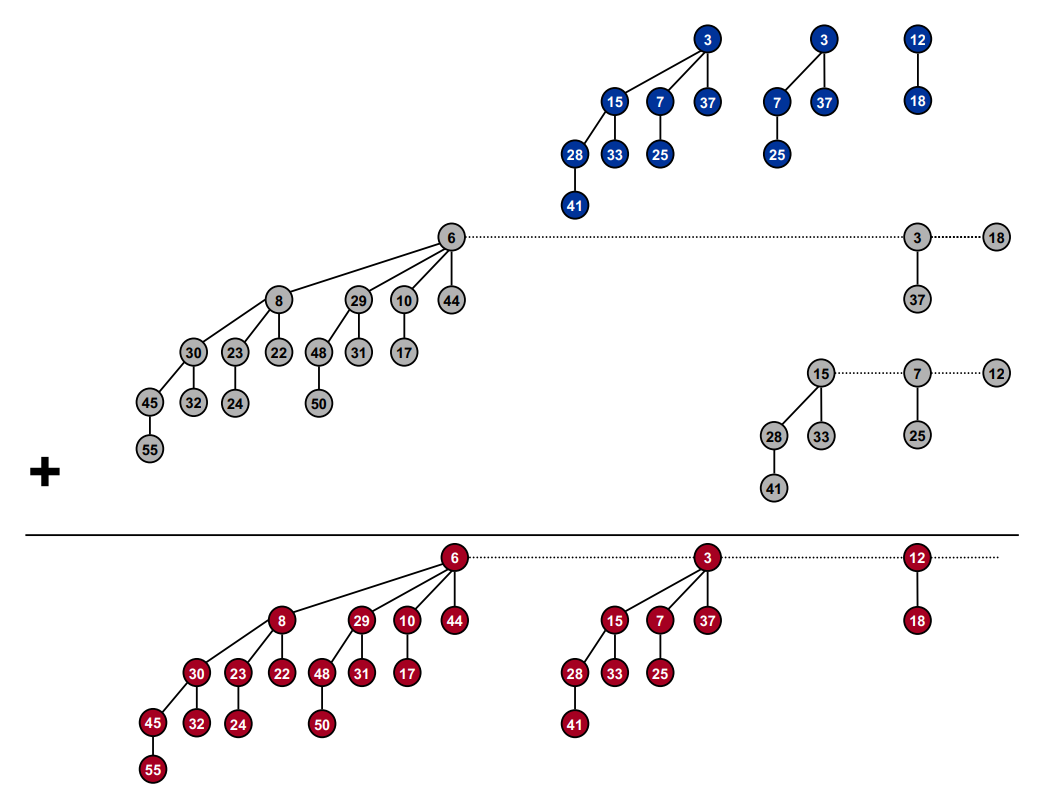
每一次合并的复杂度是 \(O(1)\),因此总复杂度为 \(O(\log m)\)。
insert 将原树和一个仅包含 \(B_0\) 的树做 meld。复杂度为 \(O(\log m)\)。
delete-min 在所有二项树中找到根节点键值最小的,将其所有儿子和剩下的二项树做 meld。复杂度为 \(O(\log m)\)。
find-min 每次 delete-min 的时候维护一下。复杂度为 \(O(1)\)。
decrease-key 向上冒泡。因为树深等于其 \(\mathrm{rank}\),复杂度为 \(O(\log m)\)。
斐波那契堆基于二项堆的思路。它的大致想法是,与其每次都严格维护二项树树形,不如把需要的点直接从树上拆下来,直到 delete-min 的时候再重构,用势能分析得到均摊复杂度。
一个斐波那契堆 \(H\) 仍然包含若干棵树,每一棵树都是删去了一些子树的二项树。那些被删去了儿子的点称为标记点。
定义 \(\mathrm{rank}(x)\) 为 \(x\) 的儿子个数。\(\mathrm{rank}(H) = \max_{x \in H} \mathrm{rank}(x)\)。\(\mathrm{tree}(H)\) 为 \(H\) 拥有的树的棵数,\(\mathrm{marks}(H)\) 为 \(H\) 的标记点的个数。
insert 直接将一个 \(B_0\) 放入 \(H\),\(\mathrm{tree}(H)\) 加一。
delete-min 将其所有儿子放入 \(H\) 中,并将 \(\mathrm{rank}\) 相同的两棵树同二项树一样合并,直到没有 \(\mathrm{rank}\) 相同的两棵树。
decrease-key 如果操作后堆性质仍然满足,不做任何事。否则其键值小于父亲的键值,此时直接将这棵子树从树上拆下来,并将其父亲设为标记点。如果其父亲已经为标记点,则将这个单点也拆下来,删去其标记,并再次考虑它的父亲,循环这个过程直到一个未被标记的点或者根,我们总是不标记根。
这么做的动机是,一棵深的树必须也得是重的。如果删去了太多儿子,可能会导致其结点数很少但是深度很深,从而拖累复杂度。所以我们虽然允许拆子树,但只允许一个结点拆一次,否则这棵子树就要送去重构。在之后的分析中我们会看到满足条件的最小的树的节点个数呈斐波那契数列(直观地,\(|B_n| = |B_{n-1}| + |B_{n-1}| \Rightarrow |B'_n| \geq |B'_{n-1}| + |B'_{n-1\color{red}{-1}}|\)),这也是其名字的由来。
meld 把所有树放到一起就好了。
接下来进行复杂度分析和一些实现细节的描述。
先来考虑形式化上面说的那段话。令 \(F_n\) 表示 \(\mathrm{rank} = n\) 的最小的树的大小,满足性质
- 若 \(y_1, \ldots, y_k\) 是结点 \(x\) 的儿子按照 \(\mathrm{rank}\) 从小到大排序后的序列,则 \(\mathrm{rank}(y_i) \geq \max(0, i - 2)\)。
这条性质是一个序列可以对应斐波那契堆中一棵树在某个时候的形态的充要条件。因为我们总是合并 \(\mathrm{rank}\) 相同的树,当 \(x\) 已有 \(y_1, \ldots, y_{i-1}\) 时,称其为 \(x_i\),合并了 \(y_i\) 则有 \(\mathrm{rank}(y_i) = \mathrm{rank}(x_i) \geq i - 1\),由于 \(y_i\) 至多失去一个孩子,\(\mathrm{rank}(y_i) \geq i - 2\)。而按照这个过程我们也能构建出一棵树与对应的拆子树操作来。
则一个 \(B'_n\) 可以通过某个 \(B'_{n-1}\) 加入第 \(n\) 个儿子得到,即加入某个 \(B'_{n-2}\) 得到,因此有 \(F_n = F_{n-1} + F_{n-2}\),\(F_0 = 1, F_1 = 2\),因此其是斐波那契数列,满足 \(F_n \geq \left(\frac{1 + \sqrt 5}2\right)^n\),故树深总是树重的 \(\log\)。
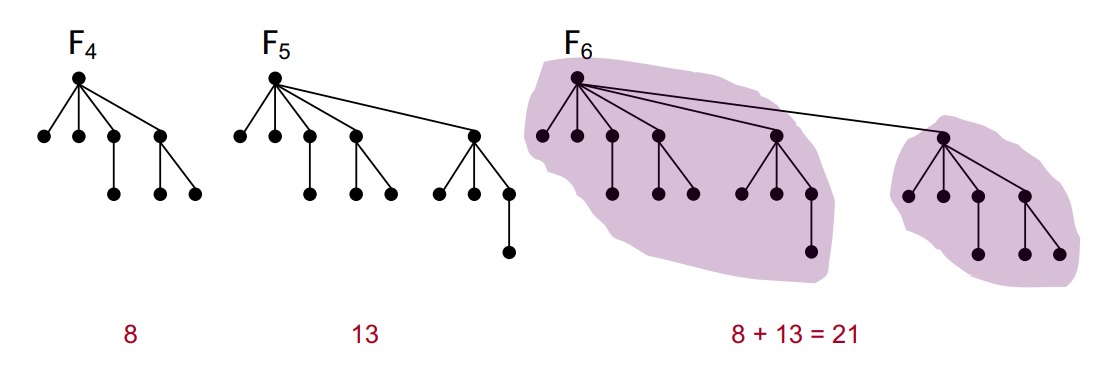
接下来考虑势能函数。有两个操作需要均摊分析,一个是树的个数,一个是标记的个数,前者在 delete-min 中用到,后者在 decrease-key 向上递归时用到。
令 \(\Phi(H) = \mathrm{tree}(H) + 2 \mathrm{marks}(H)\),之所以要加倍数 \(2\) 是因为将标记点拆下来时 \(-\Delta\mathrm{marks}(H) = \Delta\mathrm{tree}(H)\),但我们要统计这部分的实际开销,如果不加倍数则势能不变。因此势能里两者要相差一倍,加给谁都可以,但是既然 \(\mathrm{tree}(H)\) 要承担更多的操作不如让它是一倍的那位。
现在开始考虑每个操作的实际开销与势能变化。
insert 实际开销 \(O(1)\),势能变化 \(+1\),复杂度 \(O(1)\)。
delete-min 实际开销 \(O(\mathrm{rank}(H)) + O(\mathrm{tree}(H))\),势能变化 \(\mathrm{tree}(H') - \mathrm{tree}(H) = O(\mathrm{rank}(H')) - \mathrm{tree}(H)\),均摊复杂度 \(O(\mathrm{rank}(H)) + O(\mathrm{rank}(H')) = O(\log n)\)。
decrease-key 实际开销 \(O(c)\),\(c\) 为涉及的标记点个数,势能变化 \(\leq c + 2(-c + 2) = O(1) - c\),均摊复杂度 \(O(1)\)。需要对儿子维护一个 \(O(1)\) 删除、线性时间遍历的数据结构,一个简单的实现是双向循环链表。
meld 如果使用了双向循环链表那 \(O(1)\) 的合并是简单的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号