关于matlab的PCA入门笔记
版权声明:本文为CSDN博主「生也有涯知也无涯」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_36108664/article/details/104972122
主成分分析法(PCA)
是一种高效处理多维数据的多元统计分析方法,将主成分分析用于多指标(变量)的综合评价较为普遍。
该方法的基本思想是运用较少的变量去解释原始数据中的大部分变异,通过对原始数据相关矩阵内部结构关系的分析和计算,产生一系列互不相关的新变量。根据需要从中选取比原始变量个数少的几个新变量,这些新的变量就是所谓的主成分,它们能够充分解释原始数据的变化。因此,主成分分析法本质上是一种降维方法,也多被用于高维数据的降维处理。
主成分分析的步骤:原始数据(X1,X2,⋯⋯, Xn)标准化,建立变量的相关系数阵,计算特征根和相应的特征向量,确定主成分的个数k(k<n),建立主成分(F1,F2,⋯⋯, Fk)的表达式,建立综合指标F的表达式。
数据
数据的形式一般为多个样本的多个指标,如下是18个输油管段在10个指标上的表现,即一个18*10的矩阵。将其保存到空白txt文件中并保存,作为程序的原始数据。下面的数据来源为论文《基于主成分-聚类分析法的管道风险评价方法》。

数据:
1.5 7.1 280.0 424.0 4.0 430.0 90.0 112.0 459.0 453.0 1.5 7.1 280.0 424.0 4.0 431.0 92.0 112.0 459.0 453.0 1.5 8.7 280.0 424.0 4.0 431.0 92.0 112.0 459.0 453.0 1.5 8.7 280.0 424.0 4.0 431.0 92.0 112.0 459.0 448.0 1.5 8.7 280.0 424.0 4.0 431.0 90.0 112.0 455.0 453.0 2.0 10.3 279.0 425.0 2.0 431.0 90.0 110.0 458.0 449.0 2.0 10.3 277.0 425.0 2.0 431.0 92.0 112.0 458.0 449.0 0.8 10.3 277.0 425.0 2.0 431.0 92.0 112.0 454.0 448.0 2.0 10.3 277.0 425.0 2.0 431.0 92.0 112.0 454.0 448.0 2.0 10.3 277.0 425.0 2.0 431.0 92.0 112.0 458.0 448.0 2.0 10.3 277.0 425.0 2.0 431.0 92.0 377.0 456.0 448.0 2.0 10.3 279.0 425.0 2.0 431.0 92.0 377.0 454.0 449.0 2.0 10.3 279.0 425.0 2.0 431.0 90.0 377.0 456.0 446.0 2.0 10.3 279.0 425.0 2.0 431.0 90.0 112.0 454.0 449.0 2.0 10.3 279.0 425.0 4.0 431.0 92.0 112.0 458.0 449.0 2.0 10.3 279.0 425.0 4.0 430.0 92.0 112.0 458.0 449.0 2.0 10.3 274.0 425.0 4.0 430.0 92.0 112.0 458.0 449.0 1.6 10.3 279.0 424.0 4.0 430.0 92.0 112.0 458.0 449.0
clc,clear
data = load('gd.txt');%将原始数据保存在txt文件中
data=zscore(data); %数据的标准化
r=corrcoef(data); %计算相关系数矩阵r
%下面利用相关系数矩阵进行主成分分析,vec1的第一列为r的第一特征向量,即主成分的系数
[vec1,lamda,rate]=pcacov(r); %lamda为r的特征值,rate为各个主成分的贡献率
f=repmat(sign(sum(vec1)),size(vec1,1),1); %构造与vec1同维数的元素为±1的矩阵
vec2=vec1.*f; %修改特征向量的正负号,使得每个特征向量的分量和为正,即为最终的特征向量
num = max(find(lamda>1)); %num为选取的主成分的个数,这里选取特征值大于1的
df=data*vec2(:,1:num); %计算各个主成分的得分
tf=df*rate(1:num)/100; %计算综合得分
[stf,ind]=sort(tf,'descend'); %把得分按照从高到低的次序排列
stf=stf'; ind=ind'; %stf为得分从高到低排序,ind为对应的样本编号
输出结果分析
代码输出的结果不少,下面按照主成分分析的步骤进行说明。可以结合运行结果来看这部分,表格不少就不贴了。
首先是数据标准化,主成分分析的结果直接受指标量纲的影响。由于各指标的单位可能不一样,因此进行量化评分得到的数据值大小也是不同的。如埋深的单位是米,相应指标在0.8到2.0之间,而人口密度指标的数据值在280左右,这样会导致分析结果的不准确。因此数据的标准化是主成分分析的前提条件,所以实际中可以先把各指标的数据标准化。标准化结果保存在data中。
完成数据的标准化后,对所得结果计算得到标准化数据的相关系数矩阵(相关系数矩阵保存在r中)。相关系数代表了不同指标之间的相关程度,绝对值越大代表相关性越高。相关性较高的变量之间存在信息上的重叠,信息重叠在很大程度上会影响评价结果的客观性,因此相关性矩阵可以证明进行主成分分析的必要性。
由相关系数矩阵可以计算出特征值与特征向量,计算得到与指标数量n相等的n个待选主成分。n个特征值代表了n个主成分对最终评价结果的贡献程度,特征值保存在lamda中,从大到小排列。主成分的特征向量为n*n的矩阵保存在vec1中,表示主成分和相应的原始数据的相关关系,其绝对值越大,则主成分对该指标的代表性越大。为了方便计算,修改特征向量的正负号,使得每个特征向量的分量和为正,即为最终的特征向量,特征向量保存在vec2中,每一列代表一个特征向量,对应一个主成分。
(待选择的)主成分——特征值——贡献率的对应情况见下表。

在主成分的选取上,对应的特征值大小是一个重要衡量因素,普遍的做法是保存特征值要大于1的主成分,舍弃特征值小于1 的主成分,因此最终的主成分个数会小于指标个数n。也可以根据贡献度大小,累计贡献度达到某个程度,不同标准有70%以上,85%以上或其他。这里选取所有特征值大于1的主成分,选取的主成分个数保存在num中,一共有3个。第1主成分对应的就是vec2中的第一列特征向量,以此类推,具体见下表。
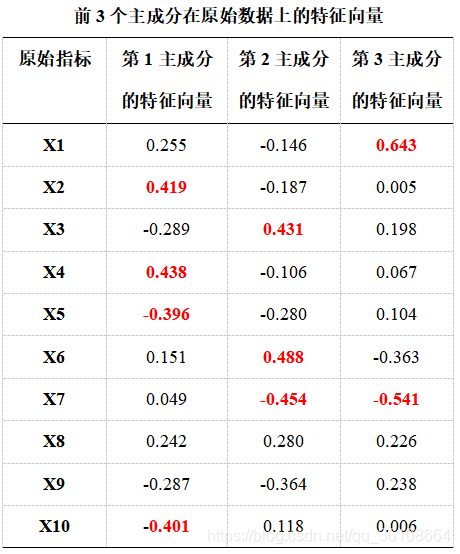
将特征向量作为系数,对应的指标作为自变量,可以得出每一个主成分的计算表达式。将标准化数据Xi代入表达式,就可以得到对应的主成分值。形如
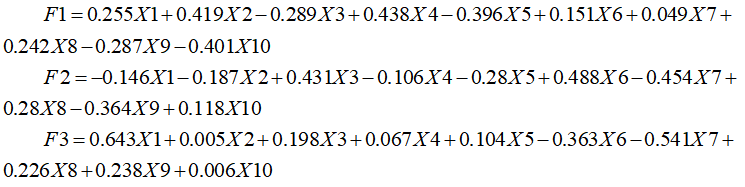
将特征值lamda作为系数,对应的主成分作为自变量,可以确定综合评价值的表达式,F=L1F1+L2F2+……+LkFk,即
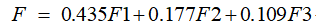
带入之前求得的主成分值,得到每个样本的综合评价值(保存在tf中)。将综合评价值从高到低排序(保存在stf中),并输出对应的样本编号(保存在ind中)。



