【DP】LeetCode 221. 最大正方形
题目链接
思路
分析动态规划题目的时候只需要考虑最后一个阶段，因为所有的阶段转化都是相同的，考虑最后一个阶段容易发现规律
在数组的动态规划问题中，一般 dp[i] 都是表示以 nums 以前 i 个元素组成（即 nums[i - 1]）的状态；dp[i][j] 分别表示以 nums1 前 i 个元素（即 nums1[i - 1]）组成和以 nums2 前 j 个元素（即 nums2[j - 1]）组成的状态，以此类推
字符串也是个数组，是字符数组
表示状态
状态表示就是靠猜，但是会有猜的套路，一般都是通过最终结果和数组数量来猜
因为题目中给出的是矩阵，是二维的数据结构，所以很容易想到使用二维数组 \(dp[i][j]\) 来进行动态规划存储。
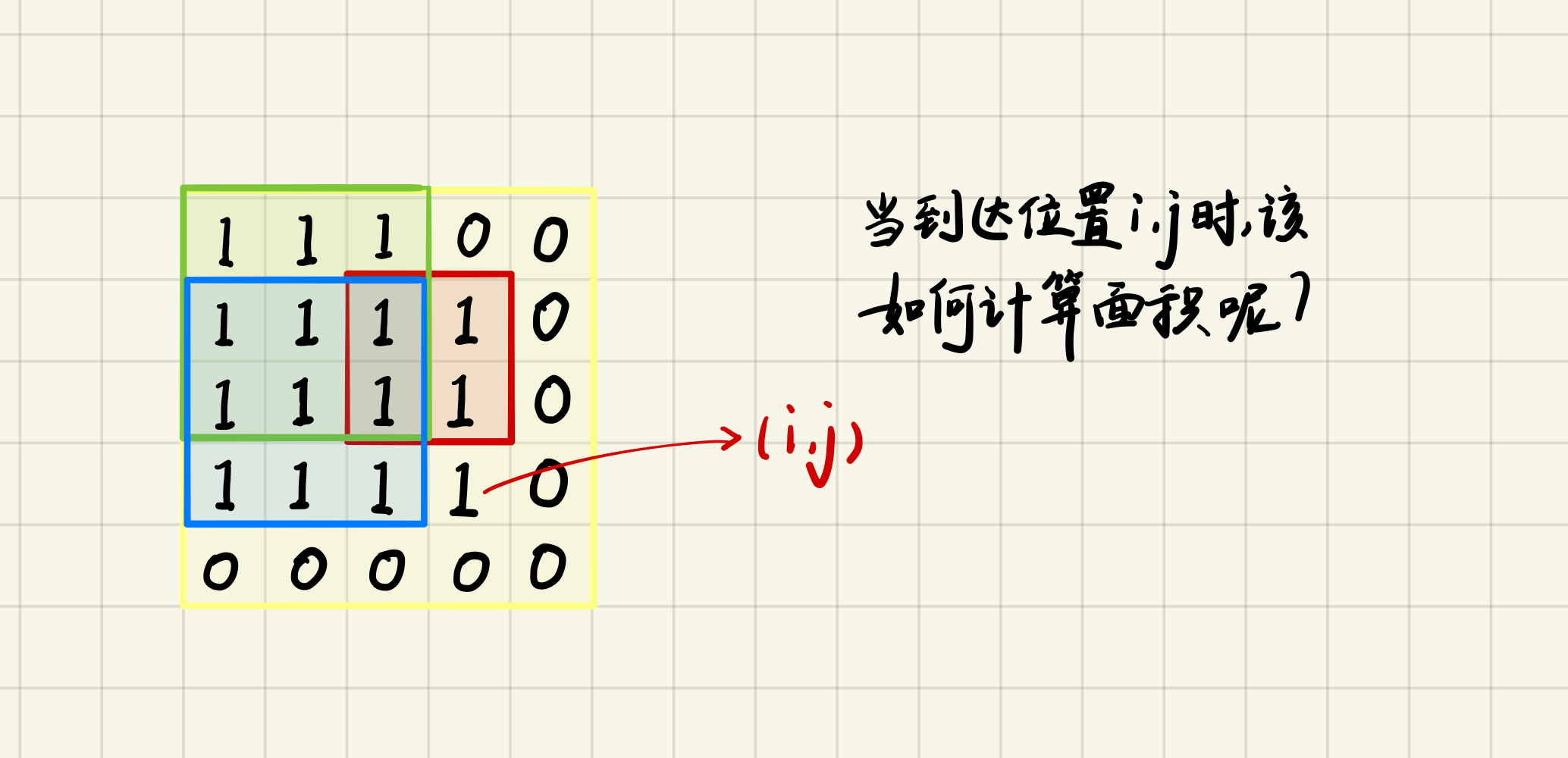
那么具体的含义该怎么定呢？一开始我想表示为以 \((i, j)\) 为右下角的正方形的最大面积，但是发现不好判断 \((i, j)\) 所在正方形内部是否有0，所以这条路是行不通的。
后来想到找的图形是正方形，我们只需要知道正方形的边长就能知道正方形的面积，所以可以把状态定义为以 \((i, j)\) 为右下角的正方形的最大边长。
找状态转移方程
思考的方向是：大问题的最优解怎么由小问题的最优解得到
一开始理解的 \(dp[i][j]\) 是 \(dp[i - 1][j - 1]\) 向右下角进行扩展所得到，但这时候就需要检查 \((i, j)\) 所在前置行单元格和前置列单元格是否有0，不好实现。
这时候思考一下能不能把 \(dp[i][j]\) 和 \(dp[i - 1][j]\) 以及 \(dp[i][j - 1]\) 联系起来，因为 \((i, j)\) 处的正方形边长实际上也是 \((i - 1, j)\) 和 \((i, j - 1)\) 处正方形边长加1。
下图就是一个示例
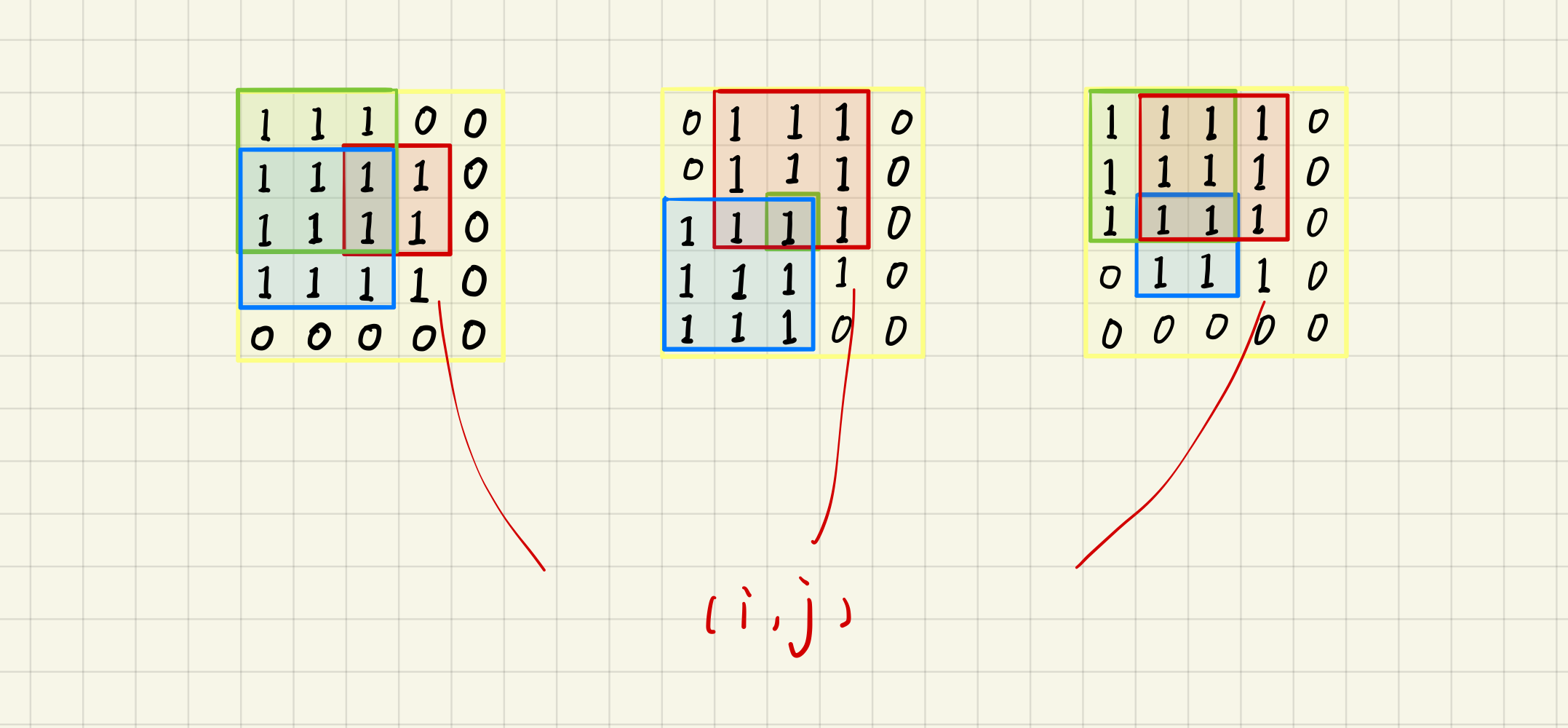
那么我们该如何进行状态转移呢？一开始我想到的是取 \(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]\) 三者最大值再加1，但是万一 \((i, j)\) 的前置行和前置列有0就行不通了，所以我们应该取最小值(这里有一点木桶原理的意思)
就像这幅图一样，如果我们取最大值，会把绿色正方形的第一行也包含进去，但是我们知道绿色正方形旁边是有0的，是行不通的。并且 \((i, j)\) 所在的正方形最多延伸到红色正方形那里，因为红色正方形边长最短。
所以状态转移方程为
但这还不是最终结果，因为 \(dp[i][j]\) 表示的仅仅是以 \((i, j)\) 为右下角的正方形，但最大的正方形可不一定是以 \(dp[m - 1][n - 1]\) 为右下角的正方形，所以我们最后需要取整个 dp 数组的最大值，这样才得到最大边长。
边界处理
对第一行和第一列进行初始化：
代码
dp数组版
class Solution {
public int maximalSquare(char[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
// dp[i][j] 表示以 (i, j) 点为右下角的正方形最大边长
int[][] dp = new int[m][n];
for(int i = 0; i < n; i++){
dp[0][i] = matrix[0][i] - '0';
}
for(int i = 0; i < m; i++){
dp[i][0] = matrix[i][0] - '0';,
}
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
if(matrix[i][j] == '1'){
// 取最小值的原因是防止 (i, j) 所在的行和列中有0
// 如果取最大值,可能小矩阵里没有0,大矩阵里有0,但是依然是按照小矩阵的边长来算
// 类似木桶原理:最大边长取决于边长最短的那个正方形
dp[i][j] = Math.min(
dp[i - 1][j],
Math.min(dp[i][j - 1], dp[i - 1][j - 1])
) + 1;
}
}
}
int result = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
result = Math.max(result, dp[i][j]);
}
}
return result * result;
}
}
