【DP】LeetCode 132. 分割回文串 II

题目链接

132. 分割回文串 II

思路

分析动态规划题目的时候只需要考虑最后一个阶段，因为所有的阶段转化都是相同的，考虑最后一个阶段容易发现规律

在数组的动态规划问题中，一般 dp[i] 都是表示以 nums[i] 为结尾的状态；dp[i][j] 分别表示 以 nums1[i] 和 nums2[j] 为结尾的状态，以此类推

字符串也是个数组，是字符数组

表示状态

状态表示就是靠猜，但是会有猜的套路，一般都是通过最终结果和数组数量来猜

这个题要求的最终结果为最小分割次数，并且只有一个字符串，那么我们可以先尝试定义 $dp[i]$ 表示 $s[0:i]$ 分割成回文子串所需的最小分割次数

找状态转移方程

思考的方向是：大问题的最优解怎么由小问题的最优解得到

即 $dp[i]$ 如何与 $dp[i-1]$、$dp[i-2]$、$dp[i-3]$ 等建立联系

容易想到的一点是：如果 $s[0:i]$ 是个回文串，那么它本身不需要分割，所以 $dp[i]=0$

那如果 $s[0:i]$ 不是个回文串呢？那么我们就尝试分割，枚举分割边界 $j$ 如下图

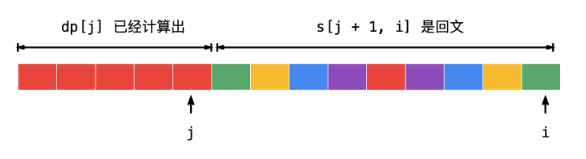
这时候如果到了一个位置，$s[j+1,i]$ 是回文串，那么这时候在 $dp[j]$ 的基础上再 +1 就是 $dp[i]$ 的可能取值

所以状态转移方程为

$$dp[i]=min(dp[i],dp[j+1])$$

边界处理

如果 $s[0:i]$ 是个回文串，那么它本身不需要分割，所以 $dp[i]=0$

我们就令 $dp[i]=i$

判断回文串

这里在判断是否是回文串，即函数 getCheckPalindromeArray 里也使用了动态规划的方法，可以参考这篇文章：【双指针】【DP】LeetCode 5. 最长回文子串

代码

dp数组版

class Solution {
    public int minCut(String s) {
        int n = s.length();
        if(n < 2){
            return 0;
        }
        // dp[i]表示 s[0 : i] 符合要求的最少分割次数
        // dp[i] = min(dp[j] + 1 if s[j + 1: i] 是回文 for j in range(i))
        int[] dp = new int[n + 3];
        // 表示 s[i:j] 是否是回文串
        boolean[][] checkPalindrome = getCheckPalindromeArray(s.toCharArray());

        // 最坏情况下是每个字符单独成串,所以需要每个字符都切割,即需要切 n - 1 下
        for(int i = 0; i < n; i++){
            dp[i] = i;
        }

        // 1 个字符的时候，不用判断，因此 i 从 1 开始
        for(int i = 1; i < n; i++){
            // 如果 s[0 : i] 是回文串,那么就不用切割
            if(checkPalindrome[0][i]){
                dp[i] = 0;
                continue;
            }

            // 如果不是回文串,那么需要判断怎么切割 s[0 : i]
            for(int j = 0; j < i; j++){
                // dp[j], 即 s[0 : j] 的切割次数已经计算好了,现在只需要判断 s[j + 1 : i] 是不是回文串
                // 如果是回文串,那么 dp[i] = min(dp[i], dp[j] + 1)
                if(checkPalindrome[j + 1][i]){
                    dp[i] = Math.min(dp[i], dp[j] + 1);
                }
            }
        }

        return dp[n - 1];
    }

    public boolean[][] getCheckPalindromeArray(char[] s) {
        boolean[][] checkPalindrome = new boolean[s.length][s.length];

        for(int i = 0; i < s.length; i++){
            checkPalindrome[i][i] = true;
        }
        // 枚举每一个子串
        for(int j = 1; j < s.length; j++){
            for(int i = 0; i < j; i++){
                // 如果一个串的左右两个字符相同,且中间的子串是回文串,那么这个串就是回文串
                checkPalindrome[i][j] = (
                        (s[i] == s[j]) && ((j - i <= 2) || checkPalindrome[i + 1][j - 1])
                );
            }
        }

        return checkPalindrome;
    }
}