【DP】LeetCode 97. 交错字符串

题目链接

97. 交错字符串

思路

分析动态规划题目的时候只需要考虑最后一个阶段，因为所有的阶段转化都是相同的，考虑最后一个阶段容易发现规律

在数组的动态规划问题中，一般 dp[i] 都是表示以 nums[i] 为结尾的状态；dp[i][j] 分别表示 以 nums1[i] 和 nums2[j] 为结尾的状态，以此类推

字符串也是个数组，是字符数组

参考类似路径问题，找准状态方程快速求解

表示状态

在遇到两个数组的动态规划问题时，可以通过画矩阵直观进行分析

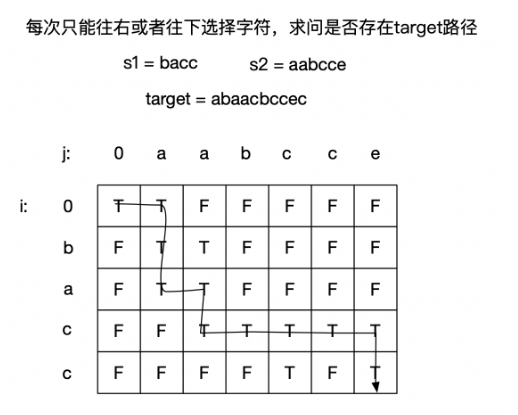
（纠正下：图中 dp[4][3] 位置应该是 T）

我们很容易想到：target 的每个字符都是从 s1（向下）或者 s2（向右）拿到的，所以只要判断是否存在这条 target 路径即可

于是我们可以定义 dp[i][j] 代表 s1 前 i 个字符与 s2 前 j 个字符能否拼接成 s3 前 i + j 个字符

找状态转移方程

根据动态规划问题总结中的描述，状态转移方程应该是个或的形式，即

dp[i][j] = (...) || (...)

按照上面的说法，到达坐标 \((i, j)\) 的走法只能有两种

1. \((i - 1, j)\) 向下走一步，即从 s1 中选择一个字符
2. \((i, j - 1)\) 向右有一步，即从 s2 中选择一个字符

这两种走法只要成立一种就可以，所以上面的伪代码可以变为

dp[i][j] = ((i - 1, j) 向下走一步行得通) || ((i, j - 1) 向右有一步行得通)

而为了保证 \((i - 1, j)\) 向下走一步行得通，我们又需要两个条件

1. 走到\((i - 1, j)\)的路径是通的
2. s1 的这个字符和 s3 的字符相同

所以可以具象为两个条件

(i - 1, j) 向下走一步行得通 = dp[i - 1][j] && c1 == c3

后一个括号同理

(i, j - 1) 向下走一步行得通 = dp[i][j - 1] && c2 == c3

边界处理

很显然，当 s1 和 s2 都是空的时候，答案是 true，即

dp[0][0] = true

当 s1 为空的时候，只需要看 s2 的前多少个字符与 s3 符合，即

for(int i = 1; i <= n1 && s1.charAt(i - 1) == s3.charAt(i - 1); i++){
            dp[i][0] = true;
}

当 s2 为空的时候，只需要看 s1 的前多少个字符与 s3 符合，即

for(int i = 1; i <= n2 && s2.charAt(i - 1) == s3.charAt(i - 1); i++){
            dp[0][i] = true;
}

代码

dp数组版

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        // dp[i][j] 表示 s1 的前 i 个字符和 s2 的前 j 个字符能否组成 s3 的前 i + j 个字符
        int n1 = s1.length();
        int n2 = s2.length();
        if(n1 + n2 != s3.length()){
            return false;
        }
        boolean[][] dp = new boolean[n1 + 1][n2 + 1];

        dp[0][0] = true;
        for(int i = 1; i <= n1 && s1.charAt(i - 1) == s3.charAt(i - 1); i++){
            dp[i][0] = true;
        }
        for(int i = 1; i <= n2 && s2.charAt(i - 1) == s3.charAt(i - 1); i++){
            dp[0][i] = true;
        }
        for(int i = 1; i <= n1; i++){
            for(int j = 1; j <= n2; j++){
                char c1 = s1.charAt(i - 1);
                char c2 = s2.charAt(j - 1);
                char c3 = s3.charAt(i + j - 1);
                dp[i][j] = (dp[i - 1][j] && c1 == c3) || (dp[i][j - 1] && c2 == c3);
            }
        }

        return dp[n1][n2];
    }
}