【DFS】LeetCode 40. 组合总和 II

题目链接

40. 组合总和 II

思路

一道经典的排列组合去重问题，搜索的思路很简单，关键在于如何去重。

借用一下代码随想录的图

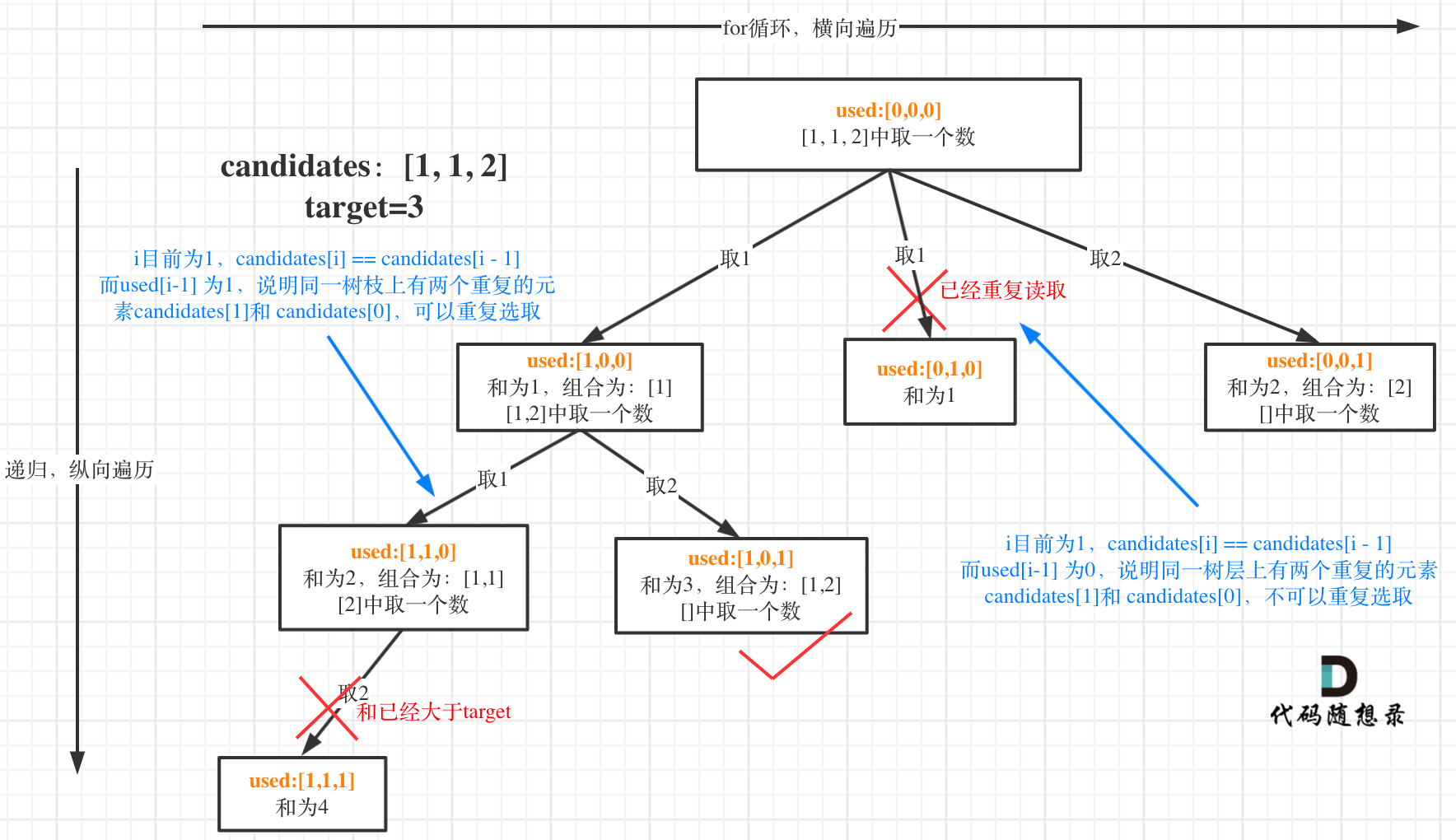
去重的工作实际上就是判断同一层上的相同元素是否已经被用过。即如果 candidates[i] == candidates[i - 1] 并且 used[i - 1] == false 就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过 candidates[i - 1]。

代码

class Solution {
    private List<List<Integer>> result = new ArrayList<>();
    private Deque<Integer> path = new ArrayDeque<>();
    private int sum = 0;
    private boolean[] used;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        used = new boolean[candidates.length];

        dfs(candidates, 0, candidates.length, target);

        return result;
    }

    void dfs(int[] candidates, int index, int len, int target) {
        if(sum > target){
            return;
        }
        if(sum == target){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i = index; i < len; i++){
            if(i > index && candidates[i] == candidates[i - 1] && !used[i - 1]){
                continue;
            }
            path.addLast(candidates[i]);
            sum += candidates[i];
            used[i] = true;
            dfs(candidates, i + 1, len, target);
            used[i] = false;
            sum -= candidates[i];
            path.removeLast();
        }
    }
}

补充

实际上不用 used 数组也是可以的，因为在这个思路里，i > index 的时候，本层首元素已经走完了自己的所有分支，所以后面与本层首元素相等的结点，都可以剪枝去掉。

那么 dfs 函数代码可以变为下面这样。

void dfs(int[] candidates, int index, int len, int target) {
    if(sum > target){
        return;
    }
    if(sum == target){
        result.add(new ArrayList<>(path));
        return;
     }

    for(int i = index; i < len; i++){
        if(i > index && candidates[i] == candidates[i - 1]){
            continue;
        }
        path.addLast(candidates[i]);
        sum += candidates[i];
        dfs(candidates, i + 1, len, target);
        sum -= candidates[i];
        path.removeLast();
    }
}

错误代码

下面这段代码看似与上面相同，实际上犯了过度剪枝的错误，在样例 candidates = [10,1,2,7,6,1,5], target = 8 时，会缺少组合 [2, 6]。因为在错误代码中跳过前面的 1, 1 两个元素后，

index > 0 && candidates[index] == candidates[index - 1] && !used[index - 1]

条件成立，直接 return 不会再对 2 进行搜索。

但是正确代码使用了 for 循环，可以避免这个问题。

    void dfs(int[] candidates, int index, int len, int target) {
        if(sum > target){
            return;
        }
        if(sum == target){
            result.add(new ArrayList<>(path));
            return;
        }
        if(index == len){
            return;
        }

        if(index > 0 && candidates[index] == candidates[index - 1] && !used[index - 1]){
            return;
        }

        sum += candidates[index];
        path.add(candidates[index]);
        used[index] = true;
        dfs(candidates, index + 1, len, target);

        used[index] = false;
        path.pollLast();
        sum -= candidates[index];
        dfs(candidates, index + 1, len, target);
    }