Deep Learning基础--Softmax求导过程
一、softmax函数
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类!
假设我们有一个数组,V,Vi表示V中的第i个元素,那么这个元素的softmax值就是:
$$ S_i = \frac{e^j }{ \sum\nolimits_{j} e^j} \tag{1}$$
更形象的如下图表示:
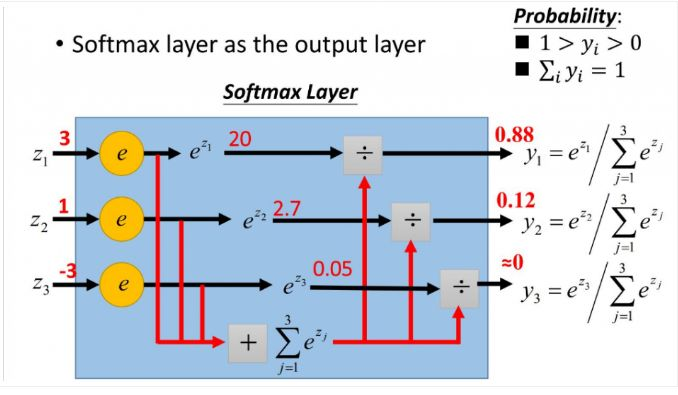
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用,就映射成为(0,1)的值,而这些值的累和为1(满足概率的性质),那么我们就可以将它理解成概率,在最后选取输出结点的时候,我们就可以选取概率最大(也就是值对应最大的)结点,作为我们的预测目标。
二、softmax相关求导
当我们对分类的Loss进行改进的时候,我们要通过梯度下降,每次优化一个step大小的梯度,这个时候我们就要求Loss对每个权重矩阵的偏导,然后应用链式法则。那么这个过程的第一步,就是对softmax求导传回去,不用着急,我后面会举例子非常详细的说明。在这个过程中,你会发现用了softmax函数之后,梯度求导过程非常非常方便。
下面我们举出一个简单例子。
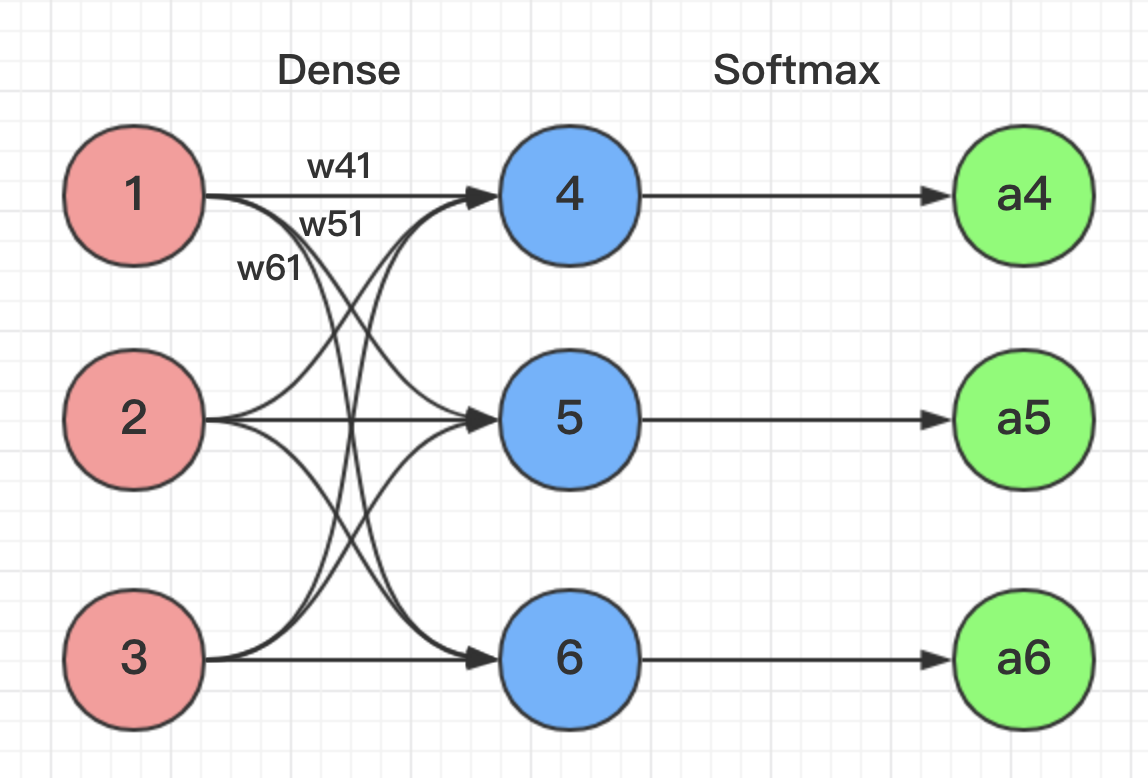
根据图片网络所示,我们能得到下面公式:
z4 = w41*o1+w42*o2+w43*o3
z5 = w51*o1+w52*o2+w53*o3
z6 = w61*o1+w62*o2+w63*o3
z4,z5,z6分别代表结点4,5,6的输出,01,02,03代表是结点1,2,3往后传的输入.
那么我们可以经过softmax函数得到:
$$a_4 = \frac{e^{z_4}}{e^{z_4} + e^{z_5} + e^{z_6}}, a_5 = \frac{e^{z_5}}{e^{z_4} + e^{z_5} + e^{z_6}}, a_6 = \frac{e^{z_6}}{e^{z_4} + e^{z_5} + e^{z_6}} \tag{2}$$
经过上面的形式化后,接下来我们选用交叉熵作为损失函数来推导Softmax的偏导。交叉熵的形式为:
$$ Loss = -\sum_{i} y_i \cdot \ln a_i \tag{3}$$
其中$y$代表我们的真实值,$a$代表我们softmax求出的值。$i$代表的是输出结点的标号。
为了形式化说明,我这里认为训练数据的真实输出为第$j$个为1,其它均为0,那么Loss就变成了$Loss = - y_j \cdot \ln a_j = - \ln a_j$,累和已经去掉,现在我们开始求导数。
参数的形式在该例子中,总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些,那么比如我要求出w41,w42,w43的偏导,就需要将Loss函数求偏导传到结点4,然后再利用链式法则继续求导即可。
举个例子此时求w41的偏导为:
$$
\frac{\partial Loss}{\partial w_{41}} = \frac{\partial Loss}{\partial a_{4}} \cdot \frac{\partial a_4}{\partial z_{4}} \cdot \frac{\partial z_4}{\partial w_{41}}
\\= - \frac{1}{a_4} \cdot \frac{\partial a_4}{\partial z_{4}} \cdot 1 \tag{4}
$$
上式中,只要求出$\frac{\partial a_4}{\partial z_{4}}$就可以完成推导。这里分为两种情况:
1. 当$j=i$时:
$$ \frac{\partial a_j}{\partial z_i} = \frac{\partial}{\partial z_i}(\frac{e^{z_j}}{\sum_k e^{z_k}})
\\=\frac{(e^{z_j})' \cdot \sum_k e^{z_k} - e^{z_j} \cdot e^{z_j}}{(\sum_k e^{z_k})^2}
\\=\frac{e^{z_j}}{\sum_k e^{z_k}} - \frac{e^{z_j}}{\sum_k e^{z_k}} \cdot \frac{e^{z_j}}{\sum_k e^{z_k}}
\\=a_j \cdot (1-a_j)
\tag{5} $$
将(5)式带入(4)中,得到$ \frac{\partial Loss}{\partial w_{j}} = -\frac{1}{a_j} \cdot a_j \cdot (1-a_j) = a_j - 1$。
2. 当$j \neq i$时:
$$ \frac{\partial a_j}{\partial z_i} = \frac{\partial}{\partial z_i}(\frac{e^{z_j}}{\sum_k e^{z_k}})
\\=\frac{0 \cdot \sum_k e^{z_k} - e^{z_j} \cdot e^{z_i}}{(\sum_k e^{z_k})^2}
\\=- \frac{e^{z_j}}{\sum_k e^{z_k}} \cdot \frac{e^{z_i}}{\sum_k e^{z_k}}
\\=-a_j \cdot a_i
\tag{6} $$
将(6)式带入(4)中,得到$ \frac{\partial Loss}{\partial w_{j}} = -\frac{1}{a_j} \cdot -a_j \cdot a_i = a_i$。
OK,到此我们已经完全推导完Softmax部分的反向传播。
参考:
1. https://zhuanlan.zhihu.com/p/25723112
2. https://blog.csdn.net/u014313009/article/details/51045303
