Machine Learning系列--归一化方法总结
一、数据的标准化(normalization)和归一化
数据的标准化(normalization)是将数据按比例缩放,使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理,即将数据统一映射到[0,1]区间上。
目前数据标准化方法有多种,归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法,对系统的评价结果会产生不同的影响,然而不幸的是,在数据标准化方法的选择上,还没有通用的法则可以遵循。
1.1 归一化的目标:统一量纲
归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量。 比如,复数阻抗可以归一化书写:$Z=R+j\omega L=R(1+j\omega L/R)$,复数部分变成了纯数量了,没有量纲。
另外,微波之中也就是电路分析、信号系统、电磁波传输等,有很多运算都可以如此处理,既保证了运算的便捷,又能凸现出物理量的本质含义。
1.2 归一化后有两个好处
1. 提升模型的收敛速度
如下图,$x_1$的取值为0-2000,而$x_2$的取值为1-5,假如只有这两个特征,对其进行优化时,会得到一个窄长的椭圆形,导致在梯度下降时,梯度的方向为垂直等高线的方向而走之字形路线,这样会使迭代很慢,相比之下,右图的迭代就会很快(理解:也就是步长走多走少方向总是对的,不会走偏)。
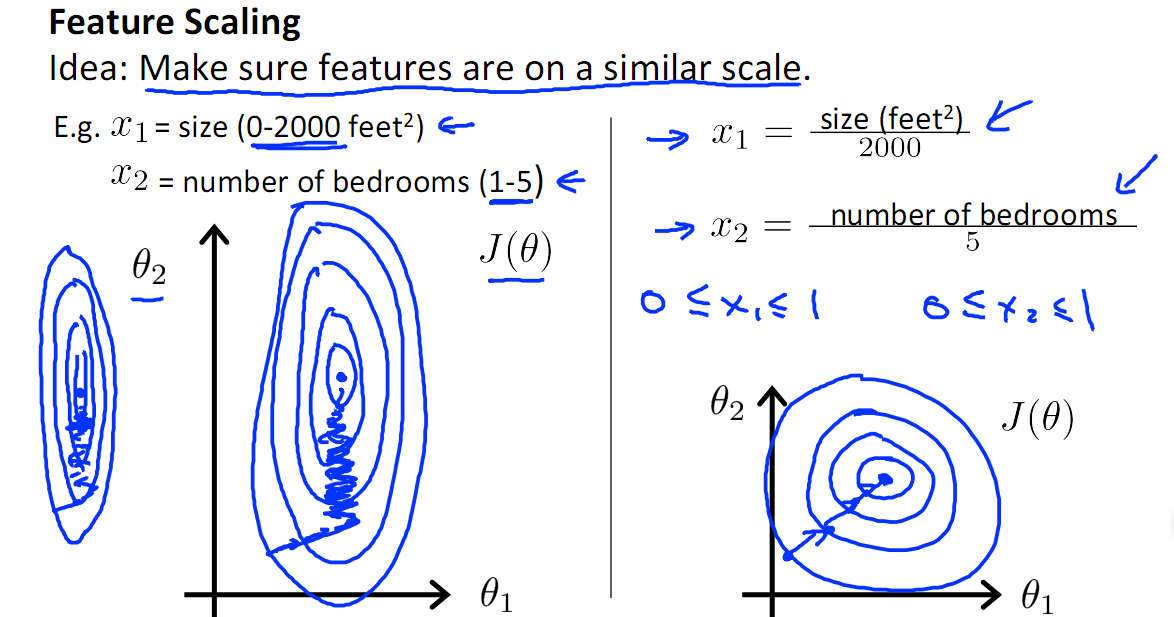
2.提升模型的精度
归一化的另一好处是提高精度,这在涉及到一些距离计算的算法时效果显著,比如算法要计算欧氏距离,上图中$x_2$的取值范围比较小,涉及到距离计算时其对结果的影响远比$x_1$带来的小,所以这就会造成精度的损失。所以归一化很有必要,他可以让各个特征对结果做出的贡献相同。
在多指标评价体系中,由于各评价指标的性质不同,通常具有不同的量纲和数量级。当各指标间的水平相差很大时,如果直接用原始指标值进行分析,就会突出数值较高的指标在综合分析中的作用,相对削弱数值水平较低指标的作用。因此,为了保证结果的可靠性,需要对原始指标数据进行标准化处理。
在数据分析之前,我们通常需要先将数据标准化(normalization),利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题,对不同性质指标直接加总不能正确反映不同作用力的综合结果,须先考虑改变逆指标数据性质,使所有指标对测评方案的作用力同趋化,再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。经过上述标准化处理,原始数据均转换为无量纲化指标测评值,即各指标值都处于同一个数量级别上,可以进行综合测评分析。
从经验上说,归一化是让不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。
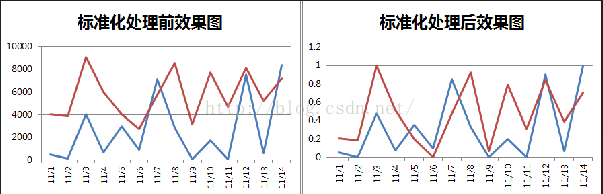
3. 深度学习中数据归一化可以防止模型梯度爆炸。
二、数据需要归一化的机器学习算法
1. 需要归一化的模型:
有些模型在各个维度进行不均匀伸缩后,最优解与原来不等价,例如SVM(距离分界面远的也拉近了,支持向量变多?)。对于这样的模型,除非本来各维数据的分布范围就比较接近,否则必须进行标准化,以免模型参数被分布范围较大或较小的数据dominate。2. 有些模型在各个维度进行不均匀伸缩后,最优解与原来等价,例如logistic regression(因为θ的大小本来就自学习出不同的feature的重要性吧?)。对于这样的模型,是否标准化理论上不会改变最优解。但是,由于实际求解往往使用迭代算法,如果目标函数的形状太“扁”,迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型,最好也进行数据标准化。
2. 不需要归一化的模型:
概率模型不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、rf。而像adaboost、gbdt、xgboost、svm、lr、KNN、KMeans之类的最优化问题就需要归一化。
三、常见的数据归一化方法
3.1 min-max标准化(Min-max normalization)/0-1标准化(0-1 normalization)/线性函数归一化/离差标准化
对原始数据的线性变换,使结果落到[0,1]区间,转换函数如下:
$${x^ * } = \frac{{x - {x_{min}}}}{{{x_{max}} - {x_{min}}}}.$$
其中$x_{max}$为样本数据的最大值,$x_{min}$为样本数据的最小值。
这种方法有一个缺陷就是当有新数据加入时,可能导致$x_{max}$和$x_{min}$的变化,需要重新定义。
3.2 z-score 标准化(zero-mean normalization)
最常见的标准化方法就是Z标准化,也是SPSS中最为常用的标准化方法,spss默认的标准化方法就是z-score标准化。
也叫标准差标准化,这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。
经过处理的数据符合标准正态分布,即均值为0,标准差为1,其转化函数为:
$$ {x^* } = \frac{{x - \mu }}{\sigma }. $$
这两种最常用方法使用场景:
1、在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,第二种方法(Z-score standardization)表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用第一种方法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
原因是使用第一种方法(线性变换后),其协方差产生了倍数值的缩放,因此这种方式无法消除量纲对方差、协方差的影响,对PCA分析影响巨大;同时,由于量纲的存在,使用不同的量纲、距离的计算结果会不同。
而在第二种归一化方式中,新的数据由于对方差进行了归一化,这时候每个维度的量纲其实已经等价了,每个维度都服从均值为0、方差1的正态分布,在计算距离的时候,每个维度都是去量纲化的,避免了不同量纲的选取对距离计算产生的巨大影响。
线性变换后协方差产生倍数值缩放推导如下:
假设数据为2个维度$(X, Y)$,为方便分析,取线性系数$c$,线性变换后的$x'$和$y'$分别为:
$$x' = {c_x} \cdot x.$$
$$y' = {c_y} \cdot y.$$
计算协方差:
$${{\sigma '}_{xy}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{c_x}{x_i} - {c_x}\bar x} \right)} \left( {{c_y}{y_i} - {c_y}\bar y} \right) = {c_x}{c_y}{\sigma _{xy}} \ne {\sigma _{xy}}.$$
可以看到,使用第一种方法(线性变换后),其协方差产生了${c_x}{c_y}$倍的缩放。
3.3 log函数转换
通过以10为底的log函数转换的方法同样可以实现归一下,具体方法如下:
$${x^ * } = \frac{{{{log }_{10}}\left( x \right)}}{{{{log }_{10}}\left( {{x_{max }}} \right)}}.$$
看了下网上很多介绍都是${x^ * } = {log _{10}}\left( x \right)$,其实是有问题的,这个结果并非一定落到[0,1]区间上,应该还要除以${log _{10}}\left( {{x_{max }}} \right)$,$x_{max }$为样本数据最大值,并且所有的数据都要大于等于1。
3.4 atan函数转换
用反正切函数也可以实现数据的归一化:
$$ {x^ * } = \frac{{atan \left( x \right) * 2}}{\pi }. $$
使用这个方法需要注意的是如果想映射的区间为[0,1],则数据都应该大于等于0,小于0的数据将被映射到[-1,0]区间上,而并非所有数据标准化的结果都映射到[0,1]区间上。
3.5 Decimal scaling小数定标标准化
这种方法通过移动数据的小数点位置来进行标准化。小数点移动多少位取决于属性$A$的取值中的最大绝对值。
将属性$A$的原始值$x$使用decimal scaling标准化到$x^ * $的计算方法是:
$$x^ * =\frac{x}{10^j}.$$
其中,$j$是满足条件的最小整数。
例如,假定$A$的值由-986到917,$A$的最大绝对值为986,为使用小数定标标准化,我们用每个值除以1000(即,$j=3$),这样,-986被规范化为-0.986。
注意,标准化会对原始数据做出改变,因此需要保存所使用的标准化方法的参数,以便对后续的数据进行统一的标准化。
3.6 模糊量化模式
$$ {x^ * } = \frac{1}{2} + \frac{1}{2} \cdot sin \left( {\frac{{x - \frac{{{x_{max }} - {x_{min }}}}{2}}}{{{x_{max }} - {x_{min }}}} \cdot \pi } \right). $$
参考博客:
1. 数据标准化/归一化normalization:https://blog.csdn.net/pipisorry/article/details/52247379.
