Deep Learning专栏--强化学习之MDP、Bellman方程(1)
本文主要介绍强化学习的一些基本概念:包括MDP、Bellman方程等, 并且讲述了如何从 MDP 过渡到 Reinforcement Learning。
1. 强化学习基本概念
这里还是放上David Silver的课程的图,可以很清楚的看到整个交互过程。这就是人与环境交互的一种模型化表示,在每个时间点,大脑agent会从可以选择的动作集合A中选择一个动作$a_t$执行。环境则根据agent的动作给agent反馈一个reward $r_t$,同时agent进入一个新的状态。
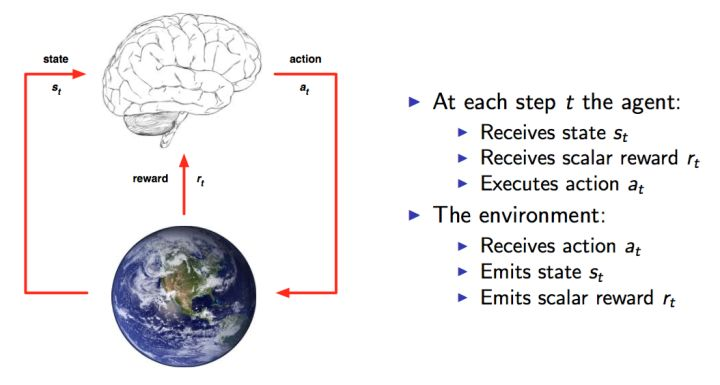
根据上图的流程,任务的目标就出来了,那就是要能获取尽可能多的Reward。Reward越多,就表示执行得越好。每个时间片,agent根据当前的状态来确定下一步的动作。也就是说我们需要一个state找出一个action,使得reward最大,从 state 到 action 的过程就称之为一个策略Policy,一般用$\pi $表示。
强化学习的任务就是找到一个最优的策略Policy从而使Reward最多。
在运行强化学习算法之前,首先需要得到一系列的状态,动作和反馈,这个过程通常是agent随机得到的:
$$ (s_1,a_1,r_1,s_2,a_2,r_2,…s_t,a_t,r_t) $$
这就是一系列的样本Sample。强化学习的算法就是需要根据这些样本来改进Policy,从而使得得到的样本中的Reward更好。
由于这种让Reward越来越好的特性,所以这种算法就叫做强化学习Reinforcement Learning。
2. MDP(Markov Decision Process)
强化学习的问题都可以模型化为MDP(马尔可夫决策过程)的问题,MDP 实际上是对环境的建模;MDP 与常见的 Markov chains 的区别是加入了action 和 rewards 的概念。
因此,一个基本的 MDP 可以用一个五元组$(S,A,P,R, \gamma)$表示,其中:
- $S$是一个有限状态集;
- $A$是一个有限动作集;
- $P$是一个状态转移概率矩阵,$P_a(s, s′)=P(s_{t+1}=s′|s_t=s, a_t=a)$表示在状态$s$下执行动作$a$后转移到状态 $s′$的概率;
- $R$是一个奖励函数,$R_a(s, s′)$ 表示在状态 $s$ 下执行动作 $a$ 后转移到状态 $s′$ 所得到的即时回报(reward);
- $\gamma$是一个折扣因子,一般取值在 [0,1];用来区分当前回报和未来回报的重要性,一般会加在未来的回报前,减小未来回报的权重。
因此,MDP 的核心问题就是找到一个策略 $\pi(s)$ 来决定在状态 $s$ 下选择哪个动作,这种情况下MDP就变成了一个 Markov chain,且此时的目标跟我们前面提到的强化学习的目标是一致的。
3. 回报与价值函数
状态的好坏等价于对未来回报的期望。因此,引入回报(Return) 来表示某个时刻$t$的状态将具备的回报:
$$ G_t = R_{t+1} + \gamma R_{t+2} + … = \sum_{k=0}^\infty\gamma^kR_{t+k+1} $$
上面 $R$ 是 Reward 反馈,$\gamma$ 是 discount factor(折扣因子),跟前面 MDP 中的符号的含义一致。
从上面的式子可以, 除非整个过程结束,否则我们无法获取所有的 reward 来计算出每个状态的 Return,因此,再引入一个概念:价值函数(value function),记为 $V(s)$,通过 $V(s)$ 来表示一个状态未来的潜在价值。从定义上看,value function 就是回报的期望:
$$ V(s) = \mathbb E[G_t|S_t = s] $$
引出价值函数,对于获取最优的策略Policy这个目标,我们就可以通过估计 value function 来间接获得优化的策略。道理很简单,通过价值函数可以知道每一种状态的好坏,这样我们就知道该怎么选择了(如选择动作使得下一状态的潜在价值最大),而这种选择就是我们想要的策略。
我们需要估算 Value Function,只要能够计算出价值函数,那么最优决策也就得到了。因此,问题就变成了如何计算Value Function?
根据前面 $G_t$ 和 $V(s)$ 的定义,有:
$$ \begin{align} V(s) & = \mathbb E[G_t|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma R_{t+2} + \gamma ^2R_{t+3} + …|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma (R_{t+2} + \gamma R_{t+3} + …)|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma G_{t+1}|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma v(S_{t+1})|S_t = s] \end{align} $$
则有:
$$ V(s) = \mathbb E[R_{t+1} + \gamma V(S_{t+1})|S_t = s] $$
上面这个公式就是Bellman方程的基本形态。从公式上看,当前状态的价值和下一步的价值以及当前的反馈Reward有关, 其中透出的含义就是价值函数的计算可以通过迭代的方式来实现。
4. 从 MDP 到 Reinforcement Learning
回到 MDP 问题,如果我们知道了转移概率 $P$ 和奖励函数 $R$,那么便可通过下面的方法求出最优策略 $\pi(s)$, 首先,结合上面提到的价值函数和Bellman方程有:
公式1:
$$ \pi(s):=\arg \max_a\ {\sum_{s’}P_{a}(s,s’)(R_{a}(s,s’)+\gamma V(s’))} $$
公式2:
$$ V(s) := \sum_{s’}P_{\pi(s)}(s,s’)(R_{\pi(s)}(s,s’) + \gamma V(s’)) $$
公式 1 表示在状态 $s$ 下的采取的最优动作,公式 2 表示在状态 $s$ 下的价值,可以看到两者有依存关系;
而在 转移概率 $P$ 和奖励函数 $R$已知的情况下,求解 MDP 问题常见做法有 Value iteration 或 Policy iteration.
4.1 Value iteration
在 Value iteration 中,策略函数 $\pi$ 没有被使用,迭代公式如下:
$$ V_{i+1}(s) := \max_a \sum_{s’} P_a(s,s’)(R_a(s,s’) + \gamma V_i(s’)) $$
下标 $i$ 表示第 $i$ 次迭代,在每轮迭代中需要计算每个状态的价值,并且直到两次迭代结果的差值小于给定的阈值才能认为是收敛。
计算的出收敛的价值函数后,通过公式1就能够得出策略函数 $\pi$ 了,其迭代过程如下图所示:

4.2 Policy iteration
Policy iteration同时更新价值 $V$ 和策略 $\pi$, 且一般可分成两步:
Policy Evaluation,策略评估,就是上面公式2的过程。目的是在策略固定的情况下更新Value Function 直到 value 收敛,从另一个角度来讲就是为了更好地估计基于当前策略的价值
Policy Improvement,策略改进,就是上面公式1的过程。就是根据更新后的 Value Function 来更新每个状态下的策略直到策略稳定
这个方法本质上就是使用当前策略($\pi$)产生新的样本,然后使用新的样本更好的估计策略的价值($V(s)$),然后利用策略的价值更新策略,然后不断反复。理论可以证明最终策略将收敛到最优.
具体的算法流程如下所示:

4.3 区别与局限
问题来了,上面的 Policy Iteration 和 Value Iteration有什么区别, 为什么一个叫policy iteration,一个叫value iteration?
原因其实很好理解,policy iteration 最后收敛的 value $V$ 是当前 policy 下的 value 值(也做对policy进行评估),目的是为了后面的policy improvement得到新的policy;所以是在显式地不停迭代 policy。
而value iteration 最后收敛得到的 value 是当前state状态下的最优的value值。当 value 最后收敛,那么最优的policy也就得到的。虽然这个过程中 policy 在也在隐式地更新,但是一直在显式更新的是 value,所以叫value iteration。
从上面的分析看,value iteration 较 之policy iteration更直接。不过问题也都是一样,都需要知道转移概率 $P$ 和奖励函数 $R$。
但是对于 Reinforcement Learning 这一类问题,转移概率 $P$ 往往是不知道,知道转移概率 $P$ 也就称为获得了模型 Model,这种通过模型来获取最优动作的方法也就称为 Model-based 的方法。但是现实情况下,很多问题是很难得到准确的模型的,因此就有 Model-free 的方法来寻找最优的动作,像 Q-learning,Policy Gradient,Actor Critic这一类方法都是 model-free 的。
前面的方法问题是需要已知转移概率 $P$, 目的是为了遍历当前状态后的所有可能的状态,因此如果采用贪婪的思想,那么就不需要不遍历后面所有的状态,而是直接采取价值最大的状态动作来执行。
Q-learning 实际上就是采用这种思想的,Q-Learning的基本思想是根据 value iteration 得到的,但要明确一点是 value iteration 每次都对所有的Q值更新一遍,也就是所有的状态和动作。但事实上在实际情况下我们没办法遍历所有的状态,还有所有的动作,因此,我们只能得到有限的系列样本。具体的算法流程会再下一篇文章具体介绍。
综上,本文主要介绍了强化学习的任务和一些概念,以及从 MDP 如何过渡到 Reinforcement,在后续的文章中会介绍value-based的Q-learning 和DQN方法,Policy gradient 类方法以及结合两者的 Actor Critic 及DDPG方法。
参考资料:
2. DQN 从入门到放弃4 动态规划与Q-Learning
