什么是梯度下降法与delta法则？

梯度下降法就是沿梯度下降的方向求解函数（误差）极小值。delta法则是使用梯度下降法来找到最佳权向量。拿数字识别这个案例为例，训练模型的过程通常是这样的。输入为1万张图片，也就是1万个样本，我们定义为D，是训练样例集合，输出为相对应的1万个数字。这就是1万个目标输出(Target），每一个目标输出我们定义为：td ，是训练样例d的目标输出。我们的模型训练的目的是想找出，此人工神经网络模型的参数，比如权向量w等。要注意，目标输出td是已知的（非变量，比如5这张图，目标输出就是5这个数字），样本也是已知的。参数是未知的。还有什么是未知的?这就需要从训练的过程入手了。训练过程，通常开始时，所有的权向量w都从一个很小的值开始，比如零，这时有一个实际输出（od是对训练样例d的实际输出）。目标输出和实际输出的差距叫做误差。因为一共有1万个样本，为了消除正负误差相抵，所以我们定义所有目标输出和实际输出的误差平方和的一半为E。（因为平方的求导会出现2，所以这就是取一半的原因，这样2×(1/2)会使系数消失。）

 

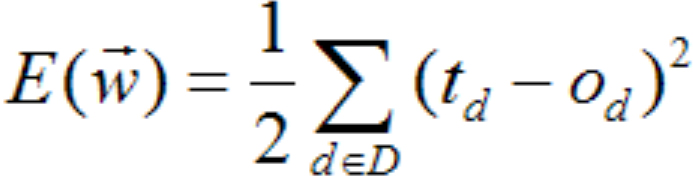
拿我们这章第一个例子，单个神经元的房子预测神经网络模型为例，不难理解：Od=x0*w0+x1*w1+…xn*wn+b，结合前面的分析可知，x0，x1，。。。。。xn都是一个个的样本值， 是已知的。td也是已知的。这样看E是w0,w1,....wn和b的函数。我们的目标就是找到一组权向量（w0,w1,....wn和b）能使E最小化。拿wi来说，我们可以画一条函数曲线：。。。。。。。。。。。。。。。。。。。

更多内容请见原文，文章转载自原文：https://blog.csdn.net/qq_44639795/article/details/100599848