点是否在面内算法(Point-In-Polygon Algorithm)

本文源自：http://alienryderflex.com/polygon/

© 1998,2006,2007 Darel Rex Finley.  This complete article, unmodified, may be freely distributed for educational purposes.

Visit the new page which adds spline curves to this technique!  Also visit the shortest-path-through-polygon page!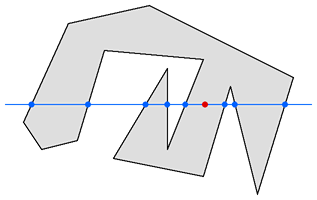


Figure 1

Figure 1 demonstrates a typical case of a severely concave polygon with 14 sides.  The red dot is a point which needs to be tested, to determine if it lies inside the polygon.

The solution is to compare each side of the polygon to the Y (vertical) coordinate of the test point, and compile a list of nodes, where each node is a point where one side crosses the Y threshold of the test point. In this example, eight sides of the polygon cross the Y threshold, while the other six sides do not.  Then, if there are an odd number of nodes on each side of the test point, then it is inside the polygon; if there are an even number of nodes on each side of the test point, then it is outside the polygon.  In our example, there are five nodes to the left of the test point, and three nodes to the right.  Since five and three are odd numbers, our test point is inside the polygon.

(Note:  This algorithm does not care whether the polygon is traced in clockwise or counterclockwise fashion.)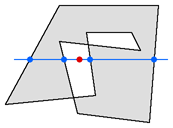


Figure 2

Figure 2 shows what happens if the polygon crosses itself.  In this example, a ten-sided polygon has lines which cross each other.  The effect is much like “exclusive or,” or XOR as it is known to assembly-language programmers.  The portions of the polygon which overlap cancel each other out.  So, the test point is outside the polygon, as indicated by the even number of nodes (two and two) on either side of it.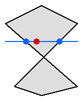


Figure 3

In Figure 3, the six-sided polygon does not overlap itself, but it does have lines that cross.  This is not a problem; the algorithm still works fine.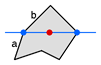


Figure 4

Figure 4 demonstrates the problem that results when a vertex of the polygon falls directly on the Y threshold.  Since sides a and b both touch the threshold, should they both generate a node?  No, because then there would be two nodes on each side of the test point and so the test would say it was outside of the polygon, when it clearly is not!

The solution to this situation is simple.  Points which are exactly on the Y threshold must be considered to belong to one side of the threshold.  Let’s say we arbitrarily decide that points on the Y threshold will belong to the “above” side of the threshold.  Then, side a generates a node, since it has one endpoint below the threshold and its other endpoint on-or-above the threshold.  Side bdoes not generate a node, because both of its endpoints are on-or-above the threshold, so it is not considered to be a threshold-crossing side.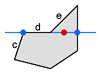


Figure 5

Figure 5 shows the case of a polygon in which one of its sides lies entirely on the threshold.  Simply follow the rule as described concerning Figure 4.  Side c generates a node, because it has one endpoint below the threshold, and its other endpoint on-or-above the threshold.  Side d does not generate a node, because it has both endpoints on-or-above the threshold.  And side e also does not generate a node, because it has both endpoints on-or-above the threshold.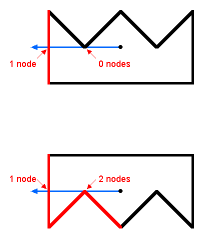


Figure 6

Figure 6 illustrates a special case brought to my attention by John David Munch of Cal Poly.  One interior angle of the polygon just touches the Y-threshold of the test point.  This is OK.  In the upper picture, only one side (hilited in red) generates a node to the left of the test point, and in the bottom example, three sides do.  Either way, the number is odd, and the test point will be deemed inside the polygon.


Polygon Edge

If the test point is on the border of the polygon, this algorithm will deliver unpredictable results; i.e. the result may be “inside” or “outside” depending on arbitrary factors such as how the polygon is oriented with respect to the coordinate system.  (That is not generally a problem, since the edge of the polygon is infinitely thin anyway, and points that fall right on the edge can go either way without hurting the look of the polygon.)


C Code Sample

//  Globals which should be set before calling this function:
//
//  int    polySides  =  how many corners the polygon has
//  float  polyX[]    =  horizontal coordinates of corners
//  float  polyY[]    =  vertical coordinates of corners
//  float  x, y       =  point to be tested
//
//  (Globals are used in this example for purposes of speed.  Change as
//  desired.)
//
//  The function will return YES if the point x,y is inside the polygon, or
//  NO if it is not.  If the point is exactly on the edge of the polygon,
//  then the function may return YES or NO.
//
//  Note that division by zero is avoided because the division is protected
//  by the "if" clause which surrounds it.

bool pointInPolygon() {

  int      i, j=polySides-1 ;
  boolean  oddNodes=NO      ;

  for (i=0; i<polySides; i++) {
    if (polyY[i]<y && polyY[j]>=y
    ||  polyY[j]<y && polyY[i]>=y) {
      if (polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])<x) {
        oddNodes=!oddNodes; }}
    j=i; }

  return oddNodes; }

Here’s an efficiency improvement provided by Nathan Mercer.  The blue code eliminates calculations on sides that are entirely to the right of the test point.  Though this might be occasionally slower for some polygons, it is probably faster for most.

//  Globals which should be set before calling this function:
//
//  int    polySides  =  how many corners the polygon has
//  float  polyX[]    =  horizontal coordinates of corners
//  float  polyY[]    =  vertical coordinates of corners
//  float  x, y       =  point to be tested
//
//  (Globals are used in this example for purposes of speed.  Change as
//  desired.)
//
//  The function will return YES if the point x,y is inside the polygon, or
//  NO if it is not.  If the point is exactly on the edge of the polygon,
//  then the function may return YES or NO.
//
//  Note that division by zero is avoided because the division is protected
//  by the "if" clause which surrounds it.

bool pointInPolygon() {

  int      i, j=polySides-1 ;
  boolean  oddNodes=NO      ;

  for (i=0; i<polySides; i++) {
    if ((polyY[i]< y && polyY[j]>=y
    ||   polyY[j]< y && polyY[i]>=y)
    &&  (polyX[i]<=x || polyX[j]<=x)) {
      if (polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])<x) {
        oddNodes=!oddNodes; }}
    j=i; }

  return oddNodes; }

Here’s another efficiency improvement provided by Lascha Lagidse.  The inner “if” statement is eliminated and replaced with an exclusive-OR operation.

//  Globals which should be set before calling this function:
//
//  int    polySides  =  how many corners the polygon has
//  float  polyX[]    =  horizontal coordinates of corners
//  float  polyY[]    =  vertical coordinates of corners
//  float  x, y       =  point to be tested
//
//  (Globals are used in this example for purposes of speed.  Change as
//  desired.)
//
//  The function will return YES if the point x,y is inside the polygon, or
//  NO if it is not.  If the point is exactly on the edge of the polygon,
//  then the function may return YES or NO.
//
//  Note that division by zero is avoided because the division is protected
//  by the "if" clause which surrounds it.

bool pointInPolygon() {

  int      i, j=polySides-1 ;
  boolean  oddNodes=NO      ;

  for (i=0; i<polySides; i++) {
    if ((polyY[i]< y && polyY[j]>=y
    ||   polyY[j]< y && polyY[i]>=y)
    &&  (polyX[i]<=x || polyX[j]<=x)) {
      oddNodes^=(polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])<x); }
    j=i; }

  return oddNodes; }

Integer Issue

What if you’re trying to make a polygon like the blue one below (Figure 7), but it comes out all horizontal and vertical lines, like the red one?  That indicates that you have defined some of your variables as integers instead of floating-point.  Check your code carefully to ensure that your test point and all the corners of your polygon are defined as, and passed as, floating-point numbers.

   Figure 7