C-means

 

 

 

二 算法

2.1. 模糊集^[1]

定义：在论域X上的模糊集合是X到[0,1]的一个映射，称作隶属函数，记作：

 

对于称为x对于的隶属度，隶属度越接近于1，表示x属于的程度越高，越接近于0表示x属于的程度越低。用取值于区间[0,1]的隶属函数表征x 属于的程度高低。由于许多事物受多种因素影响，所以无法给出绝对地肯定或否定的评价，这就需要用一个模糊集合来表示。

       例如：如何定义年轻人含义，提出符合“年轻人”这一概念的最合适的年龄区间。

我们假设27岁的隶属度为0.85，那就是27岁的人和年轻人有0.85的相似程度，0.15的不相似程度，且这里的0.85是权重而不是概率。

隶属函数经常是初步粗略设定,然后再通过学习和训练逐步修改和完善，可以使用模糊统计法，x对的隶属频率：

 

是元素x属于的次数，n是试验总次数。

 

 

 

2.2. k-means算法^[2]

原理：将样本分为k个类，使得每个样本到所属类的中心的距离最小且每个样本只属于一个类。

模型：给定n个样本集合，每个样本都是一个特征向量。将n个样本分到k个不同的类中，使得k个类是对集合X的一个划分。一个划分C是一个多对一的函数，可以用函数，即k-means聚类模型是一个从样本到类的函数。

决策：可以给定一个大概的集合X的划分，通过损失函数最小化来改善得到最优的划分。

 

 

 

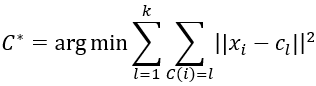
其中表示属于类的，表示类的中心。

算法：损失函数中存在两个变量，的具体数据不确定，以及类中心无法确定。所以首先选择k个类的中心，得到一个聚类的结果，然后把每个类的样本均值作为类的新的中心，进行迭代使得划分最后收敛，得出结果。该算法复杂度为O(mnk)，其中m是样本维度，n为样本个数，k为类的数量。

 

 

 

2.3. Fuzzy C-means算法

原理：将样本分为c个类，使得每个样本到所属类的中心的距离乘以相应的隶属度最小且每个样本只属于一个类。

模型：在k-means聚类算法的基础上把多对一的函数改成了所有样本对各个类的隶属度矩阵U，即将模糊集和k-means算法结合起来，使得损失的函数变为隶属矩阵和类的中心。

决策：可以给定一个大概的集合X的划分，通过损失函数最小化来改善得到最优的划分。

 

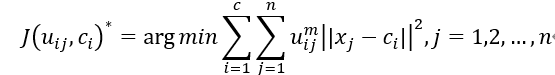
注：具体的算法见2.4. 推导过程。

 

2.4. Fuzzy C-means推导过程

  

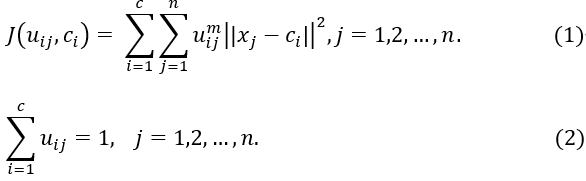
其中(1)表示损失函数，(2)表示限制条件；m是模糊因子影响聚类性能，范围，通常取m=2；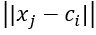

表示在类上的程度，即第j组数据在第i类上的隶属度。

得到隶属度矩阵：

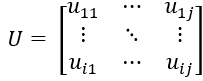
对于上述模型我们可以采用拉格朗日乘数法引入新的变量去除限制条件,得：

 

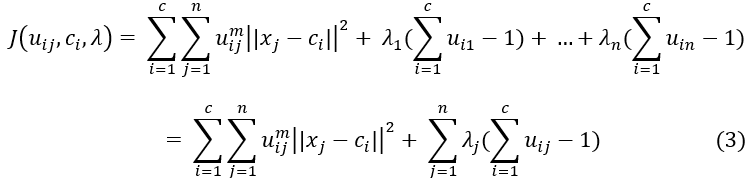
其中λ为拉格朗日乘子。为了使其收敛即求解，我们需要得到式子(3)的最小值，求偏导。

 

 

 

 

图1

 

 

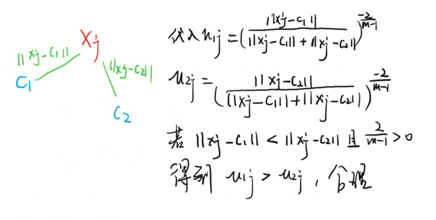
图2

小结：

算法步骤

1. 确定分类数c，以及迭代的次数。

2. 随机(根据经验)确定隶属矩阵。

3. 根据隶属度矩阵U用式子(7)计算类的中心c。

4. 再用类的中心c通过式子(6)计算更新隶属度矩阵U。

5. 重复过程3,4，直到损失函数收敛得到最优结果。

 

 

 

 

 

 

 代码

clear clc;
close all; 

color = [0 0 1;
0 1 0;
1 0.5 0;
0 1 1;
1 0 1;
0.5 0 0.5;] ; % 自定义颜色

data = rand(100,2);  %随机产生100个2维样本
cluster_n = 4;   %分类数
[center,U,fcn_J] = fcm1(data,cluster_n);
figure;
subplot(1,2,1),plot(data(:,1), data(:,2),'o');
title('分类结果');
hold on;
maxU = max(U);

for i = 1:size(center,1)
index = find(U(i,:) == maxU); 
line(data(index,1),data(index,2),'color',color(i,:)); % 将相同类的点连起来
end

plot(center(:,1),center(:,2),'*','color','r');  % 标记出类的中心
legend('样本点','c1','c2','c3','c4','中心点','Location','Best');  % 手动改变
subplot(1,2,2), plot(fcn_J);
title('损失函数J');
hold off;


function [center, U, fcn_J] = fcm1(data, cluster_n, options)

if nargin ~= 2 && nargin ~= 3   % 判断函数输入变量
    error('输入变量的数量不对');
end

default_options = [2; 200; 1e-5; 1];% 设定默认值
% 分别是平滑因子，迭代次数，收敛标准，是否显示迭代过程(0为否，1为是)

if nargin == 2     % 使用默认值
    options = default_options;
else
    if length(options) < 4   % options中变量输入正确
        tmp = default_options;
        tmp(1:length(options)) = options;
        options = tmp;
    end
    % 将options中为nan的变量用默认值替代
    nan_index = find(isnan(options)==1);
    options(nan_index) = default_options(nan_index);
    if options(1) <= 1 % 判断分类数是否大于等于1
        error('分类数需要大于等于1！');
    end
end

data_n = size(data, 1);     % 样本数量
data_d = size(data, 2);     % 样本维度

expo = options(1);            % 平滑因子
max_iter = options(2);        % 最大迭代次数
min_criteria = options(3);   % 收敛标准
display = options(4);        % 是否显示迭代过程

fcn_J = zeros(max_iter, 1);            % 初始化损失函数

% 随机初始化隶属度矩阵U
U = rand(cluster_n, data_n);
col_sum = sum(U);
U = U./col_sum(ones(cluster_n, 1), :);     %限制条件(2)

%迭代
for i = 1:max_iter
    mf = U.^expo;           % 平滑处理m，隶属度矩阵中每个数据乘以次方
    center = mf*data./(sum(mf,2)*ones(1,size(data,2)));   % 更新新的中心,式子(7)
    % 其中data = [x1';x2';...;xj']
    % sum(mf,2)表示按照行相加，得到[sum_mf1;sum_mf2;...;sum_mfi]
    % sum(mf,2)*ones(1,size(data,2),即为i*1与1*i矩阵相乘得到i*i

    dist = distfcm1(center, data);       % 计算欧式距离
    % dist = [||c1-x1||,...,||c1-xj||;...;||ci-x1||,...,||ci-xj||]
    fcn_J(i) = sum(sum((dist.^2).*mf));  % 计算损失函数J
    % 两个sum第一个是先加i，得到[sum1,sum2,...,sumj]
    % 第二个sum再把j加起来

    % 更新新的隶属度矩阵，式子(6)
    tmp = dist.^(-2/(expo-1));     % ||ci-xj||^(-2/(m-1))
    U = tmp./(ones(cluster_n, 1)*sum(tmp)); % 根据式子(6),进行更新
    
    if display 
        fprintf('迭代次数 = %d, 损失函数 = %f\n', i, fcn_J(i));
    end
    
    % 判断是否收敛
    if i > 1
        if abs(fcn_J(i) - fcn_J(i-1)) < min_criteria
            break; 
        end
    end
end

fcn_J(i+1:max_iter) = []; % 将未迭代的矩阵空间变为空
end


function out = distfcm1(center, data)%计算欧式距离
out = zeros(size(center, 1), size(data, 1));
for k = 1:size(center, 1)
    out(k, :) = sqrt(sum(((data-ones(size(data, 1), 1)*center(k, :)).^2), 2)); 
    %分别计算所有点到第k类的距离
end
end

代码2

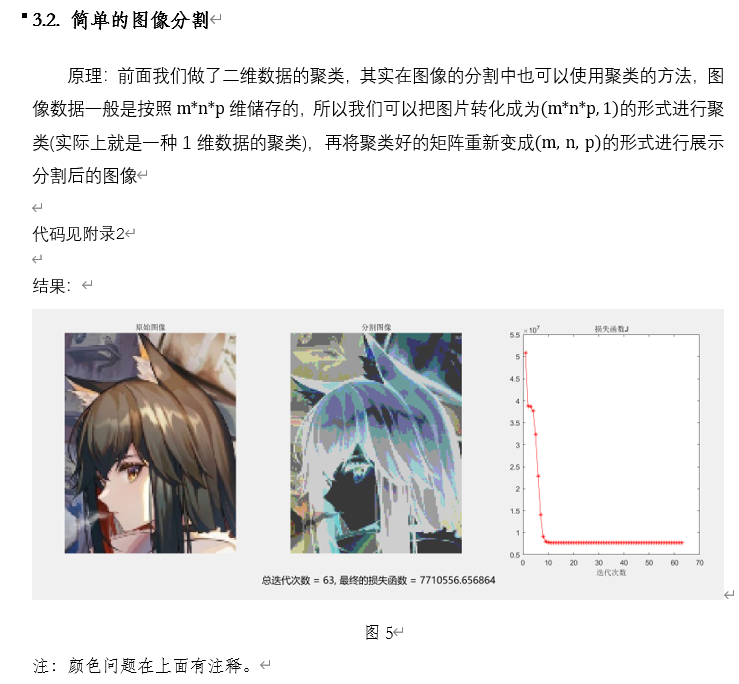
clear clc;
close all;
img = double(imread('texas.png'));
subplot(1,3,1),imshow(uint8(img));
title('原始图像');
[m,n,p] = size(img);
data = reshape(img, m*n*p,1);%将图像变为1维
[center,U,fcn_J] = fcm1(data,4); %分4类
[~,label] = max(U); % 找到所属的类
img_new = reshape(label,size(img)); % 类别还原成原来的图像

subplot(1,3,2),imshow(uint8(img_new.*-50.+256)); % 此处最后图像的着色存在问题imshow(img,[])好像跑不出来想要的效果
title('分割图像');
subplot(1,3,3),plot(fcn_J,'r-*');
title('损失函数J');
set(gca,'position',[0.7 0.234 0.22 0.56]); %设置位置
xlabel('迭代次数');

function [center, U, fcn_J] = fcm1(data, cluster_n, options)

if nargin ~= 2 && nargin ~= 3   %判断函数输入变量
    error('输入变量的数量不对');
end

default_options = [2; 200; 1e-5; 1];%设定默认值
%分别是平滑因子，迭代次数，收敛标准，是否显示迭代过程(0为否，1为是)

if nargin == 2     %使用默认值
    options = default_options;
else
    if length(options) < 4   %options中变量输入正确
        tmp = default_options;
        tmp(1:length(options)) = options;
        options = tmp;
    end
    % 将options中为nan的变量用默认值替代
    nan_index = find(isnan(options)==1);
    options(nan_index) = default_options(nan_index);
    if options(1) <= 1 %判断分类数是否大于等于1
        error('分类数需要大于等于1！');
    end
end

data_n = size(data, 1);     %样本数量
data_d = size(data, 2);     %样本维度

expo = options(1);            % 平滑因子
max_iter = options(2);        % 最大迭代次数
min_criteria = options(3);  % 收敛标准
display = options(4);        % 是否显示迭代过程

fcn_J = zeros(max_iter, 1);            % 初始化损失函数

% 随机初始化隶属度矩阵U
U = rand(cluster_n, data_n);
col_sum = sum(U);
U = U./col_sum(ones(cluster_n, 1), :);    

%迭代
for i = 1:max_iter
    mf = U.^expo;           % 平滑处理m，隶属度矩阵中每个数据乘以次方
    center = mf*data./(sum(mf,2)*ones(1,size(data,2)));   % 更新新的中心,式子(7)
    % 其中data = [x1';x2';...;xj']
    % sum(mf,2)表示按照行相加，得到[sum_mf1;sum_mf2;...;sum_mfi]
    % sum(mf,2)*ones(1,size(data,2),即为i*1与1*i矩阵相乘得到i*i

    dist = distfcm1(center, data);       % 计算欧式距离
    % dist = [||c1-x1||,...,||c1-xj||;...;||ci-x1||,...,||ci-xj||]
    fcn_J(i) = sum(sum((dist.^2).*mf));  % 计算损失函数J
    % 两个sum第一个是先加i，得到[sum1,sum2,...,sumj]
    % 第二个sum再把j加起来

     % 更新新的隶属度矩阵，式子(6)
    tmp = dist.^(-2/(expo-1));     % ||ci-xj||^(-2/(m-1))
    U = tmp./(ones(cluster_n, 1)*sum(tmp)); % 式子(6),进行更新
    
    if display 
        fprintf('迭代次数 = %d, 损失函数 = %f\n', i, fcn_J(i));
    end
    
    % 判断是否收敛
    if i > 1
        if abs(fcn_J(i) - fcn_J(i-1)) < min_criteria
            break; 
        end
    end
end
fprintf('总迭代次数 = %d, 最终的损失函数 = %f\n', i, fcn_J(i));
fcn_J(i+1:max_iter) = []; % 将未迭代的矩阵空间变为空
end


function out = distfcm1(center, data)%计算欧式距离
out = zeros(size(center, 1), size(data, 1));
for k = 1:size(center, 1)
    out(k, :) = sqrt(sum(((data-ones(size(data, 1), 1)*center(k, :)).^2), 2)); 
    %分别计算所有点到第k类的距离
end
end

 

 

 

 

 

 

 

 

参考资料

[1] 模糊集理论 于洪 http://cs2.cqupt.edu.cn/yuhong/

[2] 统计学习方法(第2版) 李航 2012.9

[3] 公式推导视频代码借鉴链接：http://www.powercam.cc/slide/20878

[4] 公式推导代码借鉴文字版：https://blog.csdn.net/on2way/article/details/47087201

[5] C-means算法原理：https://blog.csdn.net/wzl1997/article/details/79264560?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

[6] 一种改进的FCM聚类算法的混合矩阵估计 郭凌飞，张林波 应用科技 2019.3

[7] MATLAB函数fcm源代码