HOG特征(代码实现)
HOG特征
方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来构成特征。Hog特征结合SVM分类器已经被广泛应用于图像识别中,尤其在行人检测中获得了极大的成功。需要提醒的是,HOG+SVM进行行人检测的方法是法国研究人员Dalal在2005的CVPR上提出的,而如今虽然有很多行人检测算法不断提出,但基本都是以HOG+SVM的思路为主。
(1)主要思想:
在一副图像中,局部目标的表象和形状(appearance and shape)能够被梯度或边缘的方向密度分布很好地描述。(本质:梯度的统计信息,而梯度主要存在于边缘的地方)。
(2)具体的实现方法是:
首先将图像分成小的连通区域,我们把它叫细胞单元。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。
(3)提高性能:
把这些局部直方图在图像的更大的范围内(我们把它叫区间或block)进行对比度归一化(contrast-normalized),所采用的方法是:先计算各直方图在这个区间(block)中的密度,然后根据这个密度对区间中的各个细胞单元做归一化。通过这个归一化后,能对光照变化和阴影获得更好的效果。
(4)优点:
与其他的特征描述方法相比,HOG有很多优点。首先,由于HOG是在图像的局部方格单元上操作,所以它对图像几何的和光学的形变都能保持很好的不变性,这两种形变只会出现在更大的空间领域上。其次,在粗的空域抽样、精细的方向抽样以及较强的局部光学归一化等条件下,只要行人大体上能够保持直立的姿势,可以容许行人有一些细微的肢体动作,这些细微的动作可以被忽略而不影响检测效果。因此HOG特征是特别适合于做图像中的人体检测的。
HOG特征提取算法的实现过程
HOG特征提取方法就是将一个image(你要检测的目标或者扫描窗口):
1)灰度化(将图像看做一个x,y,z(灰度)的三维图像);
2)采用Gamma校正法对输入图像进行颜色空间的标准化(归一化);目的是调节图像的对比度,降低图像局部的阴影和光照变化所造成的影响,同时可以抑制噪音的干扰;
3)计算图像每个像素的梯度(包括大小和方向);主要是为了捕获轮廓信息,同时进一步弱化光照的干扰。
4)将图像划分成小cells(例如8*8像素/cell);
5)统计每个cell的梯度直方图(不同梯度的个数),即可形成每个cell的descriptor;
6)将每几个cell组成一个block(例如2*2个cell/block),一个block内所有cell的特征descriptor串联起来便得到该block的HOG特征descriptor。
7)将图像image内的所有block的HOG特征descriptor串联起来就可以得到该image(你要检测的目标)的HOG特征descriptor了。这个就是最终的可供分类使用的特征向量了。
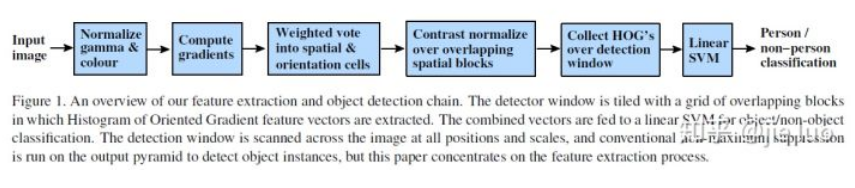
具体每一步的详细过程
(1)标准化gamma空间和颜色空间(包括伽马校正和灰度化。这是可选的步骤,因为实验证明做不做影响不大)
为了减少光照因素的影响,首先需要将整个图像进行规范化(归一化)。在图像的纹理强度中,局部的表层曝光贡献的比重较大,所以,这种压缩处理能够有效地降低图像局部的阴影和光照变化。因为颜色信息作用不大,通常先转化为灰度图;
Gamma压缩公式:
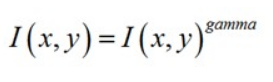
比如可以取Gamma=1/2;
(2)计算图像梯度
计算图像横坐标和纵坐标方向的梯度,并据此计算每个像素位置的梯度方向值;求导操作不仅能够捕获轮廓,人影和一些纹理信息,还能进一步弱化光照的影响。
图像中像素点(x,y)的梯度为:

最常用的方法是:首先用[-1,0,1]梯度算子对原图像做卷积运算,得到x方向(水平方向,以向右为正方向)的梯度分量gradscalx,然后用[1,0,-1]T梯度算子对原图像做卷积运算,得到y方向(竖直方向,以向上为正方向)的梯度分量gradscaly。然后再用以上公式计算该像素点的梯度大小和方向。

代码:
# Python gradient calculation # Read image im = cv2.imread('bolt.png') im = np.float32(im) / 255.0 # Calculate gradient gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)#水平 gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)#垂直
# Python Calculate gradient magnitude and direction ( in degrees ) mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
(3)为每个细胞单元构建梯度方向直方图
按照第二步的计算,每一个像素点都会有两个值:梯度强度/梯度方向。
现在就计算梯度直方图,这是一个关键步骤也是HOG能够work的原因。
梯度直方图是在一个8*8的cell里面计算的。那么在8*8的cell里面就会有8*8*2=128个值,2是包括了梯度强度和梯度方向。通过统计形成梯度直方图,128个值将会变成9个值,大大降低了计算量,同时又对光照等环境变化更加地robust。
首先,我将0-180度分成9个bins,分别是0,20,40...160。然后统计每一个像素点所在的bin。请看下图:
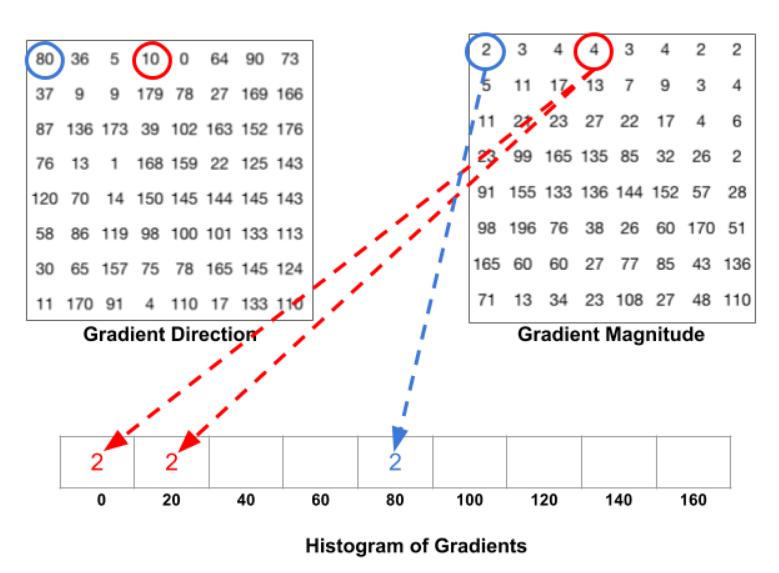
左上图是8*8的梯度方向值,右上图是8*8的梯度强度值,下图是9个bins。
先看两个蓝色圈圈。因为蓝圈的方向是80度,大小是2,所以该点就投给80这个bin;
再看两个红色圈圈。因为红色圈圈的方向是10,大小是4,因为10距离0点为10,距离20点为也为10,那么有一半的大小是投给0这个bin,还有一半的大小(即是2)投给20这个bin。

如果该角度大于160度,则该角度在160到180之间,我们知道该角度将使0和180相等。因此,在下面的示例中,角度为165度的像素对0度仓bin和160度bin成比例地贡献。
那么统计完64个点的投票数以后,每个bin就会得到一个数值,可以得到一个直方图,在计算机里面就是一个大小为9的数组。
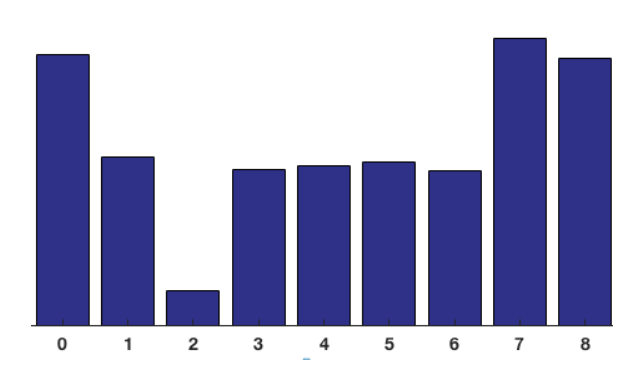
从上图可以看到,更多的点的梯度方向是倾向于0度和160度,也就是说这些点的梯度方向是向上或者向下,表明图像这个位置存在比较明显的横向边缘。因此HOG是对边角敏感的,由于这样的统计方法,也是对部分像素值变化不敏感的,所以能够适应不同的环境。
(4)把细胞单元组合成大的块(block),块内归一化梯度直方图
由于局部光照的变化以及前景-背景对比度的变化,使得梯度强度的变化范围非常大。这就需要对梯度强度做归一化。归一化能够进一步地对光照、阴影和边缘进行压缩。
归一化的方法是向量的每一个值除以向量的模长:
比如对于一个(128,64,32)的三维向量来说,模长是 , 那么归一化后的向量变成了(0.87,0.43,0.22)
那么16*16大小的block是怎么来的?见动图:gif
在计算HOG时,您可以像对上述3×1向量进行归一化一样简单地对9×1直方图进行归一化。这不是一个坏主意,但是更好的主意是对更大的16×16块进行标准化(绿色方块是8*8大小的cell,蓝色方块就是由4个cell组成的block)。16×16块具有4个直方图,可以将它们连接起来以形成36 x 1元素向量,并且可以像对3×1向量进行归一化的方式对其进行归一化。然后将窗口移动8个像素(请参见动画gif),并在此窗口上计算归一化的36×1向量,并重复该过程。
作者采取的办法就是如上所述:把各个细胞单元组合成大的、空间上连通的区间(blocks)。这样,一个block内所有cell的特征向量串联起来便得到该block的HOG特征。这些区间是互有重叠的,这就意味着:每一个单元格的特征会以不同的结果多次出现在最后的特征向量中。我们将归一化之后的块描述符(向量)就称之为HOG描述符。
(5)计算HOG特征向量
每一个16*16大小的block将会得到36大小的vector。那么对于一个64*128大小的图像,按照上图的方式提取block,将会有7个水平位置和15个竖直位可以取得,所以一共有7*15=105个block,所以我们整合所有block的vector,形成一个大的一维vector的大小将会是36*105=3780。
代码
import cv2 import numpy as np import math import matplotlib.pyplot as plt class Hog_descriptor(): #HOG描述符 ''' bin_size:直方图的bin个数 构造函数 默认参数,一个block由2x2个cell组成,步长为1个cell大小 args: img:输入图像(更准确的说是检测窗口),这里要求为灰度图像 对于行人检测图像大小一般为128x64 即是输入图像上的一小块裁切区域 cell_size:细胞单元的大小 如8 ''' def __init__(self, img, cell_size=8, bin_size=9): self.img = img ''' 伽马校正 self.img = np.sqrt(img / np.max(img)) self.img = img * 255 ''' self.cell_size = cell_size self.bin_size = bin_size self.angle_unit = 360 / self.bin_size #对于360的迷惑 def extract(self): height, width = self.img.shape #1.计算每个像素的梯度和方向 gradient_magnitude, gradient_angle = self._global_gradient() gradient_magnitude = abs(gradient_magnitude) cell_gradient_vector = np.zeros((height // self.cell_size, width // self.cell_size, self.bin_size)) for i in range(cell_gradient_vector.shape[0]): for j in range(cell_gradient_vector.shape[1]): #取一个cell中的梯度大小和方向 cell_magnitude = gradient_magnitude[i * self.cell_size:(i + 1) * self.cell_size, j * self.cell_size:(j + 1) * self.cell_size] cell_angle = gradient_angle[i * self.cell_size:(i + 1) * self.cell_size, j * self.cell_size:(j + 1) * self.cell_size] #得到每一个cell的梯度直方图; cell_gradient_vector[i][j] = self._cell_gradient(cell_magnitude, cell_angle) #得到HOG特征可视化图像 hog_image = self._render_gradient(np.zeros([height, width]), cell_gradient_vector) #HOG特征向量 hog_vector = [] #使用滑动窗口 for i in range(cell_gradient_vector.shape[0] - 1): for j in range(cell_gradient_vector.shape[1] - 1): #4个cell得到一个block block_vector = cell_gradient_vector[i:i+1][j:j+1].reshape(-1, 1)#串联 #正则化 block_vector = np.array([vector / np.linalg.norm(vector) for vector in block_vector]) hog_vector.append(block_vector) return hog_vector, hog_image def _global_gradient(self): #得到每个像素的梯度 gradient_values_x = cv2.Sobel(self.img, cv2.CV_64F, 1, 0, ksize=5)#水平 gradient_values_y = cv2.Sobel(self.img, cv2.CV_64F, 0, 1, ksize=5)#垂直 gradient_magnitude = np.sqrt(gradient_values_x**2 + gradient_values_y**2)#总 gradient_angle = cv2.phase(gradient_values_x, gradient_values_y, angleInDegrees=True)#方向 return gradient_magnitude, gradient_angle def _cell_gradient(self, cell_magnitude, cell_angle): #得到cell的梯度直方图 orientation_centers = [0] * self.bin_size for i in range(cell_magnitude.shape[0]): for j in range(cell_magnitude.shape[1]): gradient_strength = cell_magnitude[i][j] gradient_angle = cell_angle[i][j] min_angle, max_angle, mod = self._get_closest_bins(gradient_angle) orientation_centers[min_angle] += (gradient_strength * (1 - (mod / self.angle_unit))) orientation_centers[max_angle] += (gradient_strength * (mod / self.angle_unit)) return orientation_centers def _get_closest_bins(self, gradient_angle): idx = int(gradient_angle / self.angle_unit) mod = gradient_angle % self.angle_unit #return :起始bin索引,终止bin的索引,end索引对应bin所占权重 return idx, (idx + 1) % self.bin_size, mod def _render_gradient(self, image, cell_gradient): #得到HOG特征图 cell_width = self.cell_size / 2 max_mag = np.array(cell_gradient).max() for x in range(cell_gradient.shape[0]): for y in range(cell_gradient.shape[1]): cell_grad = cell_gradient[x][y] cell_grad /= max_mag #归一化 angle = 0 angle_gap = self.angle_unit for magnitude in cell_grad: # 转换为弧度 angle_radian = math.radians(angle) # 计算起始坐标和终点坐标,长度为幅值(归一化),幅值越大、绘制的线条越长、越亮 x1 = int(x * self.cell_size + magnitude * cell_width * math.cos(angle_radian)) y1 = int(y * self.cell_size + magnitude * cell_width * math.sin(angle_radian)) x2 = int(x * self.cell_size - magnitude * cell_width * math.cos(angle_radian)) y2 = int(y * self.cell_size - magnitude * cell_width * math.sin(angle_radian)) cv2.line(image, (y1, x1), (y2, x2), int(255 * math.sqrt(magnitude))) angle += angle_gap return image img = cv2.imread('C:/Users/shishenhao/Desktop/tt.png', cv2.IMREAD_GRAYSCALE) # 灰度图片 hog = Hog_descriptor(img, cell_size=8, bin_size=9) vector, image = hog.extract() print(np.array(vector).shape) plt.subplot(121) plt.imshow(img, cmap=plt.cm.gray) plt.subplot(122) plt.imshow(image, cmap=plt.cm.gray) plt.show()
结果:

参考
https://www.cnblogs.com/zyly/p/9651261.html#_label4
https://blog.csdn.net/ppp8300885/article/details/71078555
https://blog.csdn.net/zouxy09/article/details/7929348
https://www.learnopencv.com/histogram-of-oriented-gradients/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号