统计学习方法第四章课后作业(dirichlet分布,朴素贝叶斯多项式模型)
4.1证明如下两个式子
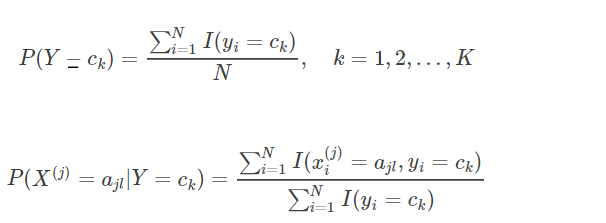
首先先要明确极大似然估计是频率派的主张,本质上看的是频率。
证明:
![]()
其中M表示的就是 Y = ck 发生的次数, N就是独立同分布随机抽取的样本数
所以得到概率:
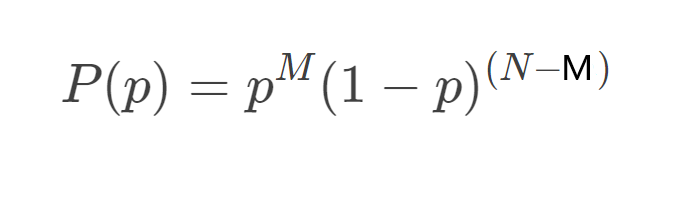
极大似然估计,两边取对数:
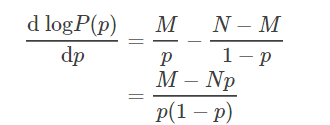
上式等于0,得到:
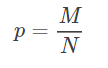
即证明。(感觉有点点熟悉这是什么)
之后同理可以得到:
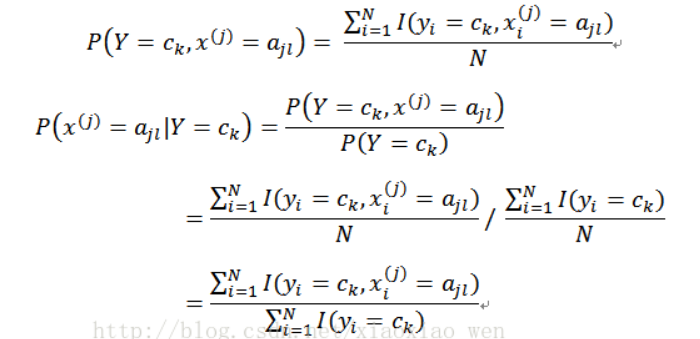
4. 2
证明:
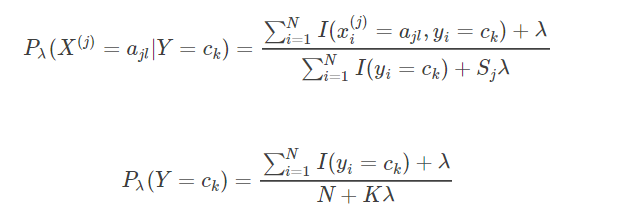
先证明下一个公式
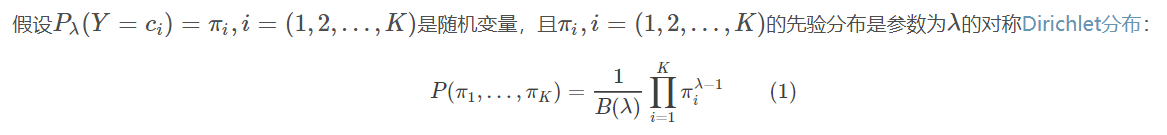
注: 其中Dirichlet分布与beta分布有所关联,beta分布式一种二项的分布,而dirichlet分布是一种多项的分布又称为多项beta分布,如下所示
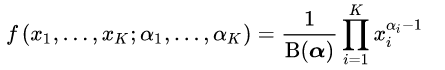
而对称dirichlet分布是:
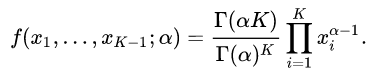

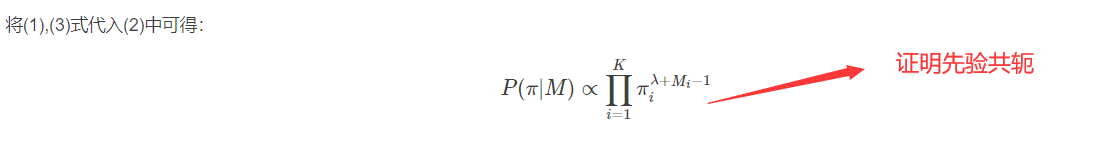
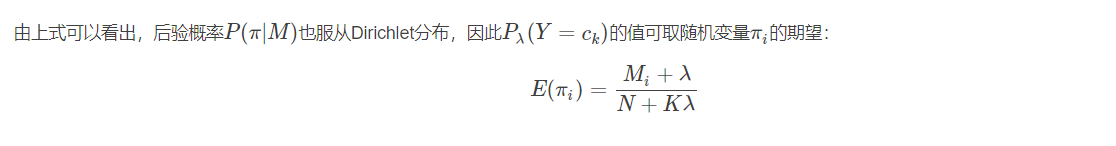
当数据多可以取期望:
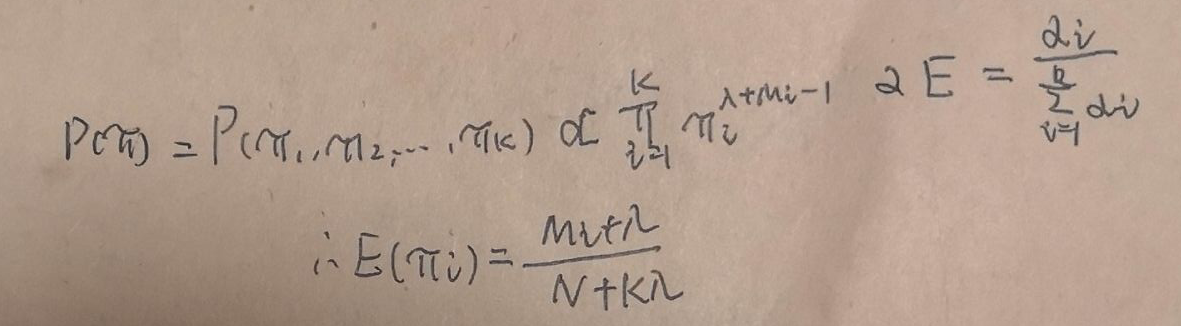
同理可得:
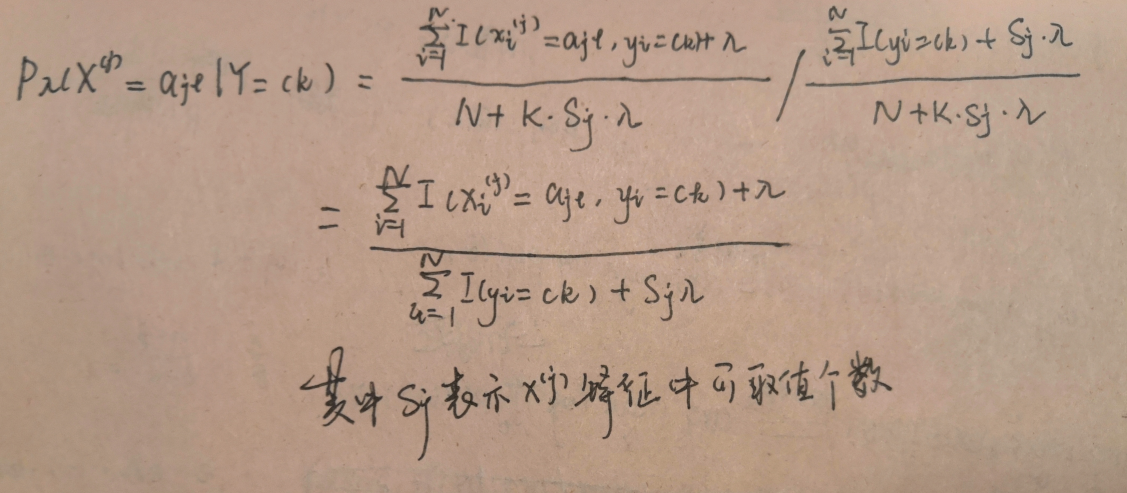
另一种推理方法:

该解法:
1.关于贝叶斯估计那一块,是从MAP角度推导的,并不是贝叶斯估计,看起来结果一样是因为共轭分布的关系.
2.关于均匀分布的参数λ解释太粗略.均匀分布其实是服从参数λ为1的Dirichlet分布,书里的意思应该是服从Dirichlet先验,只是当λ为1(即拉普拉斯平滑)时,等于服从均匀分布,把λ当做均匀分布的参数看起来有点因果倒置
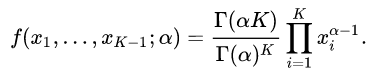
因为是对称的dirichlet分布, 所以当α = 1 ,对称Dirichlet分布等效于开放标准(K -1)-单纯形上的均匀分布,即在其支持的所有点上均匀。这种特殊的分布称为平面Dirichlet分布。浓度参数的值大于1时,倾向于使用密集,均匀分布的变量,即,单个样本中的所有值彼此相似。低于1的浓度参数值倾向于稀疏分布,即,单个样本中的大多数值将接近于0,并且大部分质量将集中在少数几个值中。
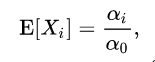
又因为上图
![]()
对于下图的解释是,当λ=0时,即没有先验概率,就是极大似然估计,λ可以任取
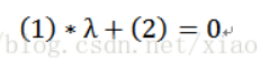
朴素贝叶斯多项式模型代码:
import numpy as np
class MultinomialNB(object):
"""
朴素贝叶斯分类器用于多项模型
多项式朴素贝叶斯分类器适用于使用离散特征
参数
----------
alpha:浮点型,可选(默认= 1.0)
设置alpha = 0不进行平滑
设置0 <alpha <1称为Lidstone平滑
设置alpha = 1称为拉普拉斯平滑
fit_prior:boolean
是否学习类中的先验概率。
如果为False,将使用统一的先验,即全部相等的先验。
class_prior:类数组的大小(n_classes,)
该类的先验概率。如果指定,则先验条件不根据数据进行调整。
属性
----------
fit(X,y):
X和y类似于数组,表示要素和标签。
调用fit()方法来训练朴素贝叶斯分类器。
predict(X):
"""
def __init__(self, alpha = 1.0, fit_prior=True, class_prior=None):
self.alpha = alpha
self.fit_prior = fit_prior
self.class_prior = class_prior
self.classes = None
self.conditional_prob = None
def _calculate_feature_prob(self, feature):
values = np.unique(feature) #特征中的可取值
total_num = float(len(feature)) #计算特征数量
value_prob = {} #存放计算后的可取值的概率
for v in values:
value_prob[v] = ((np.sum(np.equal(feature, v)) + self.alpha) / (total_num + len(values) * self.alpha))
return value_prob
def fit(self, X, y):
#TODO:check X,y
self.classes = np.unique(y) #类型中的可取值
#计算先验概率P(y=ck)
if self.class_prior == None: #如果类中没有先验概率
class_num = len(self.classes)
if not self.fit_prior: #如果不使用先验概率
self.class_prior = [1.0/class_num for _ in range(class_num)] #统一化处理,概率都相同
else:
self.class_prior = []
sample_num = float(len(y)) #y中数量总数
for c in self.classes: #计算每个类型的概率
self.class_prior.append((np.sum(np.equal(y, c))+ self.alpha) / (sample_num + class_num * self.alpha))
#计算条件概率 P( xj | y=ck )
self.conditional_prob = {} # 形如{ c0:{ x0:{ value0:0.2, value1:0.8 }, x1:{} }, c1:{...} }
for c in self.classes: #遍历类型
self.conditional_prob[c] = {}
for i in range(len(X[0])): #特征个数
feature = X[np.equal(y, c)][:, i] #提取同个类型的特征
self.conditional_prob[c][i] = self._calculate_feature_prob(feature) #计算某个类型的某种特征的某种取值的概率
return self
#返回目标值,value_prob形如{value0:0.2, value1:0.1,value3:0.3,.. }
def _get_xj_prob(self, value_prob, target_value):
return value_prob[target_value]
#进行一个样本预测,基于先验概率和条件概率
def _predict_single_sample(self, x): #先验概率 * 条件概率 / 常数 = 后验概率
label = -1 #类型
max_posterior_prob = 0 #最大概率
for c_index in range(len(self.classes)):
current_class_prior = self.class_prior[c_index] #当前类型的概率
current_conditional_prob = 1.0 #当前的条件概率
feature_prob = self.conditional_prob[self.classes[c_index]] #当前类型的各个特征的概率,形如{x0:{ value0:0.2, value1:0.8 };x1:{}}
j = 0
for feature_i in feature_prob.keys(): #遍历每个特征的某种特定概率
current_conditional_prob *= self._get_xj_prob(feature_prob[feature_i], x[j]) #x表示指定的各个特征中的某个值,array,j是特征xj中的j
j += 1
if current_class_prior * current_conditional_prob > max_posterior_prob: #跟新最大的概率与类型
max_posterior_prob = current_class_prior * current_conditional_prob
label = self.classes[c_index]
return label
def predict(self, X): #X代表输入的特定样本
if X.ndim == 1: #数组X的维度为1
return self._predict_single_sample(X)
else:
#各种样本
labels = []
for i in range(X.shape[0]):
label = self._predict_single_sample(X[i])
labels.append(label)
return labels
X = np.array([
[1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],
[4,5,5,4,4,4,5,5,6,6,6,5,5,6,6]
])
X = X.T
y = np.array([-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
nb = MultinomialNB(alpha=1.0,fit_prior=True)
nb.fit(X,y)
print(nb.predict(np.array([[2,4],[1,5]])))
参考
from https://blog.csdn.net/bumingqiu/article/details/73397812
https://blog.csdn.net/xiaoxiao_wen/article/details/54097917
dirichlet分布:https://en.wikipedia.org/wiki/Dirichlet_distribution
代码参考:https://blog.csdn.net/u012162613/article/details/48323777


 浙公网安备 33010602011771号
浙公网安备 33010602011771号