【数据结构与算法Python版学习笔记】图——强连通分支

互联网

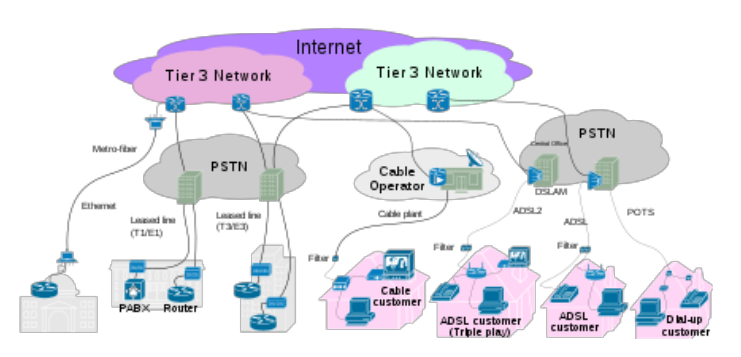
我们关注一下互联网相关的非常巨大图：

• 由主机通过网线（或无线）连接而形成的图；
• 以及由网页通过超链接连接而形成的图。

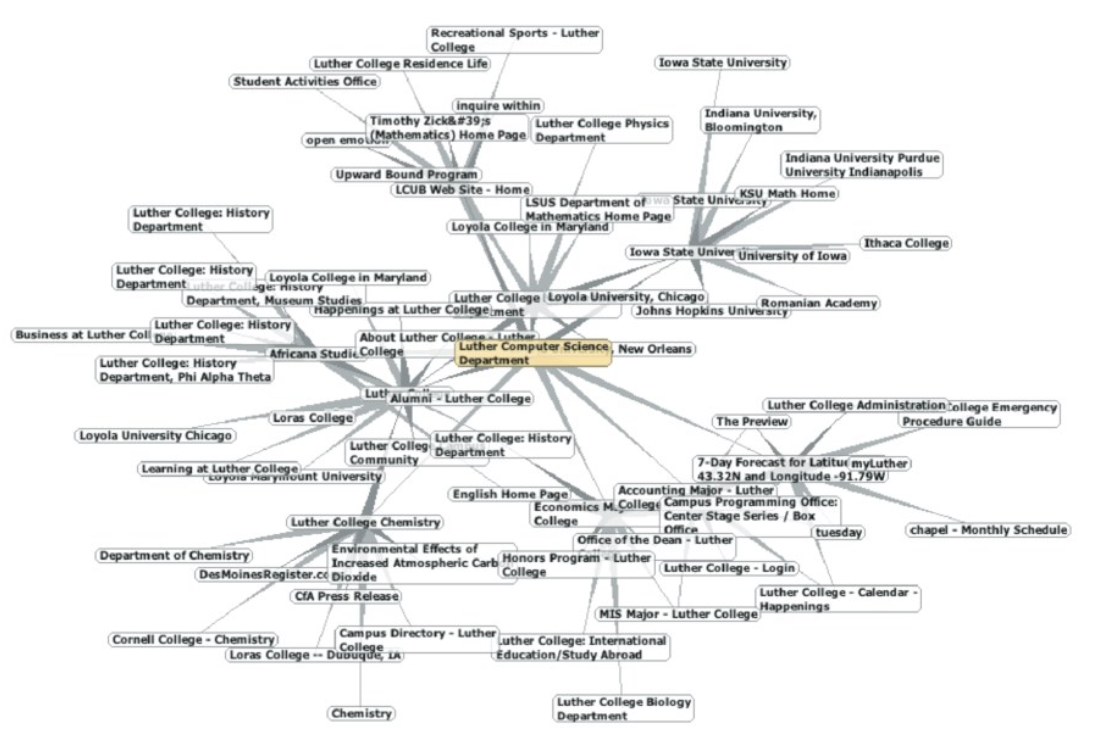
网页形成的图

• 以网页（URI作为id）为顶点，网页内包含的超链接作为边，可以转换为一个有向图。
• 得出这样的结论：网络具有一种基础结构，使得在某种程度上相似的网页相互聚集。

---

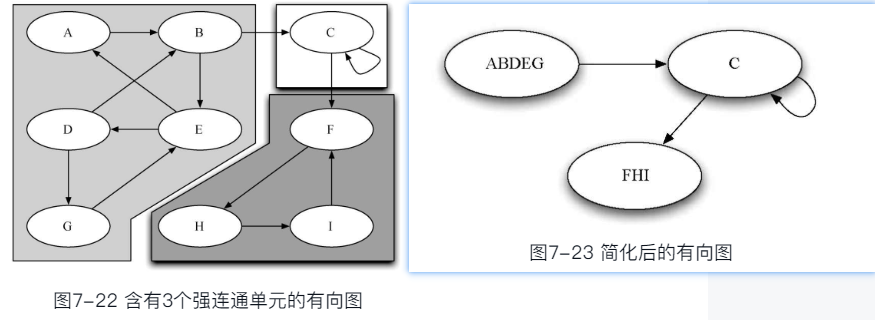
强连通分支Strongly Connected Components

概念

• 通过一种叫作强连通分支的图算法，可以找出图中高度连通的顶点簇(发现高度聚集节点群)。
• 强连通分支，定义为图G的一个子集C
  • C中的任意两个顶点v,w之间都有路径来回，即(v,w)(w,v)都是C的路径，
  • 而且C是具有这样性质的最大子集

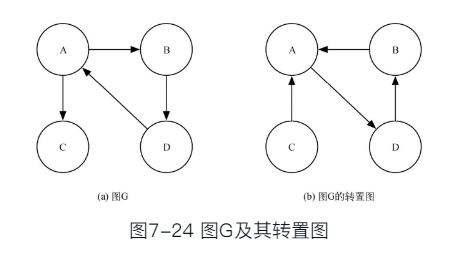
转置 Transposition

在用深度优先搜索来发现强连通分支之前， 先熟悉一个概念： Transposition转置

• 一个有向图G的转置GT，定义为将图G的所有边的顶点交换次序，如将(v,w)转换为(w,v)
• 可以观察到图和转置图在强连通分支的数量和划分上，是相同的。

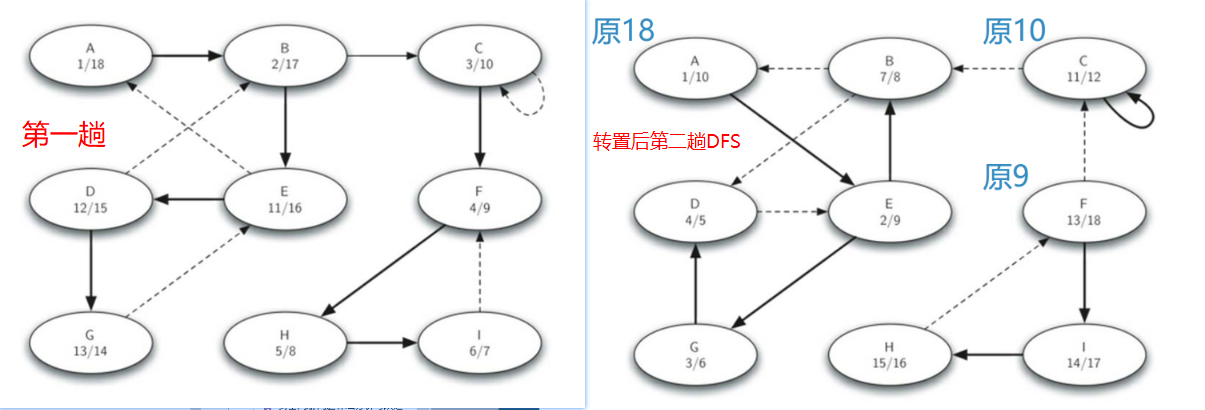
强连通分支算法： Kosaraju算法思路

• 首先， 对图G调用DFS算法， 为每个顶点计算“结束时间”；
• 然后， 将图G进行转置， 得到$G^T$；
• 再对$G^T$调用DFS算法， 但在dfs函数中，对每个顶点的搜索循环里， 要以顶点的“结束时间”倒序的顺序来搜索
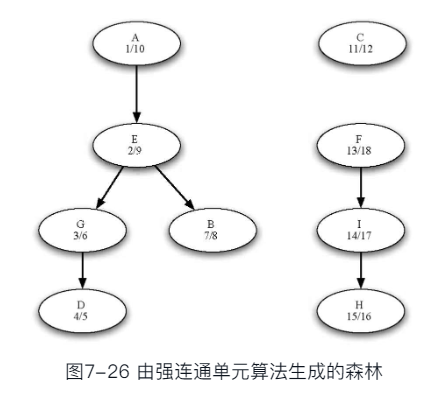
• 最后， 深度优先森林中的每一棵树就是一个强连通分支

另外的常用强连通分支算法

• Tarjan算法
• Gabow算法，对Tarjan的改进