【数据结构与算法Python版学习笔记】图——基本概念及相关术语

概念

• 图Graph是比树更为一般的结构， 也是由节点和边构成
  实际上树是一种具有特殊性质的图
• 图可以用来表示现实世界中很多有意思的事物，包括道路系统、城市之间的航班、互联网的连接，甚至是计算机专业的一系列必修课

定义

• 一个图G可以定义为G=(V, E)
  • 其中V是顶点的集合， E是边的集合， E中的每条边e=(v, w)， v和w都是V中的顶点；
  • 如果是赋权图，则可以在e中添加权重分量子图： V和E的子集

术语表

• 顶点Vertex（也称“节点Node”）
  是图的基本组成部分，顶点具有名称标识Key，也可以携带数据项payload

• 边Edge（也称“弧Arc”）
  作为2个顶点之间关系的表示，边连接两个顶点；

• 边
  可以是无向或者有向的，相应的图称作“无向图”和“有向图”

• 权重Weight
  为了表达从一个顶点到另一个顶点的“代价”，可以给边赋权；例如公交网络中两个站点之间的“距离”、“通行时间”和“票价”都可以作为权重
  

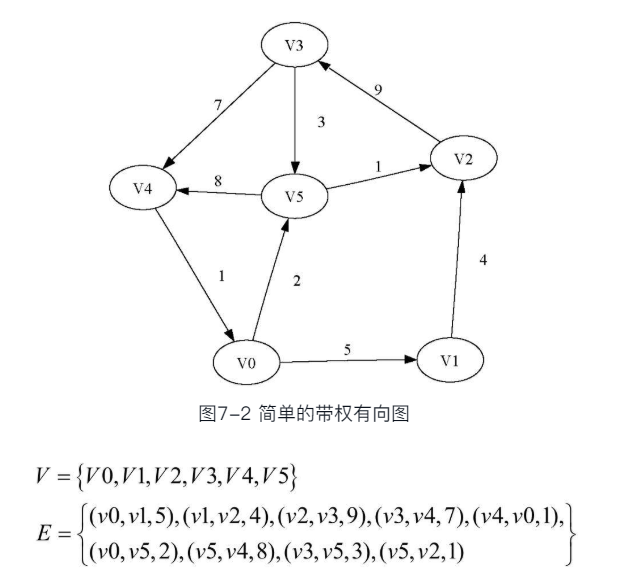
• 路径Path
  图中的路径，是由边依次连接起来的顶点序列；无权路径的长度为边的数量；带权路径的长度为所有边权重的和；

• 环（圈Cycle）

  • 环是有向图中的一条起点和终点为同一个顶点的路径。
  • 没有环的图被称为无环图，没有环的有向图被称为有向无环图，简称为DAG

---

图的抽象数据类型

• Graph()新建一个空图。

• addVertex(vert)向图中添加一个顶点实例。

• addEdge(fromVert, toVert)向图中添加一条有向边，用于连接顶点fromVert和toVert。

• addEdge(fromVert, toVert, weight)向图中添加一条带权重weight的有向边，用于连接顶点fromVert和toVert。

• getVertex(vertKey)在图中找到名为vertKey的顶点。

• getVertices()以列表形式返回图中所有顶点。

• in通过vertex in graph这样的语句，在顶点存在时返回True，否则返回False。

实现方法

• 邻接矩阵adjacency matrix
• 邻接表adjacency list

两种方法各有优劣，需要在不同应用中加以选择

邻接矩阵Adjacency Matrix

• 矩阵的每行和每列都代表图中的顶点
• 如果两个顶点之间有边相连， 设定行列值
  • 无权边则将矩阵分量标注为1，或者0
  • 带权边则将权重保存为矩阵分量值
• 优点是简单，可以很容易得到顶点是如何相连
• 但如果图中的边数很少则效率低下
  成为“稀疏sparse”矩阵，而大多数问题所对应的图都是稀疏的

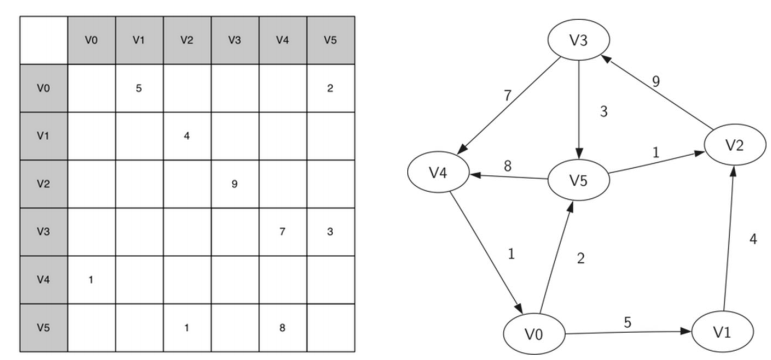
邻接列表Adjacency List

• 邻接列表adjacency list可以成为稀疏图的更高效实现方案
  • 维护一个包含所有顶点的主列表（master list）
  • 主列表中的每个顶点，再关联一个与自身有边连接的所有顶点的列表
• 邻接列表法的存储空间紧凑高效
  很容易获得顶点所连接的所有顶点，以及连接边的信息

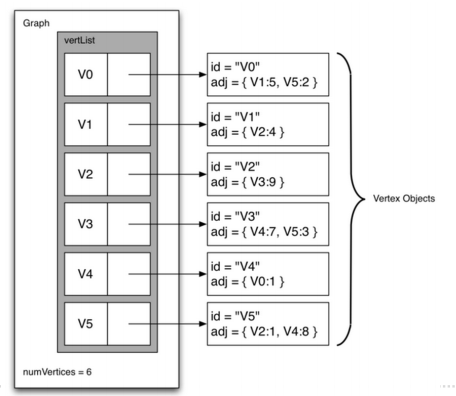
代码

class Vertex:
    def __init__(self, key):
        self.id = key
        self.connectedTo = {}

    def addNeigbor(self, nbr, weight=0):
        '''nbr是顶点对象的key'''
        self.connectedTo[nbr] = weight

    def __str__(self):
        return str(self.id)+' connectedTo: ' + str([x.id for x in self.connectedTo])

    def getConnections(self):
        return self.connectedTo.keys()

    def getId(self):
        return self.id

    def getWeight(self, nbr):
        return self.connectedTo[nbr]

class Graph:
    def __init__(self):
        self.vertList = {}
        self.numVertices = 0

    def addVertex(self, key):
        self.numVertices += 1
        newVertex = Vertex(key)
        self.vertList[key] = newVertex
        return newVertex

    def getVertex(self, key):
        if key in self.vertList:
            return self.vertList[key]
        else:
            return None

    def __contains__(self, key):
        return key in self.vertList

    def addEdge(self, f, t, cost=0):
        # 不存在的点先添加
        if f not in self.vertList:
            nv = self.addVertex(f)
        if t not in self.vertList:
            nv = self.addVertex(t)
        # 调用起始顶点的方法添加邻接边
        self.vertList[f].addNeigbor(self.vertList[t], cost)

    def getVertices(self):
        return self.vertList.keys()

    def __iter__(self):
        return iter(self.vertList.values())

if __name__ == "__main__":
    g = Graph()
    for i in range(6):
        g.addVertex(i)
        print(g.vertList[i])

    # print(g.vertList)

    g.addEdge(0, 1, 5)
    g.addEdge(0, 5, 2)
    g.addEdge(1, 2, 4)
    g.addEdge(2, 3, 9)
    for v in g:
        for w in v.getConnections():
            print("%s,%s" % (v.getId(), w.getId()))

		for i in range(6):
		        print(g.vertList[i])

>>>
0 connectedTo: []
1 connectedTo: []
2 connectedTo: []
3 connectedTo: []
4 connectedTo: []
5 connectedTo: []
0,1
0,5
1,2
2,3
0 connectedTo: [1, 5]
1 connectedTo: [2]
2 connectedTo: [3]
3 connectedTo: []
4 connectedTo: []
5 connectedTo: []